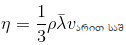m1 იყოს ავსში მოთავსებული აირის მასა. მაშინ
\(p_{1}V=\frac{m_{1}}{M}RT_{1}\)
გაცხელების შემდეგ გაზის რაღაც ნაწილი გადავა მეორე ავზში მანამ სანამ წნევათა შორის სხვაობა არ გახდება ∆p. p'1 და p'2 იყოს წნევები სარქველის აქეთ იქით. მაშინ \(p'_{1}V=\frac{m'_{1}}{M}RT_{1}\) (აქ არის შეცდომა. რადგან ორივე მხარეს გაცხელების მერე ტემპერატურა არის T2, ამიტომ აქ უნდა ეწეროს \(p'_{1}V=\frac{m'_{1}}{M}RT_{2}\). ამის შემდგომ ყველაფერი სწორია) და \(p'_{2}V=\frac{m'_{2}}{M}RT_{2}=\frac{\left (m_{1}-m'_{1} \right )}{M}RT_{2}\) აქედან,
\(p'_{2}=\left (\frac{p_{1}}{T_{1}}-\frac{p'_{1}}{T_{2}} \right )T_{2}\)
გავითვალისწინოთ, რომ \(\Delta p=p'_{1}-p'_{2}\) და გვექნება
\(p'_{2}=p_{1}\frac{T_{2}}{T_{1}}-p'_{2}-\Delta p\) აქედან კი
\(p'_{2}=\frac{1}{2}\left (p_{1}\frac{T_{2}}{T_{1}}-\Delta p \right )\)=0,08 ატმ.
m1 და m2 იყოს აირის მასები აირის გამოშვებამდე და მის შემდეგ შესაბამისად. მაშინ
∆m= m1 - m2
იდეალური გაზის მდგომარეობის განტოლების მიხედვით
\(p_{1}V=\frac{m_{1}}{\mu }RT_{0}\) და \(p_{2}V=\frac{m_{2}}{\mu }RT_{0}\) აქედან
\(\left (p_{1}-p_{1} \right )V=\frac{\left (m_{1}-m_{1} \right )}{\mu }RT_{0}=\Delta m\frac{R}{M}T_{0}\)
საიდანაც
\(\Delta m=\Delta p\frac{MV}{RT_{0}}\) (1)
ასევე ვიცით, რომ
\(\frac{M}{RT_{0}}=\frac{\rho }{p_{0}}\) (2)
სადაც p0 არის სტანდარტული ატმოსფერული წნევა T=273K ტემპერატურაზე.
(1) და (2) განტოლებებიდან მივიღებთ,
\(\Delta m=\rho V\frac{\Delta p}{p_{0}}\)=30გ.
ამოცანა 14.1
V=30 ლიტრიან ჭურჭელში მოთავსებულია 0oC ტემპერატურის იდეალური აირი. მას შემდეგ, რაც ნაწილი აირისა გამოუშვეს გარეთ, ჭურჭელში წნევა შემცირდა \(\Delta p=\)0.78 ატმოსფეროთი (ტემპერატურა დარჩა უცვლელი). იპოვეთ გამოთავისუფლებული აირის მასა. ნორმალურ პირობებში აირის სიმკვრივე არის \(\rho =\)1.3გ/ლ. (იროდოვი 2.1)
ამოცანა 14.2
ორი ერთნაირი ავზი დაკავშირებულია სარქველიანი მილით, რომელიც ავზებს შორის ატარებს აირს თუ მათ წნევათა შორის სხვაობა \(\Delta p\geqslant\)1,10 ატმოსფეროზე. თავდაპირველად ერთ ავზში იყო ვაკუუმი, როცა მეორეში იყო \(p_{1}=\) 1.00ატმ წნევისა და \(t_{1}=\) 27oC ტემპერატურის მქონე იდეალური აირი. შემდეგ ორივე ავზი გააცხელეს 107oC ტემპერატურამდე. რა სიდიდემდე გაიზრდება წნევა თავდაპირველად ვაკუუმიან ავზში? (იროდოვი 2.2)
ამოცანა 14.3
V=20 ლიტრიან ავზში მოთავსებულია წყალბადისა და ჰელიუმის ნაზავი, რომლის ტემპერატურაა \(t_{1}=\) 20oC და წნევა კი \(p=\) 2 ატმ. ნაზავის მასაა m= 5.0გ. იპოვეთ წყალბადისა და ჰელიუმის მასების თანაფარდობა ამ ნაზავში. (იროდოვი 2.3)
ამოცანა 14.4
ავზში მოთავსებულია აზოტისა (m1 = 7.0 გ) და ნახშირორჯანგის (m2 = 11 გ) ნაზავი T = 290 K ტემპერატურაზე და p0 = 1.0 ატმ წნევაზე. ნაზავი ჩათვალეთ იდეალურ აირად და იპოვეთ მისი სიმკვრივე. (იროდოვი 2.4)
ამოცანა 14.5
ვერტიკალური ავზი დახურულია ორივე ბოლოდან და აქვს ადვილად მოძრავი დგუში, რომელიც ავზს ყოფს ორ ნაწილად. თითოეულ ნაწილში არის თითო მოლი აირი. წონასწორულ მდგომარეობაში To = 300 K ტემპერატურაზე ავზის ზედა ნაწილის მოცულობა 4-ჯერ აღემატება ქვედა ნაწილის მოცულობას. რა ტემპერატურაზე იქნება მათი მოცულობების ფარდობა 3-ის ტოლი? (იროდოვი 2.6)
ამოცანა 14.6
ხდება V მოცულობის ავზის ამოტუმბვა დგუშიანი ტუმბოთი. დგუშის ერთი ამოქაჩვა იტაცებს ∆V მოცულობას. დგუშის რამდენი ამოქაჩვა არის საჭირო, რომ ავზში შემცირდეს წნევა η-ჯერ. იგულისხმება, რომ პროცესი იზოთერმულია და აირი იდეალური. (იროდოვი 2.7)
ამოცანა 14.7
იპოვეთ აირის წნევა როგორც t დროის ფუნქცია ავზში, რომლიდანაც ხდება აირის ამოტუმბვა. ავზის მოცულობა არის V, საწისი წნევა არის p0. იგულისხმება, რომ პროცესი არის იზოთერმული და ამოტუმბვის სიჩქარე C არ არის წნევაზე დამოკიდებული. (იროდოვი 2.8)
ამოცანა 14.8
ხდება V მოცულობის ავზის ამოტუმბვა ტუმბოთი, რომლის ამოტუმბვის სიჩქარე არის C. რა დროში დაიკლებს ავზში წნევა η-ჯერ? (იროდოვი 2.9)
ამოცანა 14.9
იპოვეთ იდეალური აირის მაქსიმალურად შესაძლო ტემპერატურა შემდეგი პროცესებისთვის
(ა) \(p=p_{0}-\alpha V^{2}=p_{0}-\alpha \left ( \frac{RT}{p} \right )^{2}\)
(ბ) \(p=p_{0}e^{-\beta V}\)
სადაც \(p_{0}\), \(\alpha\) და \(\beta\) დადებითი სიდიდეებია, V კი - აირის მოცულობა (იროდოვი 2.11)
ამოცანა 14.10
განსაზღვრეთ იდეალური აირის შესაძლო უმცირესი წნევა \(T=T_{0}+\alpha V^{2}\) კანონით მიმდინარე პროცესში, სადაც To და \(\alpha\) დადებითი მუდმივებია, V კი - აირის ერთი მოლის მოცულობა. (იროდოვი 2.12)
ამოცანა 14.11
გამოთვალეთ სიმაღლეთა სხვაობა, რომლებზეც ჰაერის სიმკვრივე 0oC ტემპერატურაზე განსხვავდება:
ა) e-ჯერ, ბ) \(\eta =\)1%-ით, თუ ჰაერის ტემპერატურა, მოლური მასა, და სიმძიმის ძალის აჩქარება არ არის დამოკიდებული სიმაღლეზე. (იროდოვი 2.16)
ვთქვათ, დედამიწის ზედაპირთან ჰაერი ნორმალურ პირობებშია. თუ დავუშვებთ, რომ ჰაერის ტემპერატურა და მოლური მასა არ არიან დამოკიდებული სიმაღლეზე, იპოვეთ მისი წნევა დედამიწის ზედაპირიდან 5,0 კმ სიმაღლეზე და 5,0 კმ სიღრმის შახტაში. (იროდოვი 2.15)
ამოცანა 14.13
გამოთვალეთ γ=Cp/Cv სიდიდე იდეალური აირების ნარევისთვის, რომლებიც შედგება v1=2.0მოლი ჟანგბადისგან და v2=3.0მოლი ნახშირორჟანგისგან. (იროდოვი 2.33)
ამოცანა 14.14
T0=290 K ტემპერატურის მქონე ჟანგბადის ერთი მოლი ადიაბატურად შეკუმშეს ისე, რომ წნევა η=10,0-ჯერ გაიზარდა. იპოვეთ:
ა) აირის ტემპერატურა შეკუმშვის შემდეგ;
ბ) აირის შეკუმშვაზე შესრულებული მუშაობა. (იროდოვი 2.39)
ამოცანა 14.15
γ ადიაბატის მაჩვენებლიანი ერთი მოლი იდეალური აირის მოცულობა იცვლება V=α/T კანონით, სადაც α მუდმივაა. იპოვეთ აირის მიერ მიღებული სითბოს რაოდენობა ამ პროცესში, თუ ტემპერატურის ნაზრდი არის ∆T. (იროდოვი 2.43)
თუ ორი ურთიერშემხები ფენა მოძრაობს განსხვავებული სიჩქარეებით, შეიძლება მოხდეს აირის ფენების სიჩქარეების გათანაბრება. საშუალოდ ასეთი ფენების მოლეკულების იმპულსები განსხვავებულია - უფრო სწრაფი ფენების მოლეკულებს აქვთ უფრო მეტი იმპულსის მნიშვნელობები. სწრაფი შრიდან მოლეუკულების უფრო ნელ შრეში გადასვლას თან ახლავს მოწესრიგებული მოძრაობის იმპულსის გადატანა. საპირისპირო ეფექტს იძლევა უფრო ნელი შრიდან მოლეკულების გადასვლა უფრო სწრაფ შრეში. ჯამური ეფექტი არის სიჩქარეების გათანაბრება. ამ ეფექტს ეწოდება შინაგანი ხახუნი. ამასთან, ნიუტონის მიერ ჩამოყალიბებული კანონი ამბობს: სიბლანტის ძალა F პროპორციულია 
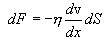 |
(13.3) |
η - შინაგანი ხახუნის კოეფიციენტია (დინამიური სიბლანტე). მოლეკულურ-კინეტიკური თეორიის მიხედვით