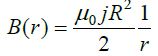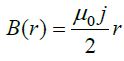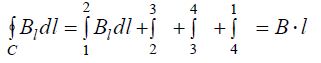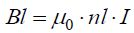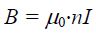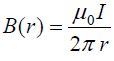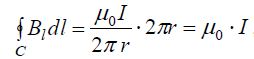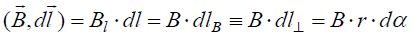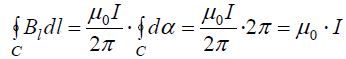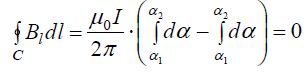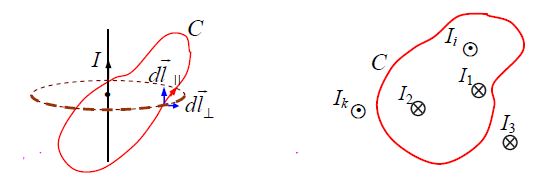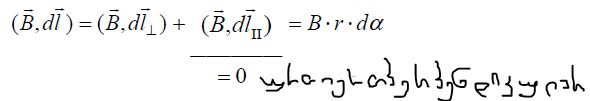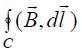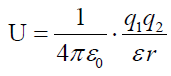როგორც უკვე ავღნიშნეთ ცირკულაციის თეორემის გამოყენება გამართლებულია ბრტყელი ცილინდრული და სფერული სიმეტრიების ამოცანების გადასაჭრელად. ამ შემთხვევებში კონტურის ფორმა (23.1) განტოლებაში შეიძლება დავიყვანოთ 
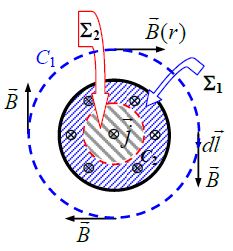
მაგალითი 1. გძელ სწორხაზოვან R რადიუსის მქონე გამტარში გადის დენი. დენის სიმკვრივე თანაბრად არის განაწილებული განიკვეთში და ტოლია j-ს. ვიპოვნოთ მაგნიტური ინდუქციის ვექტორის რადიუსზე დამოკიდებულება გამტარის შიგნით და მის გარეთ.
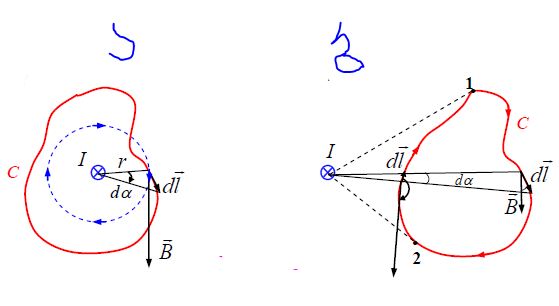
ძალიან გრძელი (მკარცრად რომ ვთქვათ, უსასრულო სიგრძის) გამტარისთვის შეიძლება ამოცანის ცილინდრულ სიმეტრიაზე ვისაუბროთ, ანუ გამტარისადმი პერპენდიკულარულ ნებისმიერ სიბრტყეზე მაგნიტური ველის ძალწირები არის წრეწირები, რომელთა ცენტრები ემთხვევა გამტარს. 
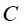
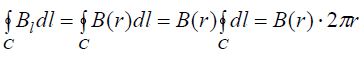
უნდა ვიგულისხმოთ, რომ ინდუქციის 
ფორმით მაგნიტური ველის ცირკულაციის გამოსახულება ორივე კონტურისთვის ერთნაირია - 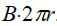
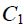
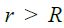
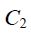
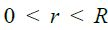
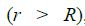
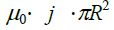
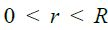
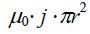
ხოლო გამტარს შიგნით კი:
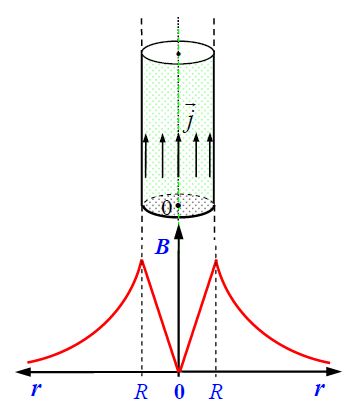
ნახაზზე გამოსახულია ღერძიდან რადიალური მიმართულებით დენიანი გამტარის მაგნიტური ველის ცვლილება. ცხადია ველის მიმართულება ნებისმიერ წერტილში განისაზღვრება მარჯვენა ბურღის წესით.
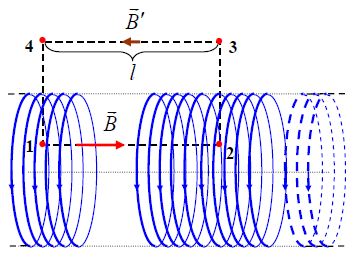
მაგალითი 2. ვიპოვნოთ სოლენოიდის მაგნიტური ინდუქცია
ამასტან კონტურის ერთ-ერთი გვერდი 1-2 მოთავსებულია სოლენოიდის შიგნით, ხოლო მეორე 3-4 მის გარეთ. 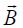
ეს ასეა, რადგან მეორე და მეოთხე წევრები ნულებია რადგან მათ ინტეგრალქვეშა ვექტორები ურთიერთპერპენდიკულარულებია და სკალარული ნამრავლები იძლევა ნულს. კონტურის 3-4 მონაკვეთი შეგვიძლოია ავიღოთ სოლენოიდიდან რაგინდ შორს იქ სადაც მაგნიტური ინდუქცია ნულია (ბიო-სავარ-ლაპლასის კანონი) და ამიტომ მეოთხე წევრიც არის ნული. ამიტომ ცირკულაციის გამოსახულება სრულად განისაზღვრება სოლენოიდის შიგნით მაგნიტური ინდუქციით და იგი ტოლი იქნება:
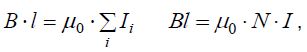
სადაც 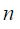
3-4 ბნის განლაგებაზე სოლენოიდის მაგნიტური ინდუქციის დამოუკიდებლობა იმაზე მეტყველებს, რომ სოლენოიდის გარეთ მაგნიტური ველი ძალიან სუსტია, ანუ მთელი მაგნიტური ველი მოქცეულია სოლენოიდის შიგნით. ამ მხრივ სოლენოიდი მაგნიტიზმში თამაშობს ელექტრობაში კონდენსატორის ანალოგიურ როლს.
გაუსის თეორემის დამტკიცების მსგავსად ნაბიჯ-ნაბიჯ ვაწარმოოთ თეორემის მტკიცება უმარტივესიდან რთულისკენ.
ა) განვიხილოთ ჯერ უმარტივესი შემთხვევა – მუდმივი დენი უსასრულოდ გრძელ წვრილ სწორხაზოვან სადენში.
კონტური 
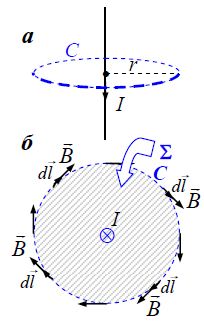
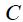
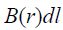
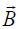
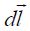
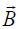
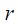
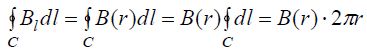
ბიო-სავარ-ლაპლასის კანონისა და სუპერპოზიციის პრინციპის გამოყენების შედეგად უკვე ვიცით, რომ უსასრულოდ გრძელი სწორგაზოვანი დენიანი სადენისთვის
ამის ჩასმით (*) გამოსახულებაში მივიღებთ:
რაც სწორედ ემთხვევა ჩვენი თეორემის მტკიცებულებას.
ბ) ოდნავ გავართულოთ მდგომარეობა - ვთქვგათ 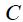
ჩავწეროთ გეომეტრიული მოსაზრებებიდან გამომდინარე ცხადი გამოსახულებები:
ჩავსვათ მასში მაგნიტური ინდუქციის გამოსახულება უსასრულოდ გრძელი სწორხაზოვანი დენიანი გამტარისთვის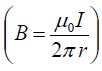
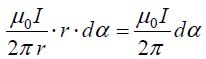
ახლა ამოცანა გამარტივდა, რადგან ერთადერთი ცვლადი დარჩა 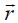
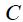
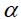
რაც ისევ ემთხვევა თეორემის მტკიცებულებას.
გ) ვთქვათ ახლა გამტარი გადის კონტურს გარეთ (ნახ. ბ).
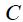
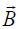
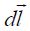
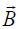
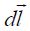
ეს ნიშნავს, რომ კონტურს გარეთ მოქცეულ დენებს ცირკულაციაში წვლილ არ შეაქვთ.
დ) დაგვრჩა განვაზოგადოდ შედეგები, როცა კონტური არ არის ბრტყელი (ადვილი მისახვედრია, რომ შდეგი ამავდროულად ზოგადი იქნება, როცა გამტარი არ არის სწორხაზოვანი) და თვით გამტარები რამდენიმეა (ბევრია).
არაბრტყელი კონტურის ნებისმიერი მცირე უბანი შეგვიძლია წარმოვადგინოთ გამტარის პერპენდიკულარული 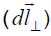
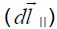
შემდგომ კი ბ) და გ) პუნქტების გამოყენება მიგვიყვანს უკვე ცნობილ შედეგებამდე 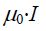
ე) დაგვრჩა განვაზოგაგოთ შედეგები ნებისმიერი რაოდენობის დენისთვის.
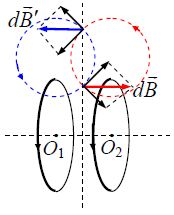
ამ ნაწილის სამართლიანობა პირდაპირ ჩანს ნახაზიდან და მაგნიტური ინდუქციის ვექტორის სუპერპოზიციის პრინციპიდან. იგივე ითქმის კონტურში დენის ნებისმიერი განაწილებისთვის. ამ შემთხვევაში დენების დისკრეტული მნიშვნელობების ჯამი იცვლება უწყვეტი ინტეგრებით 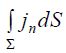
თეორემა დამტკიცებულია!
მაგნიტური ველის ძალური მახასიათებლის, 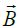
ელექტროსტატიკის მსგავსად მაგნეტოსტატიკაში (ანუ უძრავი მუდმივდენიანი გამტარების შემთხვევაში) ვაყალიბებთ 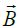
უწინარეს ყოვლისა შემოვიტანოთ თვით ვექტორული ველის ცირკულაციის ცნება მაგნიტოსტატიკური ველის მაგალითზე.. .
(განსაზღვრება) ვექტორის (მაგალითად 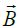
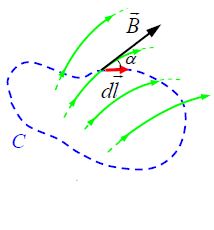
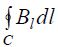
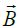
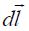
ახლა კი ჩამოვაყალიბოთ თეორემა.
მაგნიტოსტატიკური ველის ინდუქციის 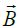
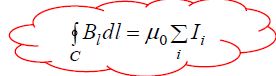
ერთეულთა SI სისტემაში პროპორციულობის კოეფიციენტი 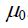
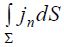
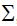
ელექტრული მუხტი
ელექტრული მუხტი არის ნაწილაკებისა და სხეულების ელექტრული და მაგნიტური ურთიერთქმედების უნარის საზომი.
ძირიტადი თვისებები:
1. არსებობს „დადებითი“ და „უარყოფითი“ მუხტები. მათ შორის არ არსებობს რაიმე ფუნდამენტური განსხვავება - ანუ სამყაროში არაფერი შეიცვლებოდა თუ შევცვლიდით „-“ ნიშანს „+“ ნიშნით.
2. ელექტრული მუხტი არის ზოგი ნაწილაკის განუყოფელი თვისება! ელექტრული მუხტის მინიმური წილი (|e| \(\cong\)1,6×10-19 კლ) ერთნაირია უარყოფითი და დადებითი ელექტრობისთვის - ამ ტოლობის ფარდობითი სიზუსტე არ არის უარესი 10-20-ზე! მაკროსკოპული სხეულების მუხტი q არის ადიტიური სიდიდე და იცვლება დისკრეტულად, ანუ ყოველთვის სრულდება q = ±N·|e|.
3. ელექტრული მუხტი ემორჩილება კიდევ ერთ ფუნდამენტურ კანონს - ელექტრული მუხტის შენახვის კანონს:
ელექტრულად იზოლირებულ სისტემაში ელექტრული მუხტების ალგებრული ჯამი არ იცვლება დროის განმავლობაში (\(\sum q_{i}=const\)).
ელექტრულად იზოლირებული ეწოდება სისტემას რომელსაც არ ტოვებენ და რომელშიც გარედან არ აღწევენ დამუხტული სხეულები ან ნაწილაკები.
4. ელექტრული მუხტი ათვლის სისტემის არჩევის მიმართ არის ინვარიანტული (ანუ არ არის მასზე დამოკიდებული). ამას გარდა, ის არ არის დამუხტული ნაწილაკის მოძრაობის მდგომარეობაზე.
კულონის კანონი
ორ უძრავ წერტილოვან მუხტს შორის ურთიერთქმედების ძალა ვაკუუმში პირდაპირპროპორციულია ამ მუხტების მოდულების ნამრავლის და უკუპროპორციულია მათ შორის მანძილის კვადრატის. ეს ძალა არის მიზიდვის თუ მუხტები საპირისპირო ნიშნებისაა და - განზიდვის თუ ისინი ერთნიშნაა. ძალა მიმართულია მუხტების შემაერთებელი წრფის გასწვრივ.
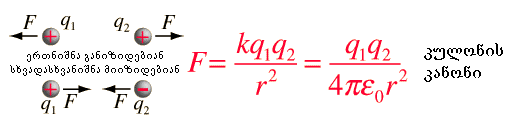
ε0 არის დიელექტრიკული შეღწევადობა.
სუპერპოზიციის პრინციპი
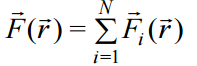
ელექტრული ველის დაძაბულობა
ელექტრული ველის დაძაბულობა ეწოდება ველის მოცემულ წერტილში მოთავსებულ საცდელ (წერტილოვან) მუხტზე მოქმედი ძალის ფარდობას ამ საცდელი მუხტის სიდიდესთან.
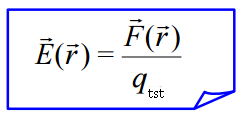 (15.3)
(15.3)
აქ 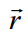 არის ათვლის მოცემულ სისტემაში წერტილის მდებარეობის მახასიათებელი რადიუს-ვექტორი.
არის ათვლის მოცემულ სისტემაში წერტილის მდებარეობის მახასიათებელი რადიუს-ვექტორი.
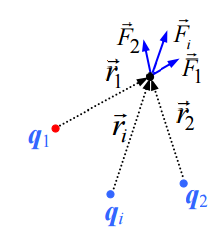
სუპერპოზიციის პრინციპი
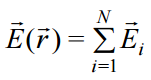
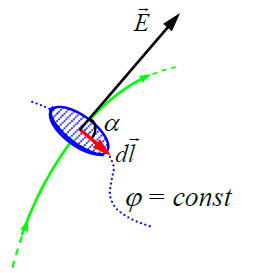
წერტილოვანი მუხტის ელექტრული ველი
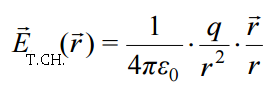
ელექტრული ველის დაძაბულობის წირები
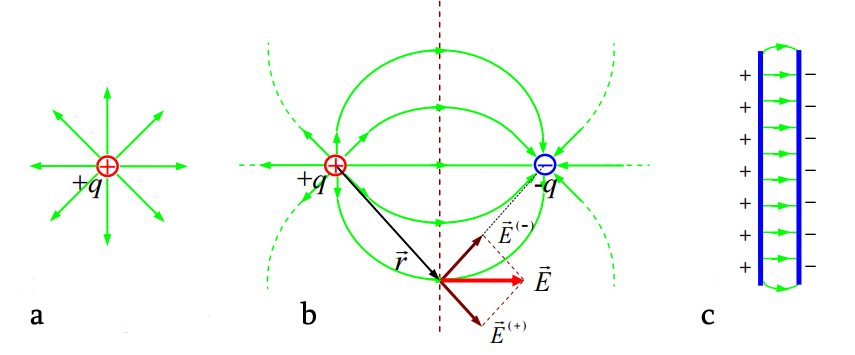 წირებს, რომლის ყოველ წერტილში მხებები ემთხვევა ელექტრული ველის დაძაბულობის ვექტორის მიმართულებას მოცემულ წერტილში, ეწოდებათ ელექტრული ველის დაძაბულობის წირები (ძალწირები).
წირებს, რომლის ყოველ წერტილში მხებები ემთხვევა ელექტრული ველის დაძაბულობის ვექტორის მიმართულებას მოცემულ წერტილში, ეწოდებათ ელექტრული ველის დაძაბულობის წირები (ძალწირები).
დაძაბულობის ვექტორის ნაკადი
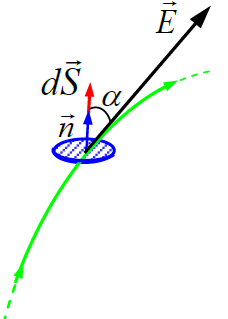
dS ელემენტურ ზედაპირში  ვექტორის ელემენტური ნაკადი dФ ეწოდება სიდიდეს:
ვექტორის ელემენტური ნაკადი dФ ეწოდება სიდიდეს:
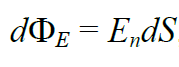
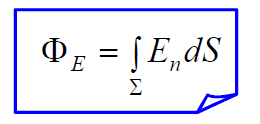
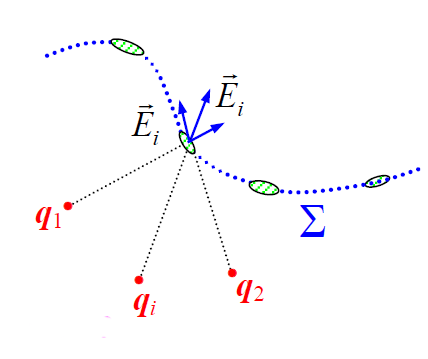
მუხტების სისტემის ველის დაძაბულობის ნაკადი ცალკეული მუხტების ნაკადების ალგებრული ჯამის ტოლია:
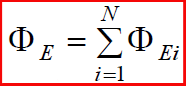
~
გაუსის თეორემა
♦ ვაკუუმში ნებისმიერ ზედაპირში ელექტროსტატიკური ველის დაძაბულობის ვექტორის ნაკადი ამ ზედაპირის შიგნით მოთავსებული მუხტების ჯამური მუხტის პროპორციულია.
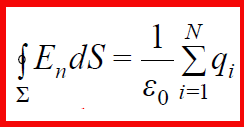
პოტენციალთა სხვაობა
(განსაზღვრება) 1 და 2 წერტილებს შორის ელექტროსტატიკური ველის პოტენციალთა სხვაობა ეწოდება ველის მიერ ამ წერტილებს შორის საცდელი მუხტის გადაადგილებაზე შესრულებული მუშაობის ფარდობას ამ საცდელი მუხტის სიდიდესთან.
\(\varphi _{1}-\varphi _{2}=\frac{A_{12}^{filed}}{q_{tst}}\)
პოტენციალი
მუშაობა, შეფარდებული მოცემული Р(x,y,z) წერტილიდან Р0 ნორმირების წერტილში გადასატანი საცდელი მუხტის სიდიდესთან.
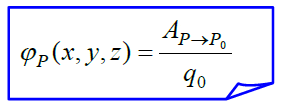
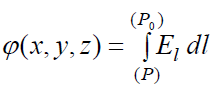
წერტილოვანი მუხტის ველის პოტენციალი
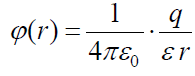
ელექტრულ ველში პოტენციური ენერგია
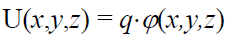
ელექტრულ ველში ორი წერტილოვანი მუხტის ურთიერთქმედების ენერგია
ექვიპოტენციური ზედაპირები
მუდმივი პოტენციალის მქონე ზედაპირები.
დაძაბულობის ძალწირები კვეთენ ექვიპოტენციურ ზედაპირებს მართი კუთხით!
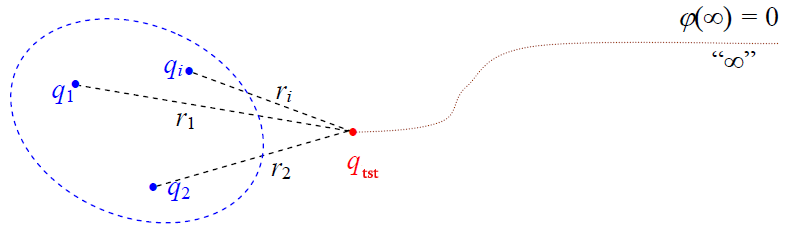
წერტილოვანი მუხტების ველის პოტენციალი
უხტების სისტემის ველის პოტენციალისთვის სამართლიანია სუპერპოზიციის პრინციპი: ის ცალკეული მუხტის მიერ მოცემულ წერტილში შექმნილი პოტენციალის ალგებრული ჯამის ტოლია:
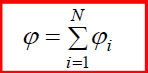
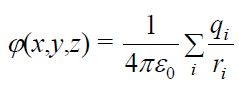
ელექტრული ველის დაძაბულობის კავშირი პოტენციალთა სხვაობასთან