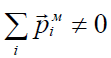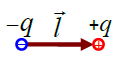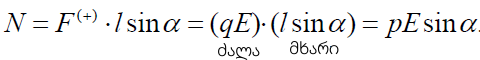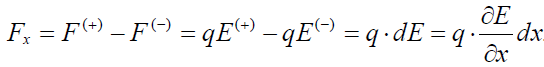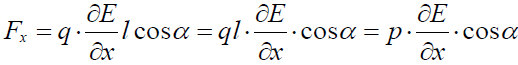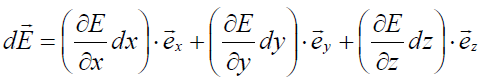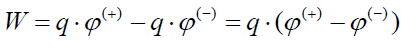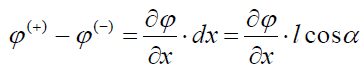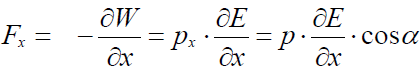მომავალში განვიხილავთ მხოლოდ აირად და თხევად (ან მყარ მაგრამ ამორფულ) არაგამტარ გარემოებს, ანუ ერთგვაროვან და იზოტროპულ დიელექტრიკებს. ასეთი ნივთიერებები შეიძლება შედგებოდეს, როგორც პოლარული, ისე არაპოლარული მოლეკულებისგან. სხვადასხვა დიელექტრიკებში პოლარიზაციის მექანიზმებიც განსხვავებულია.
1. ორიენტაციული (დიპოლური) პოლარიზაცია
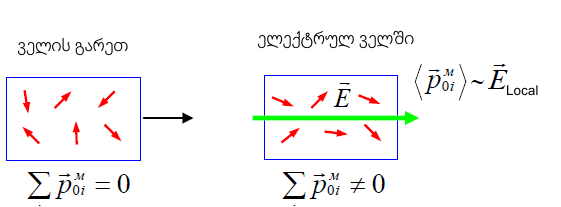
ასეთი მექანიზმი ახასიაბს, გარემოს, რომლის პოლარული მოლეკულებსაც აქვთ დიპოლური მომენტი 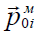
თითოეული მაკროსკოპული უბნის საშუალო დიპოლური მომენტი ხდება ნულკისგან განსხვავებული. ცდა აჩვენებს, რომ ის პროპორციულია მოლეკულებზე მოქმედი ელექტრული ველის დაძაბულობისა.
შენიშვნა
გამოთვლები სტატისტიკური ფიზიკის კანონების გამოყენებით იძლევა მისი მნიშვნელობის ზუსტ რაოდენობრივ დამოკიდეებულებასაც:
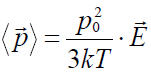
ასეთი შედეგი თვისობრივად გამოთვლების გარეშეც გასაგებია. რაც მეტია ველის დაძაბულობა, მით მეტია, ცხადია, მისი მაორიენტებელი ზემოქმედება – ანუ 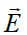
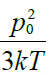
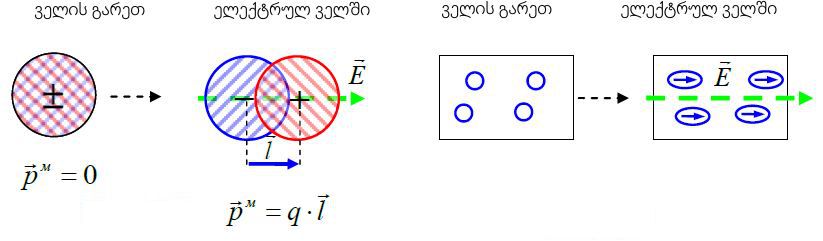
2. ელექტრონული პოლარიზაცია (წანაცვლების პოლარიზაცია)
ნივთიერება შეიძლება შედგებოდეს არაპოლარული მოლეკულებისგან, მაგალითად Ar, H2, N2, O2, CCl4, … . გარე ველის არ არსებობის შემთხვევაში ასეთ მოლეკულებს არ გააჩნიათ დიპოლური მომენტი. ის წარმოიქმნება მხოლოდ ველის ზემოქმედებით ელექტრონების სიმკვრივის წანაცვლებით მოლეკულის შიგნით ველის გასწვრივ. ჩვეულებრივ ასეთი წანაცვლების სიდიდე არც თუ ისე ძლიერ ველებში (<109ვ/მ) არ აღემატება ერთ ნანომეტრს და არის ველის დაძაბულობის პროპორციული (l ~ E – ჰუკის კანონში ზამბარის წაგრძელების მსგავსად). აქედან არის სწორედ მოცემული ტიპის პოლარიზაციის კიდევ ერთი სახელწოდება – "დრეკადი" პოლარიზაცია. აღძრული დიპოლური მომენტები მცირეა, მაგრამ სამაგიეროდ მკაცრად პარალელურია გარე ველის დაძაბულობისა 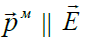
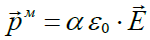
კოეფიციენტ \(\alpha\)-ს ამ თანაფარდობაში უწოდებენ მოლეკულების პოლარიზებულობას,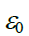
მოლეკულის პოლარიზებულობა არ არის დამოკიდებული ველის დაძაბულობაზე და არ არის დამოკიდებული ტემპერატურაზე!
შენიშვნა
არსებობს პოლარიზაციის კიდევ ერთი ტიპი – იონური მესერი. როგორც სახელწოდებიდანაც ჩანს, ასეთი პოლარიზაცია ახასიათებს კრისტალებს - მყარ სხეულებს (Cl, CsCl, …). მათთვის შესაძლებელია ელექტრული თვისებების ანიზოტროპია და საკითხის განხილვა რთულდება. ჩვენ კი შემოვიფარგლებით მხოლოდ თხევადი და აირადი იზოტროპული დიელექტრიკების განხილვით.
უკვე ვიცით რაღაც ელექტრულ ველზე დამუხტულ სხეულებს შორის რაიმე გარემოს არ არსებობის შემთხვევაში (ვაკუუმი). თითქმის არაფერი იცვლება გაუხშოებული აირის – მაგალითად, ჰაერის არსებობის შემთხვევაში. გარდა ამისა, გავარკვიეთ, რომ გამტარებში და გამტარი გარსის შიგნით ელექტროსტატიკური ველი გარედან არ აღწევს 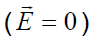
გავიხსენოთ, რომ დიელექტრიკები ეწოდებათ დენის არაგამტარ სხეულებს ("იზოლატორები"), რადგან მათში არ არის თავისუფალი მუხტის გადამტანი ნაწილაკები. თუმცა მათში, რა თქმა უნდა არიან დამუხტული ნაწილაკები, რომლებიც შედიან ატომებისა და მოლეკულების შემადგენლობაში – ე.წ. "ბმული მუხტები". გარე ველის მოქმედებით ასეთი მუხტები შეიძლება წანაცვლდნენ არაუმეტეს 10-9 მ (ანუ ერთი ნანომეტრი) მანძილისა. ამბობენ, რომ შედეგად დიელექტრიკი პოლარიზდება – მისი ჯამური დიპოლური მომენტი ხდება ნულისგან განსხვავებული:
აქ 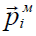
დიელექტრიკების შესწავლამდე მოკლედ შევეხოთ დიპოლების საკითხს, რაც განმსაზღვრელ როლს თამაშობს დიელექტრიკებში ელექტრული ველის ანალიზისას.
(განსაზღვრება) ელექტრული დიპოლი ეწოდება სისტემას, ორი ერთნაირი მოდულისა და საპირისპირო ნიშნის მქონე წერტილოვანი მუხტისგან q , რომლებიც ერთმანეთისგან დაშორებულია l მანძილით
დიპოლის ძირითადი მახასიათებელი არის მისი დიპოლური მომენტი:
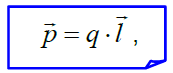
სადაც ვექტორს 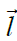
დიელექტრიკებში ელექტრული ველების თვისებების შესწავლამდე, გავარკვიოთ როგორ იქცევა დიპოლი გარეშე ელექტრულ ველში.
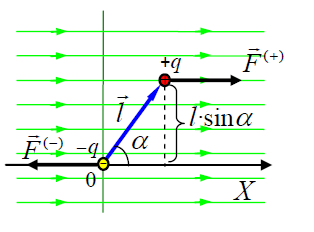
ერთგვაროვანი ველი. დავიწყოთ ერთგვაროვანი ველის შემთხვევიდაან
რადგან ასეთი ველის დაძაბულობა ერთნაირია სივრცის ყოველ წერტილში, ძალები 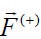
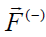
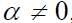
შეიძლება დავწეროთ ძალის მომენტის ვექტორიც:
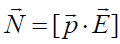
ამდენად, ჩვენ ვხედავთ, რომ ერთგვაროვანი ელექტრული ველი დიპოლზე ახდენს მაორიენტირებელ ქმედებას და ცდილობს მოაბრუნოს იგი ისე, რომ 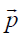
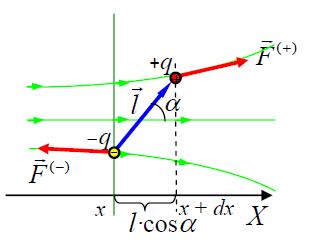
არაერთქვაროვანი ველი. არაერთგვაროვან ველში მაბრუნებელი მომენტის გარდა დიპოლზე მოქმედი ძალაც არ არის ნული. ამ ძალის მოსაძებნად ჩავთვალოთ ჯერ, რომ ველი იცვლება მხოლოდ ერთი მიმართულებით. ამ მიმართულებით მოვმართოთ ОХ კოორდინატთა ღერძი. დიპოლის მუხტებზე მოქმედი ძალები შევკრიბოთ:
აქ 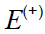
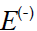
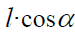
Fx მდგენელის ნიშანი განისაზღვრება, დაძაბულობის ვექტორის კოორდინატით წარმოებულით და დიპოლის ველისადმი ორიენტაციით (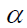
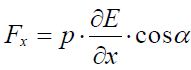
ვთქვათ კუთხე 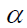
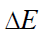
ხოლო დიპოლზე მოქმედი ძალა ზოგადად ჩაიწერება ასე:
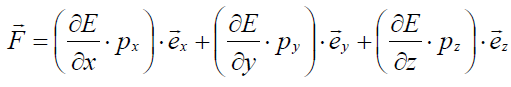
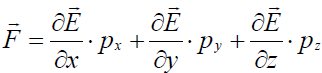
თუმცა მისი სახე მნიშვნელოვნად გართულდა, ზოგადი დასკვნა რჩება იგივე: დიპოლები ორიენტდებიან ძალწირების გასწვრივ და მიიზიდებიან მეტი დაძაბულობის ველის უბნისკენ.
სწორედ ასე იქცევა თხევადი პარამაგნიტური დიელექტრიკი, მაგალითად, ნავთი – ის შეიწოვება კონდენსატორის ფირფიტებს შორის.
დიპოლის ენერგია ელექტრულ ველში
როგორია დიპოლის ელექტრულ ველთან ურთიერთქმედების ენერგია? ამ ენერგიის გამოსათვლელად უმჯობესია გამოვიყენოთ წერტილოვანი მუხტების ელექტრულ ველთან ურთიერთქმედების ენერგია:
სადაც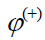
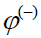
გავითვალისწინოთ ახლა დაძაბულობასა და პოტენციალს შორის კავშირი:
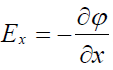
მაშინ დიპოლის ენერგია შეიძლება ამ სახით:
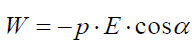
თუმცა ჩვენ ჩავთვალეთ, რომ ველი იცვლებოდა მხოლოდ ერთი მიმართულებით (ОХ), მიღებული შედეგი სამართლიანია ნებისმიერი ელექტრული ველისთვის. ამ შემთხვევაში 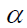
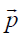
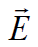 -ს შორის და გამოსახულება მოხერხებულია ჩაიწეროს ამ ვექტორების სკალარული ნამრავლის სახით:
-ს შორის და გამოსახულება მოხერხებულია ჩაიწეროს ამ ვექტორების სკალარული ნამრავლის სახით: 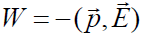
მიაქციეთ ყურადღება, რომ ჩვენს მიერ დიპოლზე არაერთგვაროვგანი ელექტრული ველის მხრიდან მოქმედი ძალისთვის ადრე მიღებული შედეგი (19.3), ახლა მარტივად შეიძლება იქნას მიღებული ჯერ კიდევ მექანიკიდან ცნობილი ძალასა და პოტენციურ ენერგიას შორის ზოგადი დამოკიდებულებიდან: 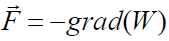
ენერგია, როგორც ვიცით არის სისტემის მიერ "მუშაობის შესრულების" მარაგი. ჩვენ შემთხვევაში ეს მარაგი წარმოიქმნება კონდენსატორის ფირფიტების დამუხტვისას მათი მუხტების განცალკევებაზე შესრულებული მუშაობის ხარჯზე. გამოვთვალოთ ეს მუშაობა. გარე ძალების მიერ კონდენსატორის ველში dq მუხტის გადასაადგილებლად შესრულებული ელემენტური მუშაობა ტოლია:

(აქ არ ღირს ყურადღების მიქცევა ნიშნების სისწორეზე. ნათელია, რომ გარე ძალების მუშაობა სრულდება ველის ძალების საწინააღმდეგოდ და ის იქნება დადებითი) სრული მუშაობა მიიღება ელემენტური მუშაობების აჯამვით ანუ ინტეგრირებით:

ჩვენ აქ დროებით გამოვიყენეთ აღნიშვნა Q კონდენსატორის მუხტის ზღვრული მნიშვნელობისთვის მათემატიკური კორექტულობისთვის, რათა განგვესხვავებინა ის "შუალედური" ("მიმდინარე") მნიშვნელობისგან რომელიც არის ინტერვალში  . სწორედ ეს მუშაობა განსაზღვრავს კონდენსატორში დამარაგებულ ენერგიას.
. სწორედ ეს მუშაობა განსაზღვრავს კონდენსატორში დამარაგებულ ენერგიას.
ისევე გამოვიყენოთ კავშირი კონდენსატორის მუხტსა და  პოტენციალთა სხვაობას შორის
პოტენციალთა სხვაობას შორის  . მაშინ შეიძლება ჩავწეროთ დამუხტული კონდენსატორის ენერგია ამ სახით:
. მაშინ შეიძლება ჩავწეროთ დამუხტული კონდენსატორის ენერგია ამ სახით:
 ანუ
ანუ  (18.11)
(18.11)
უკანასკნელ ტოლობაში მეტი კომპაქტურობისთვის შევცვალეთ  აღნიშვნა u-თი. ამ სიდიდეს ხშირად უწოდებენ "ძაბვას" კონდენსატორზე. თვით ენერგია კი ავღნიშნეთ ასე We. ეს არის სწორედ ელექტრული ველის ენერგია. ამის თქმის უფლებას გვაძლევს ის, რომ დღესდღეობით უკვე კარგად ვიცით, რომ თვით ველი ხშირ შემთხვევებში განცალკევდება მუხტისგან და ვრცელდება ელექტრომაგნიტური ტალღების სახით სივრცეში, გადააქვს რა შესაბამისად ენერგია და საერთოდ არ ახსოვს მისი წყარო მუხტი.
აღნიშვნა u-თი. ამ სიდიდეს ხშირად უწოდებენ "ძაბვას" კონდენსატორზე. თვით ენერგია კი ავღნიშნეთ ასე We. ეს არის სწორედ ელექტრული ველის ენერგია. ამის თქმის უფლებას გვაძლევს ის, რომ დღესდღეობით უკვე კარგად ვიცით, რომ თვით ველი ხშირ შემთხვევებში განცალკევდება მუხტისგან და ვრცელდება ელექტრომაგნიტური ტალღების სახით სივრცეში, გადააქვს რა შესაბამისად ენერგია და საერთოდ არ ახსოვს მისი წყარო მუხტი.
რადგან ენერგია ახასიათებს ველს, ამიტომ ვცადოთ მისი გამოსახვა თვით ამ ველის მახასიათებლით - რაც არის დაძაბულობა. თუმცა გამოსახულება (18,11) მიღებულია ნებისმიერი კონდენსატორისთვის, გამოვიყენოთ იგი ბრტყელი კონდენსატორის შიგნით. ვიცით, რომ იქ ველი ერთგვაროვანია, ანუ არსებობს უმარტივესი კავშირი პოტენციალთა სხვაობასა და დაძაბულობას შორის:  . ამას გარდა, ასეთი შემთხვევისთვის ვიცით ელექტროტევადობის გამოსახულება (18,10). მივიღებთ:
. ამას გარდა, ასეთი შემთხვევისთვის ვიცით ელექტროტევადობის გამოსახულება (18,10). მივიღებთ:

(18.12)
აქ V – კონდენსატორის ფირფიტებს შორის სივრცის მოცულობაა. ბრტყელი კონდენსატორის შიგნით ველის ერთგვაროვნება საშუალებას გვაძლევს, ახლა მიღებული შედეგის გამოყენებით, ადვილად გამოვსახოთ კიდევ ერთი საჭირო მახასიათებელი - ე.წ. ელექტრული ველის სივრცული სიმკვრივე. მოგვიანებით მოვიყვანთ ამ სიდიდის უფრო ზუსტ განსაზღვრებას. აქ კი, ერთგვაროვანი ველისთვის, ეს არის უბრალოდ ველის ენერგიის ფარდობა ფირფიტებს სივრცის მოცულობასთან, რომელშიც არის ეს ველი:
 (18.13)
(18.13)
მნიშვნელოვანია, რომ ენერგიის სიმკვრივე გამოვსახეთ ელექტრული ველის ძირითადი მახასიათებლით. ასევე მნიშვნელოვანია, რომ თუმცა (18,13) მივიღეთ ერთგვაროვანი ველისთვის, ის სამართლინი რჩება არაერთგვაროვანი ველისთვისაც. ენერგიის მოცულობითი სიმკვრივე - ველის ლოკალური მახასიათებელია, ანუ ის შეესაბამება სივრცის ნებისმიერ მცირე უბანს, სადაც ველის დაძაბულობა არის E.
დავაზუსტოთ ენერგიის მოცულობითი სიმკვრივის ცნება. ზოგად შემთხვევაში გამოვყოთ არაერთგვაროვანი ველის dV მცირე ელემენტი, რომლის მდებარეობა მოიცემა  რადიუსვექტორით ან {x,y,z} კოორდინატებით.
რადიუსვექტორით ან {x,y,z} კოორდინატებით.
(განსაზღვრება.) ენერგიის მოცულობით სიმკვრივე ეწოდება სიდიდეს


სადაც dWe სივრცის ამ მცირე ელემენტში მოქცეული ენერგიაა. თუ ცნობილია ველის დაძაბულობის კოორდინატზე დამოკიდებულება  , შეიძლება გამოითვალოს ამ ველის სრული ენერგია
, შეიძლება გამოითვალოს ამ ველის სრული ენერგია  სივრცის ამა თუ იმ სასრული ზომების უბანში:
სივრცის ამა თუ იმ სასრული ზომების უბანში:

(18.15)
ინტეგრირება ხდება მთელ  სივრცეზე, რომლისთვისაც გამოითვლება ველის ენერგია. აქ ისევ ვეჯახებით მოცულობითი ინტეგრალის აღების სირთულეს, რომელიც რიგ აქტუალურ (პრაქტიკაში მნიშვნელოვან) შემთხვევაში შეიძლება დაყვანილი იქნას ჩვეულებრივ განსაზღვრულ ინტეგრირებაზე.
სივრცეზე, რომლისთვისაც გამოითვლება ველის ენერგია. აქ ისევ ვეჯახებით მოცულობითი ინტეგრალის აღების სირთულეს, რომელიც რიგ აქტუალურ (პრაქტიკაში მნიშვნელოვან) შემთხვევაში შეიძლება დაყვანილი იქნას ჩვეულებრივ განსაზღვრულ ინტეგრირებაზე.
აღვნიშნოთ, რომ გამოსახულება (18.15) ჩაწერილია ისეთი დიელექტრიკული გარემოსთვის, რომელსაც აქვს ერრთგვაროვანი ელექტრიკული მახასიათებლები, ანუ  . შემთხვევისთვის. წინააღმდეგ შემთხვევაში დიელექტრიკული შეღწევადობა რჩება ინტეგრალს შიგნით. აღვნიშნოთ, ასევე, რომ ისინი რჩება სამართლიანი დროში ცვლადი ველისთვისაც ანუ მაგალითად ელექტრომაგნიტური ტალღებისთვის.
. შემთხვევისთვის. წინააღმდეგ შემთხვევაში დიელექტრიკული შეღწევადობა რჩება ინტეგრალს შიგნით. აღვნიშნოთ, ასევე, რომ ისინი რჩება სამართლიანი დროში ცვლადი ველისთვისაც ანუ მაგალითად ელექტრომაგნიტური ტალღებისთვის.