ელექტრული ველის დაძაბულობა არის ვექტორული სიდიდე. გარკვეულ შემთხვევებში უფრო მოხერხებულია ველის სკალარული მახასიათებლების - პოტენციალთა სხვაობისა და პოტენციალის გამოყენება. მათი განსაზღვრებისთვის დავეყრდნობით მუხტზე ელექტრულ ველში მოქმედი ძალის კონსერვატულობის თვისებას. კონსერვატულობის თვისება გამომდინარეობს კულონის ძალის ცენტრულობიდან. კლასიკური მექანიკის განმარტებით ცენტრული ეწოდება ძალას, რომლის სიდიდეც დამოკიდებულია მხოლოდ ურთიერთქმედ სხეულებს შორის მანძილზე და მიმართულია მათ ცენტრებს შორის შემაერთებელი წირის გასწვრივ. გავიხსენოთ ასევე, რომ კონსერვატული ეწოდება ძალებს, რომელთა შესრულებული მუშაობა არ არის დამოკიდებული მოძრაობის ტრაექტორიის ფორმაზე. ასეთი ძალების მიერ შესრულებული მუშაობა განისაზღვრება მხოლოდ სხეულის გადაადგილების საწყისი და საბოლოო კოორდინატებით.
ელექტრული ველების სუპერპოზიციის პრინციპიდან გამომდინარეობს, რომ საცდელი მუხტის გადაადგილებაზე შესრულებული მუშაობა უძრავი მუხტების მიერ შექმნილ ველში, არის ალგებრული ჯამი მუშაობებისა, რომელსაც ასრულებენ თითოეული შემადგენელი მუხტის მხრიდან საცდელ მუხტზე მოქმედი ძალები. ანუ ასეთი ძალების („კულონური ძალების“) ველი ასევე არის კონსერვატული.
ამდენად, წერტილოვანი მუხტის წერტილი 1-დან წერტილ 2-ში გადაადგილებაზე ველის მიერ შესრულებული მუშაობა A1-2 არის ამ ველის მახასიათებელი. მაგრამ ის დამოკიდებულია საცდელი მუხტის სიდიდეზეც. იმისათვის რათა დავახასიათოთ მხოლოდ ველი, უნდა გავყოთ ეს მუშაობა საცდელი მუხტის სიდიდეზე. რასაც მივიღებთ არის სწორედ „პოტენციალთა სხვაობა“.
(განსაზღვრება) 1 და 2 წერტილებს შორის ელექტროსტატიკური ველის პოტენციალთა სხვაობა ეწოდება ველის მიერ ამ წერტილებს შორის საცდელი მუხტის გადაადგილებაზე შესრულებული მუშაობის ფარდობას ამ საცდელი მუხტის სიდიდესთან.
\(\varphi _{1}-\varphi _{2}=\frac{A_{12}^{filed}}{q_{tst}}\) (17.1)
Si სისტემაში პოტენციალთა სხვაობის ერთეული არის ვოლტი (1ვოლტი=1ჯოული/კულონი). თუ ვისწავლით რამენაირად (თეორიულად ან ექსპერიმენტულად) უძრავი მუხტების სისტემის ველის 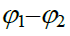 პოტენციალთა სხვაობის განსაზღვრას, ეს მოგვცემს საშუალებას ნებისმიერი წერტილოვანი q მუხტის ამ ველში გადაადგილებაზე ველის მიერ შესრულებული მუშაობა ვიპოვოთ ფორმულით:
პოტენციალთა სხვაობის განსაზღვრას, ეს მოგვცემს საშუალებას ნებისმიერი წერტილოვანი q მუხტის ამ ველში გადაადგილებაზე ველის მიერ შესრულებული მუშაობა ვიპოვოთ ფორმულით:
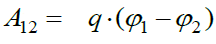 (17.2)
(17.2)
ამდენად, პოტენციალთა სხვაობა არის ელექტრული ველის ენერგეტიკული მახასიათებელი, რადგან უშუალო კავშირშია მუშაობის ცნებასთან.
მექანიკაში გვახსოვს პოტენციური ენერგიის ცნება და მუშაობის განმარტება, პრინციპით: ველის ძალების მუშაობა პოტენციური ენერგიის დანაკლისის ტოლია. ჩავწეროთ ფორმალურად ეს პრინციპი:
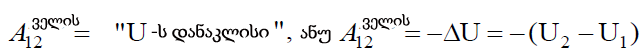 17.3)
17.3)
აქ U1 და U2 – პოტენციური ენერგიებია სისტემის «საწყის» («1») და «საბოლოო» («2») მდგომარეობებში, შესაბამისად. ჩვენი უძრავი მუხტების ელექტრული ველის შემთხვევაში - ეს არის წერტილოვანი q მუხტის ენერგია «1» (კოორდინატებით {x1,y1,z1})) მდგომარეობაში და მისი ენერგია «2» (კოორდინატებით{x2,y2,z2}) მდგომარეობაში. ანუ ამ ველში მუხტის პოტენციური ენერგია არის კოორდინატების სკალარული ფუნქცია U = U(x,y,z) (ან 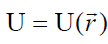 ). გამოსახულებების (17.2) და (17.3) შედარებით ვხედავთ, რომ მოხერხებულია ჩაითვალოს, რომ პოტენციალთა სხვაობა არის სხვაობა ველის წერტილთა კოორდინატების კიდევ ერთი სკალარული \(\varphi\left ( x,y,z \right )\)ფუნქციის . ის დაკავშირებულია U(x,y,z) პოტენციური ენერგიის ფუნქციასთან ამ მარტივი ტოლობით
). გამოსახულებების (17.2) და (17.3) შედარებით ვხედავთ, რომ მოხერხებულია ჩაითვალოს, რომ პოტენციალთა სხვაობა არის სხვაობა ველის წერტილთა კოორდინატების კიდევ ერთი სკალარული \(\varphi\left ( x,y,z \right )\)ფუნქციის . ის დაკავშირებულია U(x,y,z) პოტენციური ენერგიის ფუნქციასთან ამ მარტივი ტოლობით
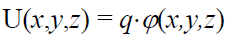 ანუ რადგან
ანუ რადგან
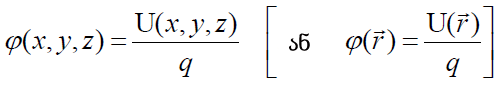 (17.4)
(17.4)
ამბობენ, რომ ის „რიცხობრივად ერთეულოვანი დადებითი მუხტის პოტენციური ენერგიის ტოლია“ ველის მოცემულ წერტილში. ამ ფუნქციას ეწოდება ელექტროსტატიკური ველის „პოტენციალი“ მოცემულ წერტილში.
მთავარი არის, თუ როგორ ვიპოვოთ ეს ფუნქცია 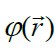 (და ე.ი.
(და ე.ი. 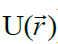 ) მუხტების კონკრეტული სისტემის ველისთვის, როგორი უნდა იყოს მოქმედებათა თანმიმდევრობა. უწინარეს ყოვლისა უნდა შევთანხმდეთ ნორმირების პირობებზე: უნდა აირჩეს წერტილი Р0, რომელშიც ველის პოტენციალს ჩავთვლით ნულად
) მუხტების კონკრეტული სისტემის ველისთვის, როგორი უნდა იყოს მოქმედებათა თანმიმდევრობა. უწინარეს ყოვლისა უნდა შევთანხმდეთ ნორმირების პირობებზე: უნდა აირჩეს წერტილი Р0, რომელშიც ველის პოტენციალს ჩავთვლით ნულად 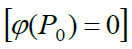 . ბევრ შემთხვევაში ასეთ წერტილს არჩევენ უსასრულოდ დაშორებულს, სადაც ველი არ არის
. ბევრ შემთხვევაში ასეთ წერტილს არჩევენ უსასრულოდ დაშორებულს, სადაც ველი არ არის 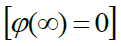
ამისათვის უნდა მოიძებნოს ველის „კუთრი“ მუშაობა - ანუ მუშაობა, შეფარდებული მოცემული Р(x,y,z) წერტილიდან Р0 ნორმირების წერტილში გადასატანი საცდელი მუხტის სიდიდესთან. ანალიზური სახით ეს პოტენციალის განსაზღვრება ასე შეიძლება ჩაიწეროს:
(განსაზღვრება)
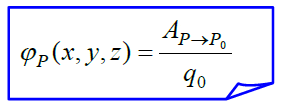 (17.5)
(17.5)
გამოვსახოთ პოტენციალთა სხვაობა და პოტენციალი ველის ძალური მახასიათებლებით. ამისთვის ვწერთ:
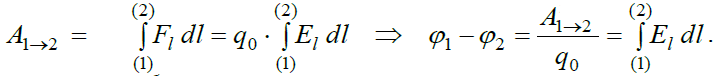
ამოვწეროთ უკანასკნელი ტოლობა:
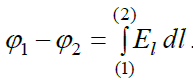 (17.6)
(17.6)
ეს გვაძლევს პოტენციალთა სხვაობის მოძებნის საშუალებას დაძაბულობის ცნობილი ფუნქციის მეშვეობით. ანალოგიურად პოტენციალისთვის:
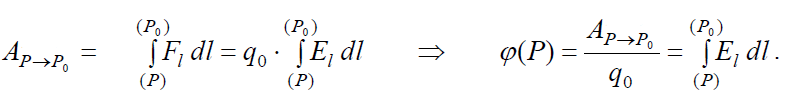
და საბოლოოდ ნებისმიერი (x,y,z) კოორდინატების მქონე Р წერტილის პოტენციალისთვის გვექნება:
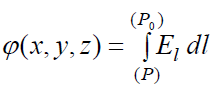 (17.7)
(17.7)
ადრე აღვნიშნეთ, მუხტის მოცემული განაწილების მიხედვით მისი ელექტრული ველის დაძაბულობის გათვლა სივრცეში შესაძლებელია სუპერპოზიციის პრინციპის გამოყენებით („პირველი მეთოდი“ – „უშუალოდ“) პრინციპულად ყოველთვის. მაგრამ გარდა ძალიან მარტივი შემთხვევებისა ასეთ გათვლებს ძალიან რთულ მათემატიკურ პროცედურებამდე მივყავართ. გაუსის თეორემა საშუალებას იძლევა მნიშვნელოვნად გავამარტივოთ ტექნიკური პრობლემები, ოღონდ თუ ადგილი აქვს გარკვეულ სიმეტრიას მუხტის სივრცულ განაწილებაში. ბრტყელი, ღერძული ან სფერული სიმეტრიის არსებობა არის პრინციპული მომენტი, ის საშუალებას იძლევა „აპრიორი“ გავაკეთოთ დასკვნა ველის სტრუქტურაზე, რის შემდეგაც შეიძლება შეირჩეს ვექტორის მოდულის ზედაპირის ნაწილის (ან მთელი ზედაპირის) ფართობზე ნამრავლზე. ამის შემდეგ რჩება მხოლოდ სწორად დავითვალოთ მუხტი შემოფარგლული იმ ზედაპირით, რომლშიც ვითვლით ნაკადს.
აქ ამის სადემონსტრაციოდ მოვიყვანთ ორ მაგალითს.
მაგალითი 1. ამოვხსნათ «ნიუტონის ამოცანა» – დავამტკიცოთ, რომ თანაბრად დამუხტული (დიელექტრული) სფეროს გარეთ ველი, არაფრით არ განსხვავდება წერტილოვანი მუხტის ველისგან მანძილებზე, რომელიც მეტია სფეროს R რადიუსზე
განვსაზღვროთ ასევე ველის დაძაბულობა სფეროს შიგნით (r ≤ R) ნებისმიერ წერტილში. ვთვლით, რომ სფეროს შიგნით q მუხტი განაწილებულია მუდმივი სივრცული სიმკვრივით \)\dpi{120} \rho\(, სფეროს მასალას აქვს დიელექტრული შეღწევადობა \)\dpi{120} \varepsilon\(.
დაწვრილებით წარმოვაჩინოთ ყველა ძირითადი ნაბიჯი, რაც საჭირო იქნება გაუსის თეორემით („მეორე მეთოდი“) ელექტრული ველის დაძაბულობის გამოსათვლელად.
•1. უნდა გაკეთდეს მუხტის სივრცეში განაწილების სქემატური ნახატი. მასზე მიეთითოს ამოცანის აუცილებელი პარამეტრები - ამ შემთხვევაში ბირთვის რადიუსი R, მუხტის განაწილების მახასიათებელი – მისი სიმკვრივე \)\dpi{120} \rho\(, სფეროს დიელექტრული შეღწევადობა \)\dpi{120} \varepsilon\(. უნდა შემოვიტანოთ შესაბამისი კოორდინატთა სისტემა (მუხტის განაწილების სიმეტრიის გათვალისწინებით), მიეთითოს ნახატზე საკოორდინატო ღერძები (როგორც წესი საკმარისია ხოლმე მხოლოდ ერთი) და ათვლის სათავე.
ჩვენს მაგალითში: მუხტი თანაბრად არის განაწილებული მთელ ბირთვში. მუხტის სიმკვრივე დამოკიდებულია მხოლოდ ცენტრიდან მანძილზე და არ არის დამოკიდებული სივრცეში მიმართულებაზე. ამასთან \)\dpi{120} \rho \left ( r \right )=const\( როცა r ≤ R და \)\dpi{120} \rho \left ( r \right )=0\( როცა r > R. ძნელი არის იმის მიხვედრა, რომ ამ მდგომარეობისთვის სათანადო იქნება სფერული კოორდინატთა სისტემა.

უფრო მეტიც, რადგან არ გვაქვს უპირატესი სივრცული მიმართულებები, ამიტომ არ დაგვჭირდება პოლარული კუთხეები და რუკაზე საკმარისია მხოლოდ კოორდინატთა სათავის (ცხადია ის უნდა შევუთავსოთ სფეროს ცენტრს და პოლარული ღერძის მითითება.
•2. მოვახდინოთ ველის სტრუქტურის ანალიზი. მუხტის განაწილების კონკრეტულ სიმეტრიაზე დაყრდნობით, გავაკეთოთ დასკვნა ელექტრული ველის დაძაბულობის ველის მიმართულებაზე ბირთვის შიგნით და მის გარეთ ნებისმიერ წერტილში. გავაკეთოთ დასკვნა რომელ კოორდინატებზე შეიძლება იყოს დამოკიდებული დაძაბულობის ვექტორის მოდული და რომლებზე არა. ნახატზე უნდა გაჩნდეს ვექტორები, რომელთაც ექნებათ საწყისი შესაბამის წერტილებში..
ჩვენს მაგალითში: ცალკეული წერტილოვანი მუხტის ელექტრული ველის თვისებები და სუპერპოზიციის პრინციპი გვაძლევს საშუალებას ვთქვათ, რომ არა მარტო მუხტის სივრცული განაწილებას, არამედ მის ელექტრული ველსაც აქვს რადიალური სიმეტრია. სივრცის ნებისმიერ წერტილში, როგორც ბირთვის შიგნით, ასევე მის გარეთ დაძაბულობის ვექტორი მკაცრად რადიუსის გასწვრივ არის მიმართული (ცენტრიდან, თუ მუხტი დადებითია და ცენტრისკენ, თუ მუხტი უარყოფითია). დაძაბულობის ვექტორი ალბათ დამოკიდებულია ცენტრიდან r მანძილზე, მაგრამ არავითარ შემთხვევაში მიმართულებაზე. ამიტო შემოვიღოთ აღნიშვნა \)\vec{E}(r)\(.
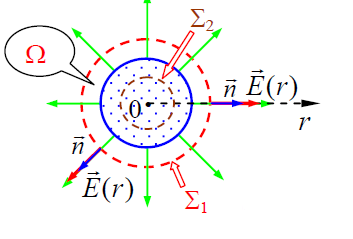
მივაქციოთ ყურადღება, რომ ფრჩხილებს შიგნით არის სწორედ დაშორების მოდული, ანუ მისი რიცხვითი მნიშვნელობა და არა ვექტორი! ნახაზზე ავარჩიოთ ორი ნებისმიერი წერტილი ბირთვის გარეთ და შიგნით და მათთვის მივუთითოთ დაძაბულობის ვექტორის მიმართულებები.
•3. სტრუქტურის ზევით ჩატარებული ანალიზის საფუძველზე ავარჩიოთ როგორც ადრე აღვნიშნეთ შერჩეული ზედაპირის ნაწილი დაძაბულობის ვექტორისადმი მართობული უნდა იყოს ნაწილი კი პარალელური. დაძაბულობის ვექტორის მოდული უნდა იყოს მუდმივი შერჩეული ზედაპირის ნაწილებისთვის. ნახაზზე უნდა გაჩნდეს ელემენტური ზედაპირებისადმი ნორმალი ვექტორები \(\vec{n}\) (ან \(d\vec{S}\), მათ ხომ თანხვედრი მიმართულებები აქვთ).
ჩვენს მაგალითში: ავარჩიოთ ნახაზზე ორი შეკრული ზედაპირი 2 – სფეროები, რომელთა ცენტრები ემთხვევა ბირთვის ცენტრს და რადიუსებით r > R და r < R შესაბამისად. ორი სხვადასხვა ზედაპირი დაგვჭირდა რათა ვიპოვოთ ნაკადი როგორც ბირთვის შიგნით ისე მის გარეთ. საყურადღებოა, რომ არჩეული ზედაპირი არ უნდა ემთხვეოდეს ბირთვის ზედაპირს და საერთოდაც არ უნდა ჰქონდეს გარკვეული რადიუსი, (მოცემულ შემთხვევაში R). ჩვენი ამოცანა ხომ შეადგენს ფუნქციის პოვნას და არა მისი კონკრეტული მნიშვნელობის პოვნას r-ის რაღაც გარკვეულ მნიშვნელობაზე.
•4. ახლა უნდა გამოვთვალოთ დაძაბულობის ვექტორის ნაკადი  ვექტორის მოდულისა და
ვექტორის მოდულისა და ჩვენს მაგალითში: რადგან ჩვენ შემთხვევაში და ერთნაირი მიმართულებისაა, ამიტომ
 ინტეგრალში სიდიდის ნაცვლად პირდაპირ დავწეროთ დაძაბულობის ვექტორის მოდული და იმის ხაზგასასმელად, რომ ეს სიდიდე არის მხოლოდ r მანძილის ფუნქცია, აღვნიშნოთ ეს სიდიდე ასე – E(r). r რადიუსის მქონე ზედაპირზე r-ის მნიშვნელობა რა თქმა უნდა მუდმივია და ამიტომ მუდმივია E(r) ფუნქციის მნიშვნელობაც. ის შეიძლება გავიტანოთ ინტეგრალს გარეთ:
ინტეგრალში სიდიდის ნაცვლად პირდაპირ დავწეროთ დაძაბულობის ვექტორის მოდული და იმის ხაზგასასმელად, რომ ეს სიდიდე არის მხოლოდ r მანძილის ფუნქცია, აღვნიშნოთ ეს სიდიდე ასე – E(r). r რადიუსის მქონე ზედაპირზე r-ის მნიშვნელობა რა თქმა უნდა მუდმივია და ამიტომ მუდმივია E(r) ფუნქციის მნიშვნელობაც. ის შეიძლება გავიტანოთ ინტეგრალს გარეთ:
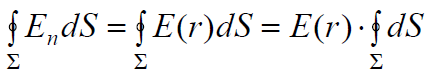
დარჩენილი ინტეგრალი წარმოადგენს 1 და \(\dpi{120} \Sigma\)2 – სფეროა. სფეროს ზედაპირის ფართობი არის 4πr2. საბოლოოდ
.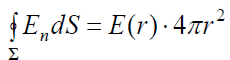
ამ შედეგის სახე ერთნაირია •5. ამის შემდეგ უნდა გამოვთვალოთ მუხტი, რომელიც შემოიფარგლა
ჩვენს მაგალითში: აქ კი შედეგის ჩანაწერი განსხვავებული იქნება
2 ზედაპირებისთვის. პირველ შემთხვევაში ზედაპირს შიგნით აღმოჩნდება ბირთვის მთელი მუხტი. ის ტოლია ბირთვის მუდმივი მოცულობითი სიმკვრივისა და ბირთვის მოცულობის ნამრავლის:

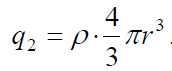
•6. და ბოლოს, დაგვრჩა ჩავწეროთ გაუსის თეორემის შესაბამისი ტოლობა. რადგან შერჩეული ზედაპირების რადიუსები ნებისმიერი იყო, ამიტომ შედეგი აღწერს სივრცის ნებისმიერ წერტილს და იქნება ზოგადი.
ჩვენს მაგალითში: ჩავწეროთ გაუსის თეორემის მოპასუხე ორი ტოლობა:

ა) my site.
აქედან ვასკვნით, რომ ბირთვის გარეთ ველის დაძაბულობა იცვლება კანონით 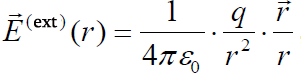 , როცა r > R (ველი ბირთვის გარეთ).
, როცა r > R (ველი ბირთვის გარეთ).
იმისათვის რათა ჩავრთოთ ჩაწერაში დაძაბულობის მიმართულებაც, ამიტომ უნდა გადავიდეთ ჩაწერის ვექტორულ ფორმაზე. ამასთან გავითვალისწინოთ, რომ 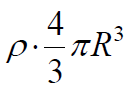 წარმოადგენს ბირთვის სრულ მუხტს. გვექნება:
წარმოადგენს ბირთვის სრულ მუხტს. გვექნება:
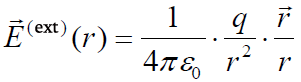 , როცა r > R (ველი ბირთვის გარეთ).
, როცა r > R (ველი ბირთვის გარეთ).
ამით ჩვენ დავამტკიცეთ, რომ თანაბრად დამუხტული ბირთვის ველის დაძაბულობა ბირთვის გარეთ ისეთივეა, როგორც წერტილოვანი მუხტისა r მანძილზე, რომლებიც მეტია ბირთვის R რადიუსზე. მას აქვს რადიალური მიმართულება და იცვლება მუხტის თავმოყრის ცენტრიდან დაშორების კვადრატის უკუპროპორციულად.
ბ) 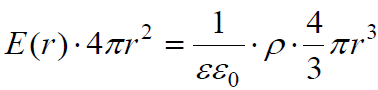
აქედან ვასკვნით, რომ ბირთვის შიგნით ველის დაძაბულობა იცვლება კანონით:
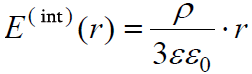 , როცა r ≤ R (ველი ბირთვის შიგნით).
, როცა r ≤ R (ველი ბირთვის შიგნით).
ან ვექტორული ფორმით:
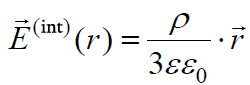 , როცა r ≤ R (ველი ბირთვის შიგნით).
, როცა r ≤ R (ველი ბირთვის შიგნით).
როგორც ვხედავთ ბირთვის შიგნით ველის დაძაბულობა მისი ცენტრიდან მანძილის პროპორციულია.
მაგალითი 2. განვსაზღვროთ R რადიუსის მქონე უსასრულოდ გრძელი ცილინდრული ძელაკის ელექტრული ველის დაძაბულობა ძელაკის ა) შიგნით და ბ) გარეთ. მუხტი თანაბრად იყოს განაწილებული ძელაკის შიგნით \(\dpi{120} \rho\) სივრცული სიმკვრივით; r – დაშორებაა ცილინდრის ღერძიდან, ძელაკის მასალის დიელექტრული შეღწევადობაა \(\dpi{120} \varepsilon\).
1. ამ ამოცანის ნახაზს მოვიყვანთ ოდნავ ქვევით, მას მერე რაც ჩავატარებთ ველის სტრუქტურის ანალიზს და შევარჩევთ 2 ზედაპირებს.
2. ამ შემთხვევაში მუხტის განაწილებას აქვს „ღერძული სიმეტრია“.
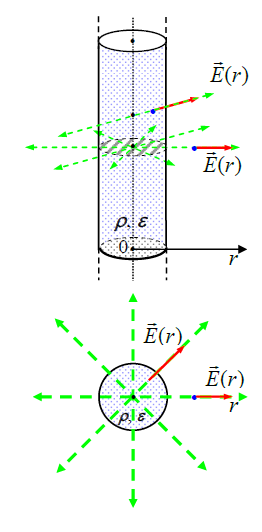
ასეთი სიმეტრია გვკარნახობს ელექტრული ველის შესაბამის სტრუქტურას - ნახაზზე წყვეტილი ხაზებით გამოსახულია ამ ველის ძალწირები ძელაკის ღერძისადმი მართობულ ერთერთ სიბრტყეში. ეს არის ცენტრიდან ყველა მიმართულებით გამომავალი რადიალური სხივები (განსაზღვრულობისათვის მუხტს ვთვლით დადებითად. სივრცის ნებისმიერ წერტილში (ძელაკის როგორც შიგნით, ისე გარეთ) დაძაბულობის ვექტორი მართობულია ძელაკის ღერძისადმი და მიმართულია რადიალურად. დაძაბულობის მოდული, ისევე როგორც წინა მაგალითში, შეიძლება იყოს დამოკიდებული ღერძიდან r დაშორებაზე, მაგრამ არავითარ შემთხვევაში არ იქნება დამოკიდებული აზიმუტურ მიმართულებაზე. ნახაზზე ამას აღვნიშნავთ ასე \(\dpi{120} \vec{E}\left ( r \right )\) (აქაც ფრჩხილებში არის მოდული r).
3. \(\dpi{120} \Sigma\) შეკრული ზედაპირის კრიტერიუმს ამ შემთხვევაში აკმაყოფილებს სწორი წრიული ცილინდრი, რომელიც კოაქსიალურია (ღერძები თანხვედრილია) ძელაკთან. ცილინდრის სიმაღლე ირჩევა ნებისმიერად და აღვნიშნოთ h-ით. ძელაკის გარეთ და შიგნით ველის საპოვნელად კვლავ დაგვჭირდება ორი ჩაკეტილი ზედაპირი – 2. მათ შორის განსხვავება არის მხოლოდ ის, რომ პირველის რადიუსი r > R , ხოლო მეორესი r < R (ამას გარდა, მხოლოდ და მხოლოდ ვიზუალური ეფექტისთვის ნახაზზე ოდნავ განსხვავებული სიმაღლეები აქვს ცილინდრებს). კვლავ მივაქციოთ ყურადღება, რომ ცილინდრების გვერდითა ზედაპირები
r-ის ნებისმიერი მნიშვნელობისთვის. ყოველი ზედაპირო
2 შედგება ამ შემთხვევაში თავის მხრივ ორი ნაწილისგან – გვერდითა ზედაპირისაგან
base.
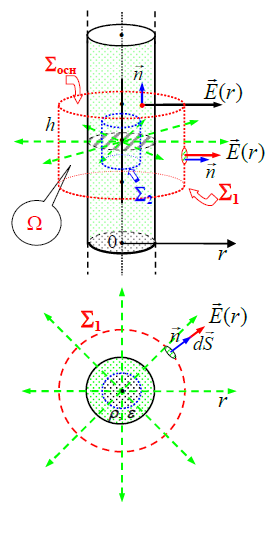
ნახაზზე უნდა მივუთითოთ დაძაბულობის ვექტორი და \(\dpi{120} \vec{n}\) ნორმალი ვექტორი (ან 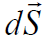 ) ისევ და ისევ ზედაპირის იმ მცირე dS ელემენტებისთვის.
) ისევ და ისევ ზედაპირის იმ მცირე dS ელემენტებისთვის.
ელემენტები უნდა აირჩეს ნებისმიერ დაშორებაზე ძელაკის ღერძიდან ორივე ზედაპირისთვის (2) როგორც გვერდითა ზედაპირებზე ასევე ფუძეებზე.
4.  სახის ზედაპირული ინტეგრალის გამოთვლის პროცედურა არანაირად არ განსხვავდება
სახის ზედაპირული ინტეგრალის გამოთვლის პროცედურა არანაირად არ განსხვავდება 2 შემთხვევებისთვის. ამიტომ „1“ და „2“ ინდექსებს გამოთვლებისას არ გამოვიყენებთ. დავყოთ ის ორ ნაწილად - გვერდითა ზედაპირი და ფუძეების ზედაპირი:
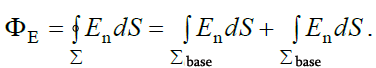
უწინარესად გავითვალისწინოთ, რომ ფუძეებზე 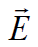 და \(\dpi{120} \vec{n}\) ვექტორები ურთიერთმართობია, ამიტომ ინტეგრალქვეშა გამოსახულება ნულის ტოლია ამ ზედაპირის ნებისმიერი მცირე ელემენტისთვის (Еn = 0). ანუ მთელი ინტეგრალიც
და \(\dpi{120} \vec{n}\) ვექტორები ურთიერთმართობია, ამიტომ ინტეგრალქვეშა გამოსახულება ნულის ტოლია ამ ზედაპირის ნებისმიერი მცირე ელემენტისთვის (Еn = 0). ანუ მთელი ინტეგრალიც 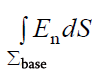 არ იძლევა არავითარ წვლილს ნაკადში S ზედაპირში. გვერდითა
არ იძლევა არავითარ წვლილს ნაკადში S ზედაპირში. გვერდითა და \)\dpi{120} \vec{n}\( თანხვედრო მიმართულებისაა და ამიტომ
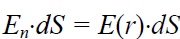 . Е(r) დაძაბულობის მოდული მუდმივია ცილინდრის გვერდითა ზედაპირზე. შეგვიძლია მისი გატანა ინტეგრალიდან:
. Е(r) დაძაბულობის მოდული მუდმივია ცილინდრის გვერდითა ზედაპირზე. შეგვიძლია მისი გატანა ინტეგრალიდან:
.\)\oint_{\Sigma _{wall}}^{ }E_{n}dS=E(r)\oint_{\Sigma _{wall}}^{ }dS=E(r)S_{wall}\(
ინტეგრალი 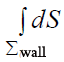 არის
არის
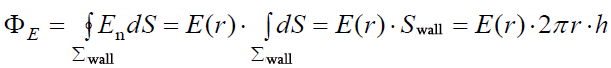 .
.
ამდენად, შევძელით ზედაპირული ინტეგრალი წარმოგვედგინა სკალარული სიდიდეების ნამრავლის სახით. გარეგნულად ის ერთნაირია 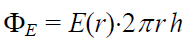
განსხვავება არის მათ მიკუთვნებაში r -ის ამა თუ იმ დიაპაზონზე მიკუთვნებაში: r > R და r < R.
5. ა) პირველ შემთხვევაში (r > R) 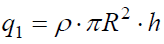 .
.
( \)\dpi{120} \pi R^{2}h\( - სიმაღლის სწორი წრიული ცილინდრის მოცულობაა).
ბ) 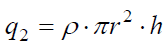 .
.
6. ახლა უკვე გაუსის თეორემის თანახმად შეიძლება ჩავწეროთ ორი ტოლობა.

ა) ვასკვნით, რომ ძელაკის გარეთ ველის დაძაბულობა იცვლება კანონით:
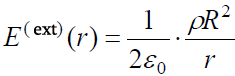 როცა r > R (ველი ძელაკის გარეთ).
როცა r > R (ველი ძელაკის გარეთ).
ამდენად, ძელაკის გარეთ ველი არის რადიალური მიმართულების და დამუხტული ძელაკის ღერძიდან დაშორების უკუპროპორციულია.

ბ) 
აქედან ვღებულობთ, რომ ძელაკის შიგნით ველი იცვლება კანონით:
 , როცა r ≤ R (ველი ძელაკის შიგნით).
, როცა r ≤ R (ველი ძელაკის შიგნით).
ძელაკის შიგნით ველი იზრდება წრფივად ძელაკის ღერძიდან დაშორებით. შედეგები წარმოდგენილია ნახაზზე.
დასკვნისთვის შევნიშნოთ, რომ არსებითი მომენტი ანალოგიური ამოცანების გადაჭრაში არის ტიპის ზედაპირული ინტეგრალის შეცვლა სკალარული სიდიდეების ნამრავლით, რაც ზოგად შემთხვევაში შეუძლებელია და შესაძლებელია მხოლოდ სამი ტიპის სიმეტრიების შემთხვევებში – სფერული, ძერძული («აქსიალური») ან ბრტყელი («ბილატერალური» ანუ «სარკული»). დამუხტული სხეულის ნებისმიერი ფორმისთვის ერთადერთი შესაძლებლობა არის „პირველი“ მეთოდის გამოყენება, რომელიც უშუალოდ სუპერპოზიციის პრინციბს ეყრდნობა ან კიდევ ექსპერიმენტული გაზომვა.
ჩამოვაყალიბოთ თეორემა.
♦ ვაკუუმში ნებისმიერ ზედაპირში ელექტროსტატიკური ველის დაძაბულობის ვექტორის ნაკადი ამ ზედაპირის შიგნით მოთავსებული მუხტების ჯამური მუხტის პროპორციულია.
Si სისტემაში პროპორციულობის კოეფიციენტი ტოლია 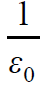 .
.
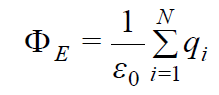 (16.5)
(16.5)
ნაკადის განსაზღვრების გათვალისწინებით შეგვიძლია (16.5) ასე ჩავწეროთ:
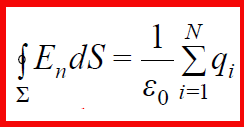 (16.6)
(16.6)
მივყვეთ ნაბიჯ-ნაბიჯ გაუსის თეორემის დამტკიცებას. დავიწყოთ უმარტივესი შემთხვევით:
► ა) სფერული ზედაპირის ცენტრში მოთავსებულია წერტილოვანი მუხტი
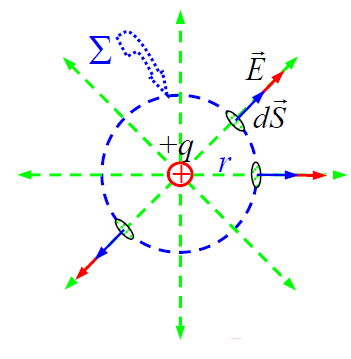
გამოვთვალოთ დაძაბულობის ვექტორის ნაკადი. წერტილოვანი მუხტის ველის სტრუქტურა უკვე კარგად ვიცით - სივრცის ნებისმიერ წერტილში დაძაბულობის ვექტორს აქვს რადიალური მიმართულება, ხოლო მისი სიდიდე ველის წყარო წერტილოვანი მუხტისგან დაშორების კვადრატის უკუპროპორციულია. უწინარეს ყოვლისა, აღვნიშნოთ, რომ სფერული ზედაპირის ნებისმიერი მცირე ელემენტისთვის 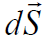 და
და 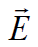 ვექტორების მიმართულებები ერთმანეთს ემთხვევა. ეს საშუალებას გვაძლევს ინტეგრალის ქვეშ გადავიდეთ En ვექტორის პროექციიდან მის მოდულზე E(r):
ვექტორების მიმართულებები ერთმანეთს ემთხვევა. ეს საშუალებას გვაძლევს ინტეგრალის ქვეშ გადავიდეთ En ვექტორის პროექციიდან მის მოდულზე E(r):
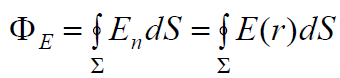
ჩავსვათ წერტილოვანი მუხტის ველის დაძაბულობის ცნობილი გამოსახულება (15.5)-დან:
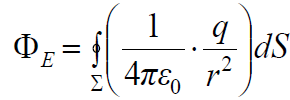
ინტეგრალქვეშა გამოსახულება მუდმივია ინტეგრების მთელი \(\dpi{120} \Sigma\) ზედაპირის ფარგლებში, ამიტომ შეგვიძლია მისი გამოტანა ინტეგრალს გარეთ. დარჩენილი ინტეგრალი არის \(\dpi{120} \Sigma\) ფართობი, იგი სფეროსათვის არის, როგორც ცნობილია, 4πr2. შედეგად საპოვნელი ნაკადისთვის ვიღებთ:
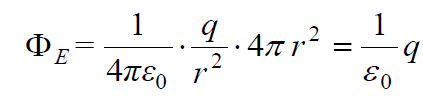
► ბ) წავანაცვლოთ წერტილოვანი მუხტი იგივე სფეროს ცენტრიდან.
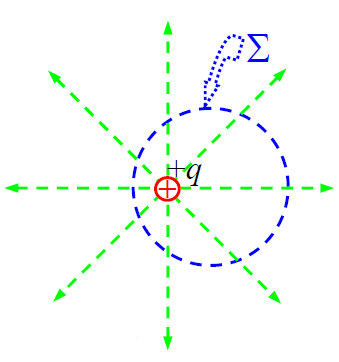
ნაკადის ზედაპირული ინტეგრალის გამოთვლა მნიშვნელოვნად რთულდება. ახლა ყოველი მცირე ელემენტური ზედაპირისთვის კუთხე 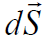 და
და 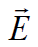 ვექტორებს შორის განსხვავებულია, ისევე როგორც განსხვავებულ მნიშვნელობებს იღებს დაძაბულობის მოდულიც. მიუხედავად ამ სირთულეებისა ოდნავ ქვემოთ გამოვთვლით ამ ინტეგრალს მკაცრად მათემატიკურად.
ვექტორებს შორის განსხვავებულია, ისევე როგორც განსხვავებულ მნიშვნელობებს იღებს დაძაბულობის მოდულიც. მიუხედავად ამ სირთულეებისა ოდნავ ქვემოთ გამოვთვლით ამ ინტეგრალს მკაცრად მათემატიკურად.
ნახაზი გვეხმარება დავინახოთ, რომ განსახილველი ნაკადი არაფრით არ შეცვლილა „ა“ შემთხვევასთან შედარებით. გავიხსენოთ, ნაკადი ზედაპირში პროპორციულია ამ ზედაპირის გამჭოლი ძალწირების რაოდენობის. ეს რაოდენობა, ცხადია, არ შეცვლილა მუხტის ცენტრიდან წანაცვლებით. ამიტომ შეიძლება ვიგულისხმოთ, რომ გაუსის თეორემაც ძალაში რჩება. ნაკადის მკაცრად მათემატიკურად გამოსაყვანად, (16.6) ინტდეგრალქვეშა გამოსახულებაში სკალარული ნამრავლი ჩავწეროთ რამდენადმე სხვა ფორმით:
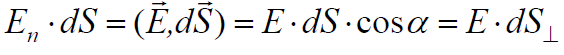
აღნიშვნა 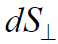 გამოყენებულია ვექტორის ველის დაძაბულობის მიმართულებაზე პროექციის გამოსახატად. dS-ის cosa -ზე გადამრავლებით ხომ მიიღება იმ სფეროს მცირე ელემენტის ფართობი, რომლის რადიუსი არის r და ცენტრი კი მუხტის მდებარეობას ემთხვევა. ეს ელემენტი მართობულია
გამოყენებულია ვექტორის ველის დაძაბულობის მიმართულებაზე პროექციის გამოსახატად. dS-ის cosa -ზე გადამრავლებით ხომ მიიღება იმ სფეროს მცირე ელემენტის ფართობი, რომლის რადიუსი არის r და ცენტრი კი მუხტის მდებარეობას ემთხვევა. ეს ელემენტი მართობულია 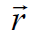 რადიუს-ვექტორისა, რომელიც გავლებულია მუხტიდან ზედაპირის ელემენტისკენ. ჩავსვათ ველის დაძაბულობის გამოსახულება წერტილოვანი მუხტისთვის (15.5)-დან.
რადიუს-ვექტორისა, რომელიც გავლებულია მუხტიდან ზედაპირის ელემენტისკენ. ჩავსვათ ველის დაძაბულობის გამოსახულება წერტილოვანი მუხტისთვის (15.5)-დან.
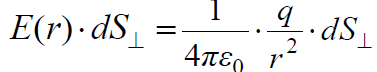
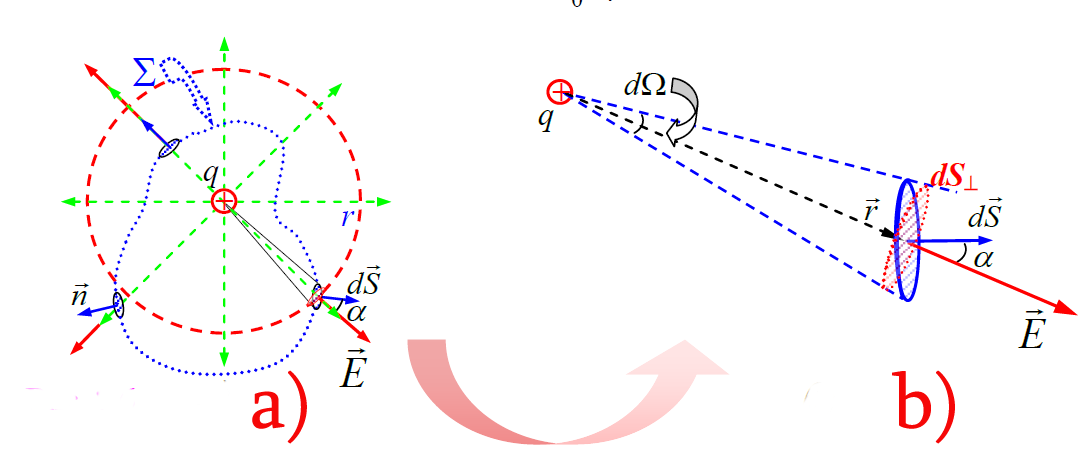
მათემატიკიდან ვიცით, რომ ფარდობა 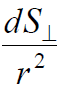 არის ზომა სხეულოვანი კუთხისა dΩ, რომელიც ეყრდნობა
არის ზომა სხეულოვანი კუთხისა dΩ, რომელიც ეყრდნობა 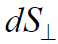 ფართობის მქონე r რადიუსიანი სფერული ზედაპირის ელემენტს. ამდენად საპოვნელი ნაკადის გამოსახულება შეიძლება ასე ჩავწეროთ:
ფართობის მქონე r რადიუსიანი სფერული ზედაპირის ელემენტს. ამდენად საპოვნელი ნაკადის გამოსახულება შეიძლება ასე ჩავწეროთ:
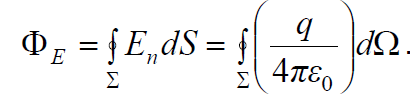
ინტეგრალქვეშა გამოსახულება, ცხადია მუდმივი სიდიდეა, ხოლო სხეულოვანი კუთხე ჩაკეტილი ზედაპირის შემოვლისას იცვლება ფარგლებში 0-დან 4π-მდე. ამის გათვალისწინებით მივდივართ უკვე ცნობილ შედეგამდე:
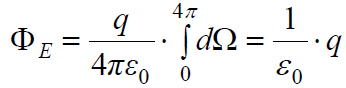
დავრწმუნდით რა, რომ ძალწირების თვისებაზე დაყრდნობა („ნაკადი პროპორციულია ძალწირების რაოდენობის ...“) გვაძლევს სამართლიან შედეგს, დამტკიცების შემდგომი ნაბიჯების დასაბუთებისთვის გამოვიყენებთ სწორედ ამ მიდგომას.
► გ) ნებისმიერი ფორმის ჩაკეტილი ზედაპირი მოიცავს ერთ წერტილოვან მუხტს.
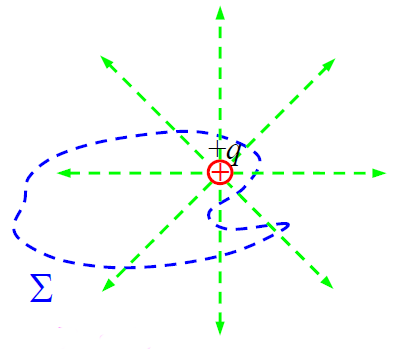
ნახაზზე ჩანს, რომ \(\dpi{120} \Sigma\) ზედაპირიდან გამომავალი ძალწირების (გამომავალი, რადგან დადებითი მუხტია არჩეული) რაოდენობა არ იცვლება მუხტის მომცველი თუნდა ყველაზე უცნაური ფორმების, მაგალითად, ფენოვანი ჩაკეტილი ზედაპირების შემთხვევაშიც კი. მიუხედავად იმისა, რომ ძალწირ უკანასკნელ შემთხვევაში შეუძლია რამდენჯერმე გადაკვეთო \(\dpi{120} \Sigma\) ზედაპირი, მისი ჯამური წვლილი ყოველთვის იქნება „+1“. ნახაზზე შეგვიძლია დავინახოთ, რომ „გამოსვლების“ რაოდენობა ყოველთვის ერთით მეტია „შესვლების“ რაოდენობაზე. ამდენად, ამ შემთხვევაშიც ნაკადი \(\dpi{120} \Sigma\) ზედაპირის შიგნით მდებარე მუხტის პროპორციულია.
► დ) ერთი წერტილოვანი მუხტი მოთავსებულია ნებისმიერი ფორმის ჩაკეტილი ზედაპირის გარეთ.
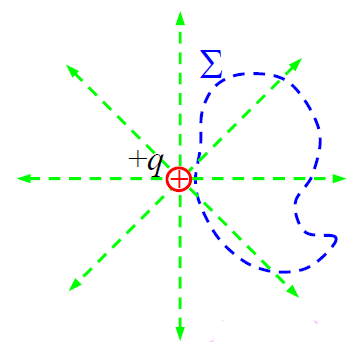
ნახაზიდან კარგად ჩანს, რომ ყოველი ძალწირისთვის მისი \(\dpi{120} \Sigma\) ზედაპირთან გადაკვეთის რიცხვი ყოველთვის ლუწია - „შიგნით“ შესვლის რიცხვი ტოლია „გარეთ“ გამოსვლის რიცხვისა. ამიტომ \(\dpi{120} \Sigma\) ჩაკეტილი ზედაპირის გარეთ მყოფი q მუხტი არ წარმოშობს ამ ზედაპირში დამატებით ნაკადს.
გამოვიყენოთ მიღებული შედეგები ყველაზე ზოგად შემთხვევაში.
► ე) N წერტილოვანი მუხტების სისტემა q1, q2, ..., qi, ..., qN (ან დამუხტული სხეულების სისტემა) მდებარეობს \(\dpi{120} \Sigma\) ნებისმიერი ფორმის ჩაკეტილი ზედაპირის როგორც შიგნით, ასევე გარეთ.
\(\dpi{120} \Sigma\) ჩაკეტილი ზედაპირის შიგნით მდებარე ყოველი qi მუხტისთვის დამტკიცებულია, რომ მის მიერ შექმნილი ნაკადი ჩაკეტილ ზედაპირში ტოლია
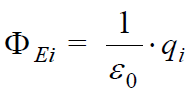
ამავდროულად ნებისმიერი გარეთ მყოფი qk მუხტი არ წარმოშობს ამ ზედაპირში ნაკადს. ადრე დასაბუთებული ნაკადის სუპერპოზიციის პრინციპის გამოყენებით შეგვიძლია დავწეროთ:
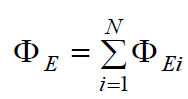
ამის გათვალისწინებით შეგვიძლია ვამტკიცოთ, რომ ზედაპირში სრული ნაკადი შიგნით მოთავსებული მუხტების ალგებრული ჯამის პროპორციულია:
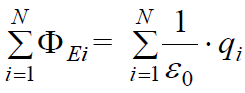 ანუ
ანუ 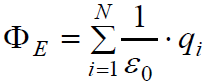
♦ აქვე შენიშვნა
1. ტექნიკური თვალსაზრისით გაუსის თეორემის ანალიტიკური ჩაწერა რამდენადმე იცვლება იმისდა მიხედვით თუ მუხტების რა სახის განაწილება გვაქვს. იმისათვის, რათა ვიპოვოთ «\(\dpi{120} \Sigma\) ზედაპირით შემოფარგლულ \(\dpi{120} \Omega\) სივრცეში მოქცეული მუხტების ალგებრული ჯამი» უნდა გამოვიყენოთ ინტეგრების პროცედურა. მარჯვენა ნაწილში ჯამის ნაცვლად გაჩნდება შესაბამისი ინტეგრალი - წირითი, ზედაპირული ან მოცულობითი:
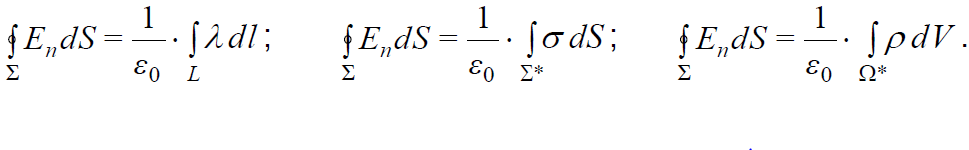
აქ \(\dpi{120} \lambda\), \(\dpi{120} \sigma\) და \(\dpi{120} \rho\) – ჩვენთვის უკვე ცნობილი მუხტის წრფივი, ზედაპირული და მოცულობითი სიმკვრივეებია შესაბამისად, ხოლო “L”, “\(\dpi{120} \Sigma\)*” და “\(\dpi{120} \Omega\)” – სხეულებია (სივრცის ნაწილები), რომელშიც არის მუხტი განაწილებული (ერთგანზომილებიანი, ორგანზომილებიანი და სამგანზომილებიანი).
2. კიდევ ერთხელ აღვნიშნოთ, რომ გაუსის თეორემა არის კულონის კანონისა და ძაბვის სუპერპოზიციის პრინციპის შედეგი.
ვთქვათ გვაქვს რაღაც \(\dpi{120} \Sigma\) ზედაპირი. დავყოთ ეს ზედაპირი მცირე ელემენტებად და თითოეულ ელემენტს შევუსაბამოთ ვექტორი 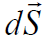 . ასეთი ვექტორის მოდული ტოლია ზედაპირის ელემენტის dS ფართობისა, მიმართულება კი ემთხვევა ამ ზედაპირის
. ასეთი ვექტორის მოდული ტოლია ზედაპირის ელემენტის dS ფართობისა, მიმართულება კი ემთხვევა ამ ზედაპირის 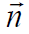 ნორმალის მიმართულებას (რათქმაუნდა უნდა ავარჩიოთ ნორმალის „დადებითი“ მიმართულებაც).
ნორმალის მიმართულებას (რათქმაუნდა უნდა ავარჩიოთ ნორმალის „დადებითი“ მიმართულებაც).
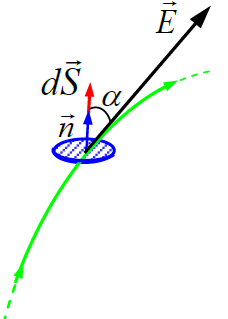
dS ელემენტურ ზედაპირში 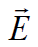 ვექტორის ელემენტური ნაკადი dФ ეწოდება სიდიდეს:
ვექტორის ელემენტური ნაკადი dФ ეწოდება სიდიდეს:
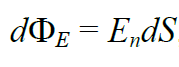 (16.1)
(16.1)
სადაც En – არის 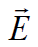 ვექტორის პროექცია
ვექტორის პროექცია 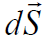 ელემენტური ზედაპირის დადებით
ელემენტური ზედაპირის დადებით 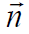 ნორმალზე.
ნორმალზე.
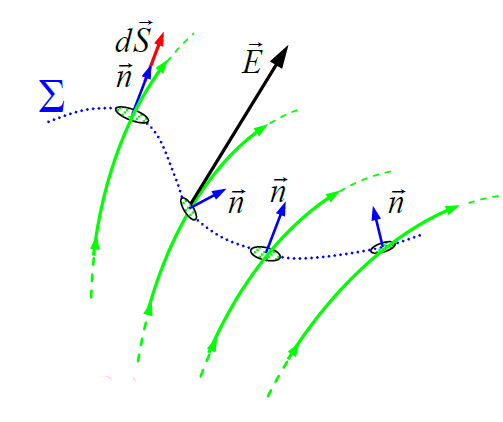 განსაზღვრებიდან ჩანს, რომ ელემენტური ნაკადი - ეს არის უბრალოდ
განსაზღვრებიდან ჩანს, რომ ელემენტური ნაკადი - ეს არის უბრალოდ 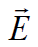 და
და 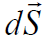 ვექტორების სკალარული ნამრავლი. ამიტომ შეგვიძლია ასევე გამოვიყენოთ ამ სიდიდის ასეთი მათემატიკური ჩაწერა:
ვექტორების სკალარული ნამრავლი. ამიტომ შეგვიძლია ასევე გამოვიყენოთ ამ სიდიდის ასეთი მათემატიკური ჩაწერა:
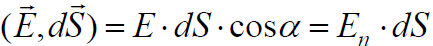
ახლა ადვილია განვსაზღვროთ 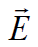 ვექტორული ველის სრული ნაკადი (ან უბრალოდ ნაკადი) ნებისმიერ \(\dpi{120} \Sigma\) ზედაპირში. ეს არის უბრალოდ ჯამი ყველა ელემენტური ნაკადებისა ამ ზედაპირის ელემენტურ ზედაპირებში. რადგან ელემენტური ზედაპირები იგულისხმება ფიზიკურად უსასრულოდ მცირე ზომების მქონედ, ამიტომ უსასრულოდ ბევრი შესაკრების აჯამვა მოგვიწევს. მათემატიკურად ასეთი ზღვრული გადასვლა ნიშნავს \(\dpi{120} \Sigma\) ზედაპირზე ინტეგრებას:
ვექტორული ველის სრული ნაკადი (ან უბრალოდ ნაკადი) ნებისმიერ \(\dpi{120} \Sigma\) ზედაპირში. ეს არის უბრალოდ ჯამი ყველა ელემენტური ნაკადებისა ამ ზედაპირის ელემენტურ ზედაპირებში. რადგან ელემენტური ზედაპირები იგულისხმება ფიზიკურად უსასრულოდ მცირე ზომების მქონედ, ამიტომ უსასრულოდ ბევრი შესაკრების აჯამვა მოგვიწევს. მათემატიკურად ასეთი ზღვრული გადასვლა ნიშნავს \(\dpi{120} \Sigma\) ზედაპირზე ინტეგრებას:
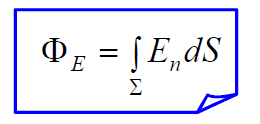 (16.2)
(16.2)
► აქვე გავაკეთოთ ორი შენიშვნა „დაძაბულობის ვექტორი ნაკადზე“
1. თუ დაცულია პირობა – ძალხაზების სიმჭიდროვე პროპორციულია ველის დაძაბულობის მოდულისა, მაშინ სამართლიანია ასევე შემდეგი მნიშვნელოვანი მტკიცება: მოცემულ ზედაპირში დაძაბულობის ვექტორის ნაკადი პროპორციულია ამ ზედაპირში გამავალი ძალხაზების რიცხვისა. ამას შემდგომში გამოვიყენებთ გაუსის თეორემის დამტკიცებისას.
აქვე უნდა შევთანხმდეთ, რომ რადგან დაძაბულობის ვექტორის ნაკადი არის ალგებრული სიდიდე და მან შეიძლება მიიღოს როგორც დადებითი ასევე უარყოფითი მნიშვნელობებიც (იმის მიხედვით თუ რა მიმართულებით კვეთს ზედაპირს ძალწირები), ამიტომ ძალწირების რაოდენობაც დაითვალოს მიმართულების მიხედვით. ჩაკეტილი ზედაპირებისთვის დადებითად ჩაითვალოს ნორმალი რომელიც მიმართულია გარეთ და შესაბამისად ძალწირები რომლებიც გამოდიან გარეთ სათვალავში ავიღოთ „+“ ნიშნით, ხოლო, რომლებიც შედიან შიგნით - „-„ ნიშნით.
2. ნაკადებისთვის სუპერპოზიციის პრინციპი
ვთქვათ რაღაც \(\dpi{120} \Sigma\) ზედაპირში ნაკადი წარმოქმნილია N რაოდენობის qi მუხტების მიერ: q1, q2, ..., qi, ..., qN. ვაჩვენოთ, რომ \(\dpi{120} \Phi _{E}\) სრული ნაკადი ამ შემთხვევაში ცალკეული ნაწილაკის მიერ წარმოქმნილი \(\dpi{120} \Phi _{Ei}\) ნაკადების ალგებრული ჯამის ტოლია. ყველა დამუხტული ნაწილაკის ველის სრული ნაკადი გამოითვლება ასე:
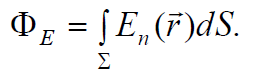
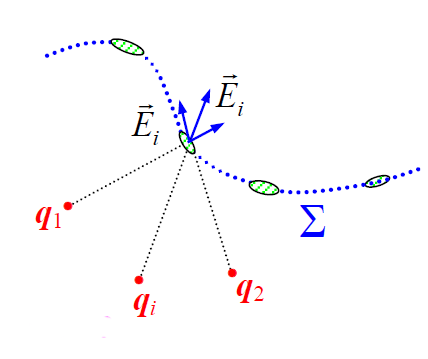 ელექტრული ველის დაძაბულობის
ელექტრული ველის დაძაბულობის 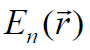 ნორმალური ვექტორისთვის სუპერპოზიციის პრინციპის გამოყენებით ვწერთ
ნორმალური ვექტორისთვის სუპერპოზიციის პრინციპის გამოყენებით ვწერთ
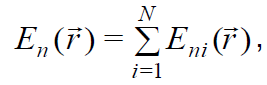
ჩავსვათ ნაკადის გამოსახულებაში და ადგილები შევუცვალოთ ჯამსა და ინტეგრალს
.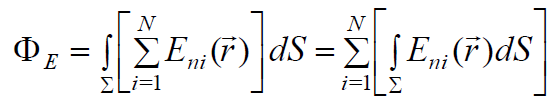
აქ 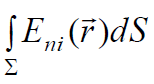 თითოეული დამუხტული ნაწილაკის მიერ S ზედაპირში წარმოქმნილი ნაკადი FЕi. მივედით მნიშვნელოვან დასკვნამდე, რომ მუხტების სისტემის ველის დაძაბულობის ნაკადი ცალკეული მუხტების ნაკადების ალგებრული ჯამის ტოლია:
თითოეული დამუხტული ნაწილაკის მიერ S ზედაპირში წარმოქმნილი ნაკადი FЕi. მივედით მნიშვნელოვან დასკვნამდე, რომ მუხტების სისტემის ველის დაძაბულობის ნაკადი ცალკეული მუხტების ნაკადების ალგებრული ჯამის ტოლია:
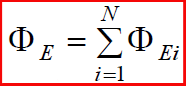 (16.3)
(16.3)
ამ შედეგს ასევე გამოვიყენებთ გაუსის თეორემის დასასაბუთებლად.


