ჩამოვაყალიბოთ თეორემა.

♦ ვაკუუმში ნებისმიერ ზედაპირში ელექტროსტატიკური ველის დაძაბულობის ვექტორის ნაკადი ამ ზედაპირის შიგნით მოთავსებული მუხტების ჯამური მუხტის პროპორციულია.

Si სისტემაში პროპორციულობის კოეფიციენტი ტოლია .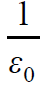

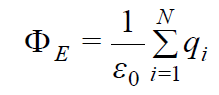                            (16.5)

ნაკადის განსაზღვრების გათვალისწინებით შეგვიძლია (16.5) ასე ჩავწეროთ:

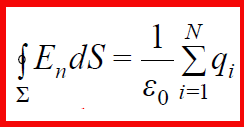             (16.6)

მივყვეთ ნაბიჯ-ნაბიჯ გაუსის თეორემის დამტკიცებას. დავიწყოთ უმარტივესი შემთხვევით:

► ა) სფერული ზედაპირის ცენტრში მოთავსებულია წერტილოვანი მუხტი

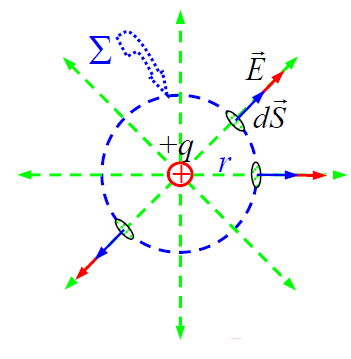
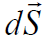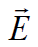გამოვთვალოთ დაძაბულობის ვექტორის ნაკადი. წერტილოვანი მუხტის ველის სტრუქტურა უკვე კარგად ვიცით - სივრცის ნებისმიერ წერტილში დაძაბულობის ვექტორს აქვს რადიალური მიმართულება, ხოლო მისი სიდიდე ველის წყარო წერტილოვანი მუხტისგან დაშორების კვადრატის უკუპროპორციულია. უწინარეს ყოვლისა, აღვნიშნოთ, რომ სფერული ზედაპირის ნებისმიერი მცირე ელემენტისთვის  და  ვექტორების მიმართულებები ერთმანეთს ემთხვევა. ეს საშუალებას გვაძლევს ინტეგრალის ქვეშ გადავიდეთ  E_n  ვექტორის პროექციიდან მის მოდულზე E(r):

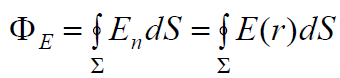
ჩავსვათ წერტილოვანი მუხტის ველის დაძაბულობის ცნობილი გამოსახულება (15.5)-დან:

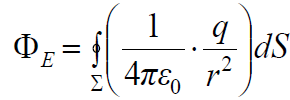
ინტეგრალქვეშა გამოსახულება მუდმივია ინტეგრების მთელი \(\dpi{120} \Sigma\) ზედაპირის ფარგლებში, ამიტომ შეგვიძლია მისი გამოტანა ინტეგრალს გარეთ. დარჩენილი ინტეგრალი არის \(\dpi{120} \Sigma\) ფართობი, იგი სფეროსათვის არის, როგორც ცნობილია, 4πr². შედეგად საპოვნელი ნაკადისთვის ვიღებთ:

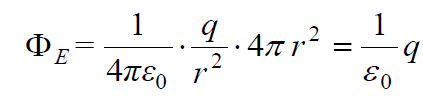
► ბ) წავანაცვლოთ წერტილოვანი მუხტი იგივე სფეროს ცენტრიდან.

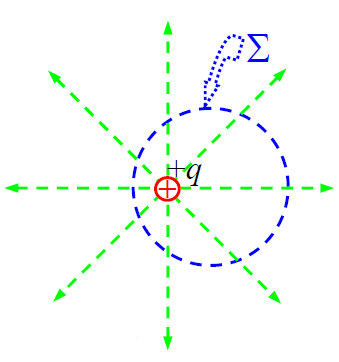
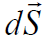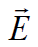ნაკადის ზედაპირული ინტეგრალის გამოთვლა მნიშვნელოვნად რთულდება. ახლა ყოველი მცირე ელემენტური ზედაპირისთვის  კუთხე   და  ვექტორებს შორის განსხვავებულია, ისევე როგორც განსხვავებულ მნიშვნელობებს იღებს დაძაბულობის მოდულიც. მიუხედავად ამ სირთულეებისა ოდნავ ქვემოთ გამოვთვლით ამ ინტეგრალს მკაცრად მათემატიკურად.

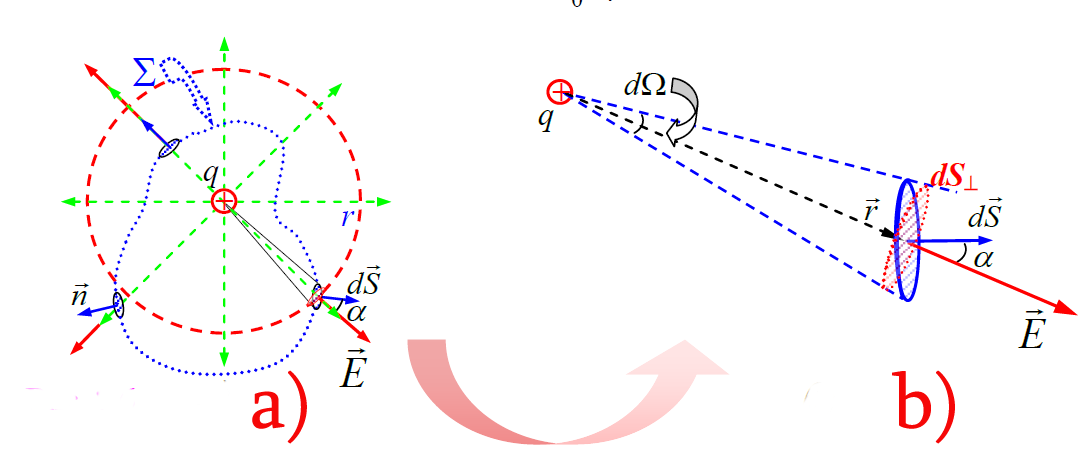
ნახაზი გვეხმარება დავინახოთ, რომ განსახილველი ნაკადი არაფრით არ შეცვლილა „ა“ შემთხვევასთან შედარებით. გავიხსენოთ, ნაკადი ზედაპირში პროპორციულია ამ ზედაპირის გამჭოლი ძალწირების რაოდენობის. ეს რაოდენობა, ცხადია, არ შეცვლილა მუხტის ცენტრიდან წანაცვლებით.  ამიტომ შეიძლება ვიგულისხმოთ, რომ გაუსის თეორემაც ძალაში რჩება. ნაკადის მკაცრად მათემატიკურად გამოსაყვანად, (16.6) ინტდეგრალქვეშა გამოსახულებაში სკალარული ნამრავლი ჩავწეროთ რამდენადმე სხვა ფორმით:

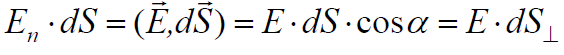
აღნიშვნა 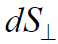  გამოყენებულია    ვექტორის ველის დაძაბულობის მიმართულებაზე პროექციის გამოსახატად. dS-ის cosa -ზე გადამრავლებით ხომ მიიღება იმ სფეროს მცირე ელემენტის ფართობი, რომლის რადიუსი არის r და ცენტრი კი მუხტის მდებარეობას ემთხვევა. ეს ელემენტი მართობულია  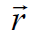  რადიუს-ვექტორისა, რომელიც გავლებულია მუხტიდან ზედაპირის ელემენტისკენ. ჩავსვათ ველის დაძაბულობის გამოსახულება წერტილოვანი მუხტისთვის (15.5)-დან.

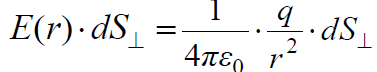
მათემატიკიდან ვიცით, რომ ფარდობა 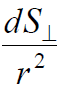  არის ზომა სხეულოვანი კუთხისა dΩ, რომელიც ეყრდნობა 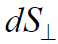ფართობის მქონე r  რადიუსიანი სფერული ზედაპირის ელემენტს. ამდენად საპოვნელი ნაკადის გამოსახულება შეიძლება ასე ჩავწეროთ: 

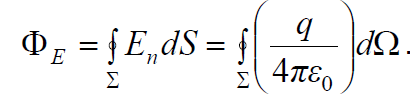
ინტეგრალქვეშა გამოსახულება, ცხადია მუდმივი სიდიდეა, ხოლო სხეულოვანი კუთხე ჩაკეტილი ზედაპირის შემოვლისას იცვლება ფარგლებში 0-დან 4π-მდე. ამის გათვალისწინებით მივდივართ უკვე ცნობილ შედეგამდე:

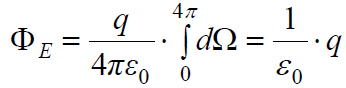
დავრწმუნდით რა, რომ ძალწირების თვისებაზე დაყრდნობა („ნაკადი პროპორციულია ძალწირების რაოდენობის ...“) გვაძლევს სამართლიან შედეგს, დამტკიცების შემდგომი ნაბიჯების დასაბუთებისთვის გამოვიყენებთ სწორედ ამ მიდგომას.

► გ) ნებისმიერი ფორმის ჩაკეტილი ზედაპირი მოიცავს ერთ წერტილოვან მუხტს.

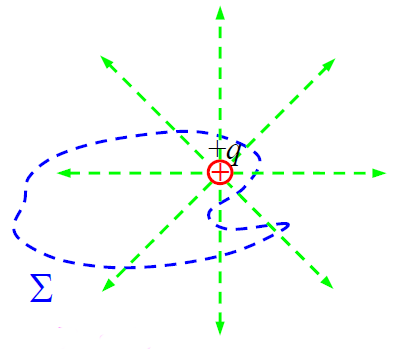
ნახაზზე ჩანს, რომ \(\dpi{120} \Sigma\) ზედაპირიდან გამომავალი ძალწირების (გამომავალი, რადგან დადებითი მუხტია არჩეული) რაოდენობა არ იცვლება მუხტის მომცველი თუნდა ყველაზე უცნაური ფორმების, მაგალითად, ფენოვანი ჩაკეტილი ზედაპირების შემთხვევაშიც კი. მიუხედავად იმისა, რომ ძალწირ უკანასკნელ შემთხვევაში შეუძლია რამდენჯერმე გადაკვეთო \(\dpi{120} \Sigma\) ზედაპირი, მისი ჯამური წვლილი ყოველთვის იქნება „+1“. ნახაზზე შეგვიძლია დავინახოთ, რომ „გამოსვლების“ რაოდენობა ყოველთვის ერთით მეტია „შესვლების“ რაოდენობაზე. ამდენად, ამ შემთხვევაშიც ნაკადი \(\dpi{120} \Sigma\) ზედაპირის შიგნით მდებარე მუხტის პროპორციულია.

► დ) ერთი წერტილოვანი მუხტი მოთავსებულია ნებისმიერი ფორმის ჩაკეტილი ზედაპირის გარეთ.

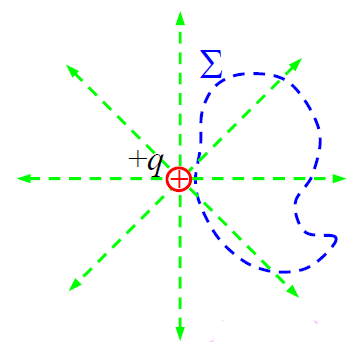
ნახაზიდან კარგად ჩანს, რომ ყოველი ძალწირისთვის მისი \(\dpi{120} \Sigma\) ზედაპირთან გადაკვეთის რიცხვი ყოველთვის ლუწია - „შიგნით“ შესვლის რიცხვი ტოლია „გარეთ“ გამოსვლის რიცხვისა. ამიტომ \(\dpi{120} \Sigma\) ჩაკეტილი ზედაპირის გარეთ მყოფი q მუხტი არ წარმოშობს ამ ზედაპირში დამატებით ნაკადს.

გამოვიყენოთ მიღებული შედეგები ყველაზე ზოგად შემთხვევაში.

►​ ე) N წერტილოვანი მუხტების სისტემა q₁, q₂, ..., q_i, ..., q_N (ან დამუხტული სხეულების სისტემა) მდებარეობს \(\dpi{120} \Sigma\) ნებისმიერი ფორმის ჩაკეტილი ზედაპირის როგორც შიგნით, ასევე გარეთ.

\(\dpi{120} \Sigma\) ჩაკეტილი ზედაპირის შიგნით მდებარე ყოველი q_i მუხტისთვის დამტკიცებულია, რომ მის მიერ შექმნილი ნაკადი ჩაკეტილ ზედაპირში ტოლია

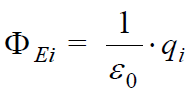
ამავდროულად ნებისმიერი გარეთ მყოფი q_k მუხტი არ წარმოშობს ამ ზედაპირში ნაკადს. ადრე დასაბუთებული ნაკადის სუპერპოზიციის პრინციპის გამოყენებით შეგვიძლია დავწეროთ:

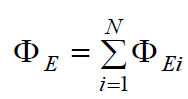
ამის გათვალისწინებით შეგვიძლია ვამტკიცოთ, რომ ზედაპირში სრული ნაკადი შიგნით მოთავსებული მუხტების ალგებრული ჯამის პროპორციულია:

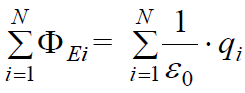 ანუ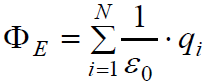  

♦ აქვე შენიშვნა

1. ტექნიკური თვალსაზრისით გაუსის თეორემის ანალიტიკური ჩაწერა რამდენადმე იცვლება იმისდა მიხედვით თუ მუხტების რა სახის განაწილება გვაქვს. იმისათვის, რათა ვიპოვოთ «\(\dpi{120} \Sigma\) ზედაპირით შემოფარგლულ \(\dpi{120} \Omega\) სივრცეში მოქცეული მუხტების ალგებრული ჯამი» უნდა გამოვიყენოთ ინტეგრების პროცედურა. მარჯვენა ნაწილში ჯამის ნაცვლად გაჩნდება შესაბამისი ინტეგრალი - წირითი, ზედაპირული ან მოცულობითი:

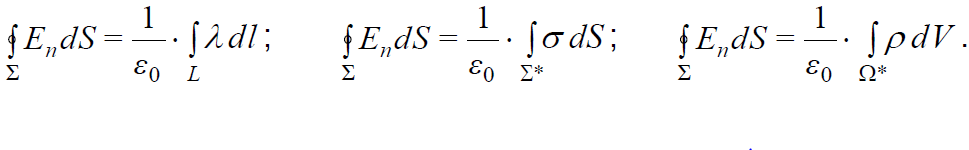
აქ \(\dpi{120} \lambda\), \(\dpi{120} \sigma\) და \(\dpi{120} \rho\) – ჩვენთვის უკვე ცნობილი მუხტის წრფივი, ზედაპირული და მოცულობითი სიმკვრივეებია შესაბამისად, ხოლო “L”, “\(\dpi{120} \Sigma\)*” და “\(\dpi{120} \Omega\)” – სხეულებია (სივრცის ნაწილები), რომელშიც არის მუხტი განაწილებული (ერთგანზომილებიანი, ორგანზომილებიანი და სამგანზომილებიანი).

2. კიდევ ერთხელ აღვნიშნოთ, რომ გაუსის თეორემა არის კულონის კანონისა და ძაბვის სუპერპოზიციის პრინციპის შედეგი.