სერიული პრეციზიული (ზუსტი) ექსპერიმენტების საფუძველზე ფრანგმა ფიზიკოსმა შარლ კულონმა 1785 წელს ჩამოაყალიბა ელექტროსტატიკის ძირითადი კანონი
ორ უძრავ წერტილოვან მუხტს შორის ურთიერთქმედების ძალა ვაკუუმში პირდაპირპროპორციულია ამ მუხტების მოდულების ნამრავლის და უკუპროპორციულია მათ შორის მანძილის კვადრატის. ეს ძალა არის მიზიდვის თუ მუხტები საპირისპირო ნიშნებისაა და - განზიდვის თუ ისინი ერთნიშნაა. ძალა მიმართულია მუხტების შემაერთებელი წრფის გასწვრივ.
მათემატიკურად კულონის კანონი ასე შეიძლება ჩავწეროთ
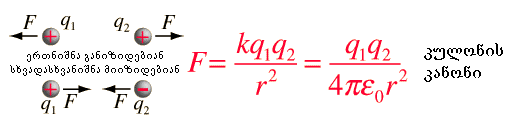 (15.1)
(15.1)
სადაც ε0 არის დიელექტრიკული შეღწევადობა. შევნიშნოთ, რომ ეს აკმაყოფილებს ნიუტონის მესამე კანონს, რადგან გულისხმობს, რომ q2 მუხტზე მოდულით ტოლი და მიმართულებით საპირისპირო ძალა მოქმედებს, რაც q1 მუხტზე. შევნიშნოთ, რომ კულონის კანონი იგივე ფორმისაა რაც გრავიტაციის კანონი.
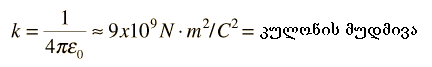
არის კულონის მუდმივა.
►აქვე მცირე შენიშვნები
- რამდენად ზუსტია კულონის კანონში 1/r2 დამოკიდებულება? არის თუ არა ხარისხის მაჩვენებელი ზუსტად 2-ის ტოლი? დღესდღეობით ექსპერიმენტული შემოწმებები აჩვენებს, რომ სიზუსტე დაცულია. სულ მცირე მძიმის შემდეგ 9 ნიშნის სიზუსტით მაინც.
- კულონის კანონით აღწერილი ძალა მოქმედებს ასევე მოძრავ მუხტებს შორის, მაგრამ აქ ეს ძალა არ არის სრულად ელექტრული (არამედ არის ელექტრომაგნიტური) ძალა. წარმოიქმნება შესწორება - მაგნიტური მდგენელი, რაც სწორედ სხეულის მოძრაობასთან არის დაკავშირებული. ამას მოგვიანებით განვიხილავთ.
ელექტრომაგნიტური ურთიერთქმედებების დროს თავს იჩენს ზოგიერთი ელემენტარული ნაწილაკის განსაკუთრებული თვისება - ელექტრული მუხტი. რას წარმოადგენს ელექტრული მუხტი? სამწუხაროდ ჭეშმარიტი პასუხის გაცემა ალბათ შეუძლებელია. ამიტომ შემოვიფარგლებით მხოლოდ იმის თქმით, რომ ეს არის ნაწილაკებისა და სხეულების ელექტრული და მაგნიტური ურთიერთქმედების უნარის საზომი. კულონი მუხტს უწოდებდა სხეულის „ელექტრულ მასას“.
აქვე მოვიყვანოთ ელექტრული მუხტის ძირითადი თვისებები.
1. არსებობს „დადებითი“ და „უარყოფითი“ მუხტები. მათ შორის არ არსებობს რაიმე ფუნდამენტური განსხვავება - ანუ სამყაროში არაფერი შეიცვლებოდა თუ შევცვლიდით „-“ ნიშანს „+“ ნიშნით.
2. ელექტრული მუხტი არის ზოგი ნაწილაკის განუყოფელი თვისება! ელექტრული მუხტის მინიმური წილი (|e| \(\cong\)1,6×10-19 კლ) ერთნაირია უარყოფითი და დადებითი ელექტრობისთვის - ამ ტოლობის ფარდობითი სიზუსტე არ არის უარესი 10-20-ზე! მაკროსკოპული სხეულების მუხტი q არის ადიტიური სიდიდე და იცვლება დისკრეტულად, ანუ ყოველთვის სრულდება q = ±N·|e|.
3. ელექტრული მუხტი ემორჩილება კიდევ ერთ ფუნდამენტურ კანონს - ელექტრული მუხტის შენახვის კანონს:
ელექტრულად იზოლირებულ სისტემაში ელექტრული მუხტების ალგებრული ჯამი არ იცვლება დროის განმავლობაში (\(\sum q_{i}=const\)).
ელექტრულად იზოლირებული ეწოდება სისტემას რომელსაც არ ტოვებენ და რომელშიც გარედან არ აღწევენ დამუხტული სხეულები ან ნაწილაკები.
4. ელექტრული მუხტი ათვლის სისტემის არჩევის მიმართ არის ინვარიანტული (ანუ არ არის მასზე დამოკიდებული). ამას გარდა, ის არ არის დამუხტული ნაწილაკის მოძრაობის მდგომარეობაზე.
ელექტროდიმნამიკა არის ფიზიკის ნაწილი, რომელიც სწავლობს დამუხტული სხეულების ურთიერთქმედებას და ელექტრული და მაგნიტური ველების თვისებებს.
მექანიკაში განიხილებოდა მხოლოდ ერთადერთი ფუნდამენტური ურთიერთქმედების კანონი - მსოფლიო მიზიდულობის კანონი. ყველა დანარჩენი ძალები, რომლებიც გვხვდებოდა მექანიკაში არის სხვა ფუნდამენტური ურთიერთქმედების გამოვლინება. ეს არის ელექტრომაგნიტური ურთიერთქმედება, რომელსაც შევისწავლით სწორედ ფიზიკის ამ ნაწილში.
დავიწყებთ სხეულის ელექტრული თვისებების გამოვლინების ყველაზე მარტივი შემთხვევით - ელექტროსტატიკით (უძრავი ელექტრულად დამუხტული სხეულები).
ამოცანის პირობიდან: \(V=\frac{\alpha }{T}\) და \(\nu =1\)
ვიცით, რომ \(\Delta Q= \Delta A+\Delta U\) (*)
ვიპოვოთ მუსაობა \(\Delta A=\int PdV\) (1)
რადგან \(V=\frac{\alpha }{T}\),
ამიტომ \(dV=-\frac{\alpha }{T^{2}}dT\) (2),
ხოლო მდგომარეობის განტოლებიდან ვიცით \(P=\frac{RT}{V}=\frac{RT^{2}}{\alpha }\) (3)
ჩავსვათ (2) და (3) გამოსახულება (1)-ში, მივირებთ:
\(\Delta A=-R\Delta T\) (4)
შინაგანი ენერგიის ცვლილება \(\Delta U=c_{V}\Delta T=\frac{R}{\gamma -1}\Delta T\) (5)
ჩავსვათ (5) და (4) გამოსახულება (*)-ში, გვექნება
\(\Delta Q=R\Delta T\frac{2-\gamma }{\gamma -1}\)


