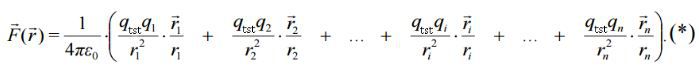კულონის კანონისა და სუპერპოზიციის პრინციპის გამოყენებით ელექტრული ველის დაძაბულობის გათვლა მუხტების მოცემული განაწილებისთვის პრინციპულად ყოველთვის არის შესაძლებელი. სხვა საქმეა, რომ ზუსტი ანალიზური შედეგის მიღება რიცხვითი მეთოდების გამოუყენებლად შესაძლებელია მხოლოდ წყარო მუხტების სივრცეში განაწილების შემთხვევათა ძლიერ შეზღუდული რაოდენობისთვის.

მოვიყვანოთ ასეთი გათვლის უმარტივეს შემთხვევა.

მაგალითი. განვსაზღვროთ R  რადიუსის მქონე თანაბრად დამუხტული რგოლის ელექტრული ველის  დაძაბულობა  რგოლის ღერძზე. წრის მუხტია q,  x  არის წრის ცენტრიდან დაშორება. 

დავყოთ რგოლი შემადგენელ ელემენტებად - წერტილოვან მუხტებად \(\dpi{120} \Delta q_{i}\), რომელთაგან თითოეული ქმნის А  წერტილში ველს შემდეგი დაძაბულობით

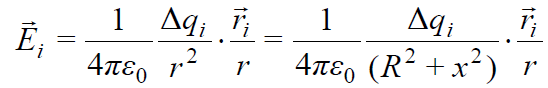
დაშორება რგოლის ელემენტიდან А წერტილამდე ყველა ელემენტისთვის ერთნაირია. ყველა ვექტორი ერთნაირი \(\alpha\)  კუთხით არის დახრილი ОХ ღერძის მიმართ. გამოვიყენოთ სუპერპოზიციის პრინციპი და შევკრიბოთ ყველა ეს ვექტორი. ამოცანის სიმეტრიის საფუძველზე საერთო მდგენელში წვლილი შეაქვთ მხოლოდ ღერძზე მდგენელებს

ამიტომ А წერტილში დაძაბულობის მოდული მხოლოდ ამ მდგენელების ჯამის ტოლი იქნება:

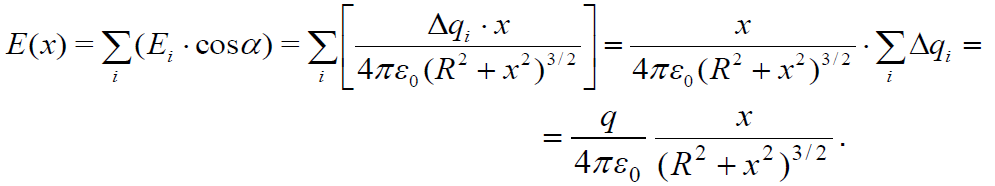
თვით დაძაბულობის ვექტორი კი ცხადია მიმართული იქნება  ОХ  ღერძის გასწვრივ. საბოლოოდ მიღებული შედეგი ასე ჩაიწერება:

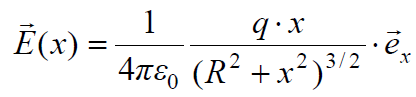                   (15.6)

 

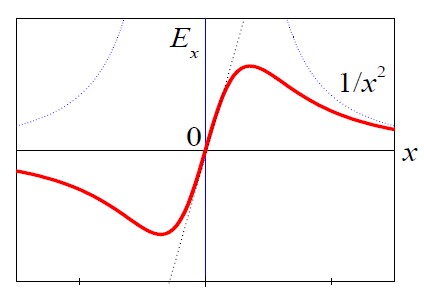
ნახაზზე მოყვანილია დაძაბულობის ვექტორის ОХ ღერძზე მდგენელის Ex დამოკიდებულება x-ზე. ჩანს, რომ რგოლის ცენტრიდან მცირე მანძილებზე  ეს დამოკიდებულება წრფივია, დიდ მანძილებზე კი მანძილის კვადრატის უკუპროპორციულია (რგოლი „გადაიქცევა“ წერტილოვან მუხტად).

►​ აქვე რამდენიმე შენიშვნა

1. განხილულ ამოცანას თავი გავართვით უმაღლესი მათემატიკის გარეშეც კი, ანუ ინტეგრირების პროცედურის გარეშე. მუხტების „ერთგანზომილებიანი“ განაწილების უფრო რთულ შემთხვევებში აუცილებელი ხდება ე.წ. „მრუდწირული“ ინტეგრალების გამოთვლა «L» წირითი ობიექტის გასწვრივ (მაგალითად ძაფი, მავთული და სხვ.):

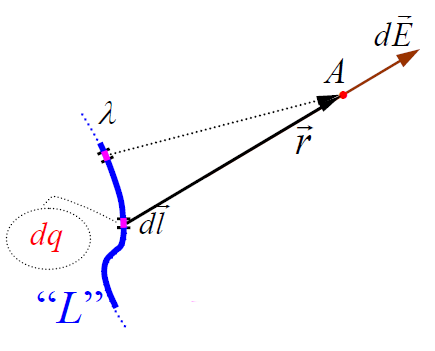
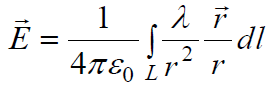                           (15.7)

ამ შემთხვევაში ვიყენებთ მუხტის წრფივი სიმკვრივის  ცნებას:

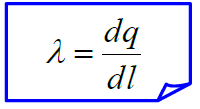                              (15.8)

ამ ტოლობის დაწერა რთული არ არის, მაგრამ აი ასეთი ინტეგრალის ამოღება, სამწუხაროდ, ყოველთვის არ არის შესაძლებელი.

2. თუ მუხტი განაწილებულია რაიმე ზედაპირზე ან რაიმე სამგანზომილებიან მოცულობაში, მაშინ იყენებენ შესაბამისად ზედაპირულ ან მოცულობით ინტეგრალებს და ასევე მუხტის ზედაპირული სიმკვრივისა და მუხტის მოცულობითი სიმკვრივის ცნებებს:

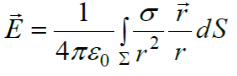   და 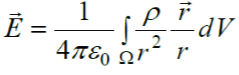 ​                            (15,9)

                                                         (15,10)

(15.9) და (15.9) ტოლობებში ინტეგრალქვეშა სიმბოლოები «L», «S» და «W» გამოიყენება იმ წირის, ზედაპირის და მოცულობის აღსანიშნავად, რომლებზედაც ხდება ინტეგრება.

თვალსაჩინოდ წარმოსახვისთვის შეიძლება ფურცელზე ყოველ წერტილში დავიტანოთ ელექტრული ველის დაძაბულობის ვექტორი და შემდეგ ეს ვექტორები შევაერთოთ წირით (ე.წ. ძალწირით) რაც გაკეთებულია ნახაზზე. 

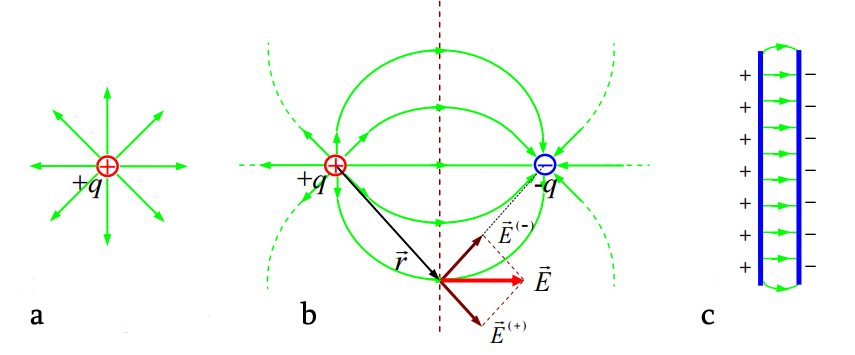
წირებს, რომლის ყოველ წერტილში მხებები ემთხვევა ელექტრული ველის დაძაბულობის ვექტორის მიმართულებას მოცემულ წერტილში, ეწოდებათ ელექტრული ველის დაძაბულობის წირები (ძალწირები).

ძალწირები გვეხმარება ელექტრული ველის სტრუქტურის აღსაქმელად მისი მიმართულებისა და სიდიდის შესაფასებლად. სიდიდეზე მსჯელობენ ძალწირების სიხშირით.

ნახაზზე მოყვანილია ერთეულოვანი წერტილოვანი მუხტის ელექტრული ველის ძალწირები, ბ)-ზე ორი ურთიერთსაპირისპირო მუხტის ელექტრული ველის ძალწირები და ც) ორი პარალელური დამუხტული ფირფიტის ველის ძალწირები. როგორც ბოლო ნახატზე ვხედავთ, პარალელურ ფირფიტებს შორის პარალელური წირებია. ასეთ ველს ერთგვაროვან ველს უწოდებენ. ელექტრულ ველს ეწოდება ერთგვაროვანი, თუ მისი დაძაბულობა სივრცის ნებისმიერ წერტილში ერთნაირია. ერთგვაროვანი ველის ძალწირები თანაბრად დაშორებულია ერთმანეთისგან და ურთიერთპარალელურია.

►აქვე გავაკეთოთ მნიშვნელოვანი შენიშვნები ელექტრული ველის ძალწირებზე

1. ელექტრული ველის ძალწირები არ არის ჩაკეტილი! ესეთი ველი წარმოშობილია წყაროებით - ელექტრული მუხტებით - მისი ძალწირები იწყება დადებითი მუხტებიდან და ბოლოვდება უარყოფით მუხტებზე.
2. დაძაბულობის წირები არ გადაიკვეთება.
3. როგორც უკვე აღვნიშნეთ ძალწირების სიხშირე მიუთითებს დაძაბულობის სიდიდეზე. წერტილოვანი მუხტის შემთხვევაში ძალწირები არა მარტო სტრუქტურულად სწორედ აღწერს ველს არამედ რაოდენობრივადაც ზუსტად აფასებს დაძაბულობის სიდიდის კლებას მუხტიდან დისტანციაზე, ძალწირები ერთმანეთს შორდება და მათი სიხშირე მანძილის კვადრატის უკუპროპორციულია. 

    

​

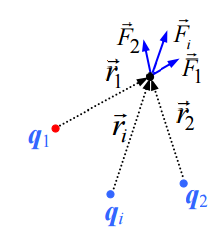
უნდა აღინიშნოს, რომ ელექტროსტატიკური ურთიერთქმედების კანონის ფორმულირება მოიცემა „წერტილოვანი“ სხეულებისთვის. ცდა აჩვენებს, რომ ელექტროსტატიკური ურთიერთქმედების ძალებისთვის სამართლიანია სუპერპოზიციის პრინციპი. ყოველი ელექტრული ზემოქმედება წერტილოვან მუხტზე (დავარქვათ მას საცდელი მუხტი) მუხტების ჯგუფიდან თითოეული მუხტის მხრიდან აღიწერება ძალით - ვექტორული სიდიდით, რომელიც შეიძლება მოიძებნოს კულონის კანონით. მთელი n მუხტისგან შედგენილი ჯგუფის ელექტრული ზემოქმედება ყველა  ძალის ვექტორული ჯამის ტოლია

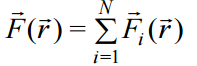             (15.2)

ეს ელექტროსტატიკური ძალების მნიშვნელოვანი თვისება არის. ორი მუხტის ურთიერთქმედების ძალა არ იცვლება მესამე, მეოთხე და ა.შ. მუხტების არსებობით.

ახლა ელექტრული ველის, როგორც სხეულების ელექტრულ ურთიერთქმედებაში შუამავლის კონცეფციაზე დაყრდნობით შემოვიტანოთ ელექტრული ველის მნიშვნელოვანი მახასიათებელი - ელექტრული ველის დაძაბულობა.

ელექტრული ველის დაძაბულობა ეწოდება ველის მოცემულ წერტილში მოთავსებულ საცდელ (წერტილოვან) მუხტზე მოქმედი ძალის ფარდობას ამ საცდელი მუხტის სიდიდესთან.

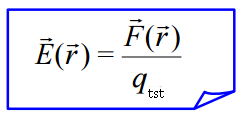                     (15.3)

აქ 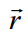არის ათვლის მოცემულ სისტემაში წერტილის მდებარეობის მახასიათებელი რადიუს-ვექტორი.

ახლა ავხსნათ, თუ რატომ დაგვჭირდა საცდელი მუხტის სიდიდეზე გაყოფა. წარმოვიდგინოთ, რომ საცდელი მუხტი მოთავსებულია სხვა წერტილოვანი მუხტების ველში. მასზე კულონის კანონით და სუპერპოზიციის პრინციპის გათვალისწინებით მოქმედებს ძალა

ჩანს, რომ სისტემის ყველა შესაკრებს აქვს თანამამრავლი \(\dpi{120} q_{tst}\). ამიტომ ტოლქმედი ძალა პროპორციულია \(\dpi{120} q_{tst}\)-ის. ახლა კი ნათელია, რომ ამ ძალის \(\dpi{120} q_{tst}\)-ზე გაყოფით მივიღებთ სიდიდეს, რომელიც არ არის საცდელი მუხტის სიდიდეზე (და საერთოდ მის არსებობაზე) დამოკიდებული ანუ ახასიათებს თვით მუხტების სისტემის ძალების ველს. სწორედ ეს არის დაძაბულობა .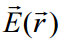

ასე რომ, ფუნქცია 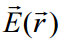 ახასიათებს სივრცის ყოველ წერტილს. თუ მოცემულია ასეთი ფუნქცია 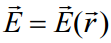, ამბობენ, რომ „მოცემულია ველი“. არსებითად, სწორედ ვექტორული ფუნქცია 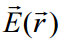არის ელექტრულ ველი. რატომ არის ასეთი მახასიათებლის შემოღება მოსახერხებელი? თუ რამენაირად ვისწავლით მუხტების მოცემული განაწილებით (თეორიულად ან ექსპერიმენტულად) ვიპოვოთ ელექტრული ველის დამოკიდებულებას კოორდინატზე - 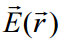, შევძლებთ ვიპოვოთ ძალა, რომელიც მოქმედებს ნებისმიერ საცდელ q მუხტზე, რომელიც მოთავსებულია მოცემულ წერტილში:

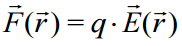                            (15.4)

წერტილოვანი მუხტის ველის დაძაბულობა

კულონის კანონიდან და ელექტრული ველის დაძაბულობის განსაზღვრებიდან მარტივად მიიღება ერთეულოვანი მუხტის ელექტრული ველის დაძაბულობა

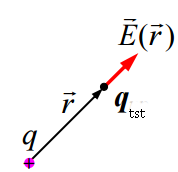
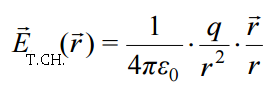                         .                                   (15.5)

გადავწეროთ (*) ტოლობა ასე:

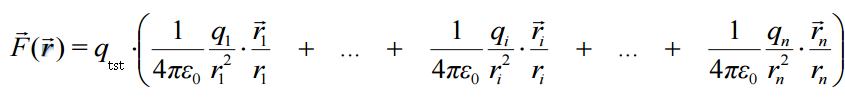
ანუ ​  ,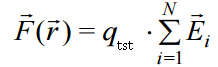

მაშინ (15.4)-ის გათვალისწინებით შედეგად მივიღებთ ელექტრული ველის დაძაბულობის  სუპერპოზიციის პრინციპს.

იმისათვის, რათა მივიღოთ განფენილი დამუხტული სხეულის ელექტრული ველის დაძაბულობა, აუცილებელია დავყოთ ის მცირე ელემენტებად (წერტილოვანი მუხტებად), ხოლო შემდეგ გამოვიყენოთ სუპერპოზიციის პრინციპი. მაგალითად ასეთი მეთოდით შეიძლება ვიპოვოთ დამუხტული სფეროს ელექტრული ველის დაძაბულობა. სფეროს გარეთ მისი ელექტრული ველის დაძაბულობა ისეთივეა, როგორც წერტილოვანი მუხტისა, რომელიც მოთავსებულია სფეროს ცენტრში, ხოლო სფეროს შიგნით დაძაბულობა ნულის ტოლია. 

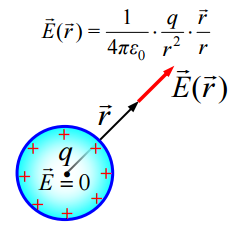
მიუხედავად მარტივი გეომეტრიისა ამის დამტკიცება საკმაოდ ჩახლართული მათემატიკური ამოცანაა და მოგვიანებით ვაჩვენებთ, თუ როგორ შეიძლება გაუსის ინტეგრალური თეორემის გამოყენებით გაცილებით იოლად დავასაბუთოთ ეს.

♦აქვე რამდენიმე შენიშვნა.

1, საცდელი მუხტი უნდა იყოს წერტილოვანი, ანუ დამუხტული სხეულის გეომეტრიული ზომები უნდა იყოს მცირე. მაგრამ რასთან შედარებით. სამწუხაროდ ამის დადგენა მხოლოდ ექსპერიმენტულად არის შესაძლებელი. საცდელი მუხტის ზომების შემცირებით შედეგი არ უნდა იყოს დამოკიდებული მისი ზომების შემდგომ შემცირებაზე.

2, საცდელი მუხტი სიდიდით უნდა იყოს მცირე. რა არის ამ სიმცირის კრიტერიუმი? ელექტრული ველის დაძაბულობის გასაზომად საცდელი ელექტრული მუხტის გაჩენამ არ უნდა შეცვალოს ამ ველის შემქმნელი მუხტების განაწილება. საკითხი აქაც უფრო ხშირად წყდება ექსპერიმენტულად.