მარტივად საჩვენებელია, რომ qi მუხტების სისტემის ველის პოტენციალისთვის სამართლიანია სუპერპოზიციის პრინციპი: ის ცალკეული მუხტის მიერ მოცემულ წერტილში შექმნილი პოტენციალის ალგებრული ჯამის ტოლია:
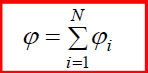 (17.9)
(17.9)
ამ დებულების დამტკიცება ემყარება ორ ჩვენთვის ცნობილ გარემოებას: 1) პოტენციალი საცდელი მუხტის მოცემული წერტილიდან ნორმირების წერტილში გადატანაზე შესასრულებელი კუთრი მუშაობის ტოლია; 2) ძალის მუშაობა არის ადიტიური სიდიდე, ანუ სხეულზე მოქმედი რამდენიმე ძალის მუშაობა ყოველთვის ტოლია ცალკეული ძალის ამ სხეულზე მოქმედებით შესრულებული მუშაობების ალგებრული ჯამისა.
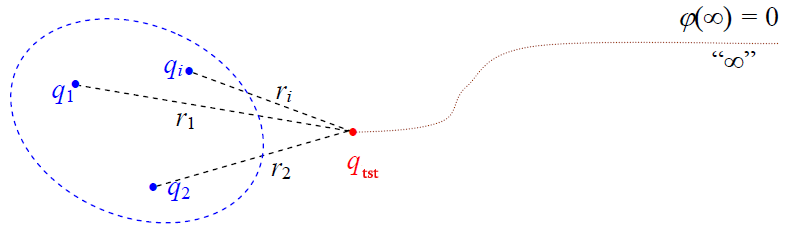
წერტილოვანი მუხტების სისტემის ველისთვის, შესაბამისად, შეიძლება
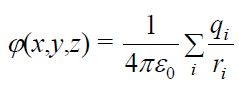 (17.10)
(17.10)
სადაც ri – არის i-ური მუხტისგან დაშორება {x,y,z}კოორდინატების მქონე ველის წერტილამდე. მოვიყვანოთ განვრცობილი დამუხტული სხეულის მიერ შექმნილი ველის პოტენციალის გამოთვლის მარტივი მაგალითი, რომელიც ემყარება პოტენციალთა სუპერპოზიციის პრინციპს.
მაგალითი. განვსაზღვროთ თანაბრად დამუხტული R რადიუსის მქონე რგოლის მიერ შექმნილი ველის φ(x) პოტენციალი ამ რგოლის ღერძზე. რგოლის მუხტია q, x – არის რგოლის ცენტრიდან დაშორება.
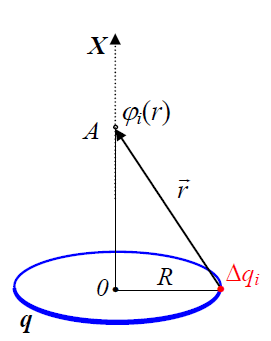
პოტენციალი არის სკალარული სიდიდე და რგოლის აზრობრივად Δqi მუხტის მქონე ელემენტებად დაყოფის შემდეგ, სუპერპოზიციის პრინციპის შესაბამისად უნდა შევკრიბოთ სრულიად ერთნაირი სიდიდეები - ველის პოტენციალები, რომლებსაც ჩვენთვის საინტერესო წერტილში ქმნიან რგოლის ცალკეული ელემენტები:
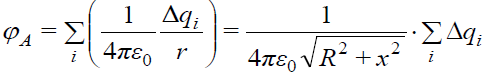
დარჩენილი ჯამი გვაძლევს, რა თქმა უნდა, რგოლის სრულ q მუხტს. ამიტომ შედეგი საბოლოოდ ასე ჩავწეროთ:
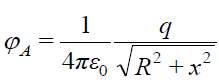 (17.11)
(17.11)
ეს შედეგი მათემატიკური თვალსაზრისით ძალიან მარტივად მივიღეთ სწორედ პოტენციალის სკალარული ხასიათის გამო.
ველისა და პოტენციალის ენერგეტიკული დახასიათებისთვის შემოიღეს დამატებითი (ძალწირებთან ერთად) საილუსტრაციო მახასიათებელი - ექვიპოტენციურ ზედაპირთა სისტემა. დასახელებიდანვეა ნათელი (ექვი - ნიშნავს ტოლს), რომ ეს არის მუდმივი პოტენციალის მქონე ზედაპირები. ამ ზედაპირების გასწვრივ რა თქმა უნდა მუშაობა საერთოდ არ სრულდება. მუშაობა მაქსიმალურია იმ მიმართულებით საითაც ექვიპოტენციური ზედაპირების სიმჭიდროვე არის მაქსიმალური. ამ ადგილებში მაქსიმალურია ველის დაძაბულობაც. ადვილია იმის მიხვედრა, რომ ძალწირებისა და ექვიპოტენციური ზედაპირების გადაკვეთის წერტილებში ისინი ურთიერთმართობებია. მართლაც ექვიპოტენციურ ზედაპირზე ნებისმიერი გადაადგილება არ იწვევს მუშაობის შესრულებას, ეს კი შესაძლებელია თუ გადაადგილების მყის ვექტორზე დაძაბულობის ვექტორის მდგენელი არის ნული, ანუ ველის ძალწირი არის მისი მართობი. ქვევით მოყვანილია ჩვენი მსჯელობის მათემატიკური ფორმალიზმი:
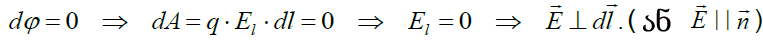
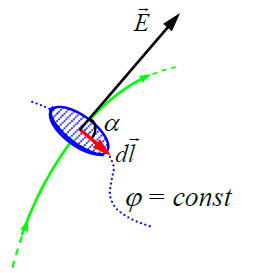 ნახაზთან ერთად ის ადასტურებს ჩვენს მიერ უკვე ჩამოყალიბებული მტკიცების არსს: დაძაბულობის ძალწირები კვეთენ ექვიპოტენციურ ზედაპირებს მართი კუთხით!
ნახაზთან ერთად ის ადასტურებს ჩვენს მიერ უკვე ჩამოყალიბებული მტკიცების არსს: დაძაბულობის ძალწირები კვეთენ ექვიპოტენციურ ზედაპირებს მართი კუთხით!
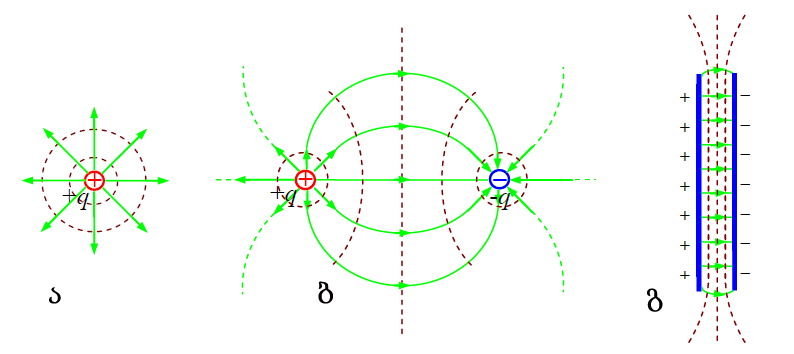
მოვიყვანოთ ექვიპოტენციური ზედაპირების ნახაზები ჩვენთვის უკვე ცნობილი ელექტრული ველებისთვის ა) წერტილოვანი მუხტის ველი; ბ) ორი მოდულით ტოლი და საპირისპირო მუხტის მქონე წერტილოვანი მუხტის ველი; გ) საპირისპირო მუხტის მქონე ორი ბრტყლად პარალელური დიდი (მათ შორის მანძილთან შედარებით) ფირფიტის ველი.
უკვე ვიცით რას უდრის წერტილოვანი მუხტის ნებისმიერ მუხტთა სისტემის ველთან ურთიერთქმედების პოტენციური ენერგია (იხ. ტოლობა 17.4):
U(x,y,z) = q•φ(x,y,z). (17.16)
ამიტომ q1 და q2 მუხტების კერძო შემთხვევაში მათი ურთიერთქმედების პოტენციური ენერგია არის:
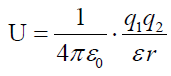 . (17.17)
. (17.17)
მოხერხებულია ეს განვიხილოთ, როგორც q2 მუხტის მეორე წყარო q1 მუხტის ელექტრულ ველთან ურთიერთქმედების პოტენციური ენერგია (ან პირიქით).
მივყვეთ პოტენციალის გამოთვლის პროცედურას და მივიღოთ წერტილოვანი მუხტის ველის პოტენციალის გამოსახულება. ამას დიდი მნიშვნელობა აქვს შემდგომში ნებისმიერად განაწილებული მუხტების სისტემის ველის პოტენციალის გამოსათვლელად.
1. ნორმირება. პოტენციალი ნულის ტოლად ჩავთვალოთ იქ სადაც წერტილოვანი მუხტის ველი პრაქტიკულად არ არის: 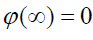 .
.
2. ტრაექტორიის არჩევა. ვთქვათ ნებისმიერი წერტილი  წყარო მუხტისგან იმყოფება r მანძილზე. რადგან შედეგი არ არის დამოკიდებული ტრაექტორიაზე, (17.7) მრუდწირული ინტეგრალის გამოთვლისთვის ვირჩევთ უმარტივეს რადიალურად მიმართულ წრფეს მოცემული წერტილიდან ძალწირის გასწვრივ, რომელიც მიემართება უსასრულობაში.
წყარო მუხტისგან იმყოფება r მანძილზე. რადგან შედეგი არ არის დამოკიდებული ტრაექტორიაზე, (17.7) მრუდწირული ინტეგრალის გამოთვლისთვის ვირჩევთ უმარტივეს რადიალურად მიმართულ წრფეს მოცემული წერტილიდან ძალწირის გასწვრივ, რომელიც მიემართება უსასრულობაში.
3. გამოთვლა. (17.5) პოტენციალის განსაზღვრების შესაბამისად გამოვთვალოთ q წერტილოვანი მუხტის შექმნილი ველის მიერ საცდელი მუხტის არჩეულ ტრაექტორიაზე გადასატანად შესრულებული კუთრი მუშაობა. არჩეული ტრაექტორიის გამო მრუდწირული ინტეგრალი იცვლება ჩვეულებრივი განსაზღვრული ინტეგრალით:
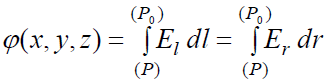
ახლა წერტილოვანი მუხტის ველის პროექციის ჩასმით (იხ. ტოლობა (15,5)) გვრჩება მხოლოდ მათემატიკური გარდაქმნები:
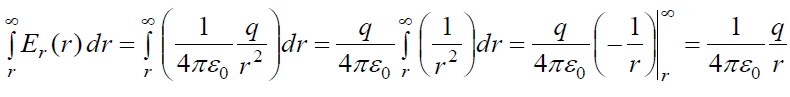 .
.
ცალკე ამოვწეროთ შესაძლო გარემომცველი აირის ან სითხის \(\varepsilon\) დიელექტრული შეღწევადობის გათვალისწინების დამატებით:
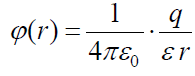 . (17.8)
. (17.8)
როგორც ვხედავთ წერტილოვანი მუხტის პოტენციალი r მანძილის უკუპროპორციულია.


