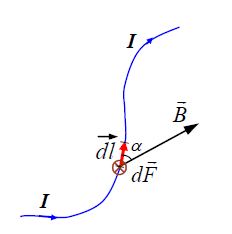
ვიცით, რომ მაგნიტური ველი მოქმედებს არა მარტო დენებზე, არამედ მოძრავ მუხტზეც. მაგნიტური ველის მოქმედების ამ ძალას უწოდებენ ლორენცის ძალას და იგი ტოლია
 მისი მოდული
მისი მოდული 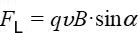
აქ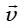
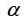
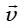
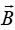
უკვე ვახსენეთ, რომ ამპერმა შესძლო ორ სწორ ურთიერთპარალელურ გრძელ მუდმივდენიან გამტარს შორის ურთიერთქმედების კანონის განსაზღვრა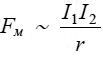
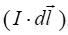
► მაგნიტურ ველში დენის ელემენტზე მოქმედი ძალა ტოლია
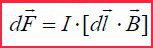
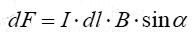
აქ 
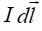
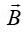
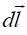
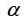
ამ ძალის მიმართულება განისაზღვრება "მარჯვენა ხელის" წესით. სასრულ გამტარზე მოქმედი სრული ძალა გამოითვლება, ჩვეულებრივ, "ელემენტური ურთიერთქმედებების" (ვექტორული) აჯამვით. კერძოდ ასეთნაირად შეიძლება გამოითვალოს ორი ურთიერთპარალელური სწორხაზოვანი დენიანი გამტარის ურთიერთქმედება. თითოეული გამტარის ერთეულოვან სიგრძეზე მოსული ძალა ამ შემთხვევაში ტოლია:
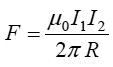
სადაც 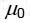
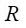
ა) ჯოულ-ლენცის კანონი ინტეგრალური ფორმით.
R წინაღობის მწონე წრედის 1-2 ერთგვაროვან უბანში ელექტრული დენის გავლისას ელექტრული ველი ასრულებს მუშაობას ამ გამტარში დენის მატარებელთა გადაადგილებაზე. ამ მუშაობას უწოდებენ "დენის მუშაობას". როგორც ვიცით ელექტროსტატიკიდან ელექტრული ველის მუშაობა ტოლია:


ენერგიის მუდმივობიდან გამომდინარე დენის მუშაობა ტოლია უბანზე ენერგიის ცვლილებისა. ის შეიძლება იხარჯებოდეს სითბოს გამოყოფაზე, ქიმიური რეაქციების მიმდინარეობაზე, გამოსხივებაზე, დენიანი გამტარის მოძრაობით მექანიკურ მუშაობის შესრულებაზე და ა.შ. თუ გამტარი უძრავია, ქიმიური რეაქციები არ მიდის და არ აქვს ადგილი სხვა სახის ენერგიის კარგვას, მაშინ დენის მთელი მუშაობა იხარჯება მასში სითბოს გამოყოფაზე 

► სითბოს რაოდენობა 

ჯოულ-ლენცის კანონი სრულდება არამარტო ლითონის გამტარებისთვის, არამედ ელექტროლიტებისა და აირებისთვისაც.
♦ შენიშვნა
ჯოულ-ლენცის კანონზე საუბრისას (20.2) თანაფარდობასთან ერთად უნდა მოვიყვანოთ ხშირად იყენებენ ასეთ თანაფარდობასაც 
ბ) ჯოულ-ლენცის კანონი დიფერენციული (ლოკალური) ფორმით.
ვნახოთ რა ხდება მიკროდონეზე (ანუ ლოკალურ დონეზე). გამოვიყენოთ იგივე ხერხი, რაც ომის კანონის ლოკალური ფორმით დასაბუთებისას – გამოვყოთ გამტარი გარემოს ფიზიკურად უსასრულოდ მცირე ელემენტი და ჩავწეროთ მისთვის მწკრივი საკმაოდ გასაგები ტოლობებისა:
თუ აქედან გამოვყოფთ სითბოგამოყოფის კუთრ სიმძლავრეს – ანუ სითბოს იმ რაოდენობას, რომელიც დროის ერთეულში გამტარი გარემოს მოცულობის ერთეულში გამოიყოფა, მაშინ ალგებრული გარდაქმნებით მივიღებთ სწორედ ჯოულ-ლენცის კანონს დიფერენციული ფორმით:


ამ თანაფარდობის ლოკალური ხასიათი ნიშნავს, რომ ყველა სიდიდე ტოლობის მარცხნივ და მარჯვნივ განეკუთვნება გამტარი გარემოს განსაზღვრულ წერტილს, უფრო ზუსტად ძალიან მცირე არეს, რომლის მდებარეობა მოიცემა 
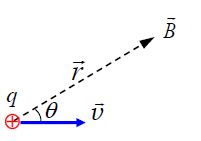
მოძრავი დამუხტული ნაწილაკი დენის ელემენტის ექვივალენტია და გარემომცველ სივრცეში ქმნის მაგნიტურ ველს. ამ ველის მაგნიტური ინდუქციის ვექტორის გამოსახულების მიღება რთული არ არის ბიო-სავარ-ლაპლასის კანონის გამოყენებით. ამისთვის გავიხსენოთ ჩვენთვის კარგად ცნობილი თანაფარდობები:
,
,

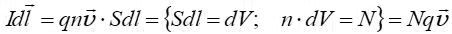
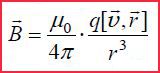
♦ შენიშვნა
ასეთია ნებისმიერი მოძრავი დამუხტული ნაწილაკის მიერ შექმნილი მაგნიტური ველი ელექტრული გამტარებლობის მეტალებში, ან ელექტრონულ-სხივურ მილაკებში ან ვაკუუმურ დიოდში, გინდაც იონის ელექტროლიტის ხსნარში მოძრაობისას, თუ მუხტის მოძრაობის სიჩქარე გაცილებით ნაკლებია სინათლის სხივის სიჩქარეზე. მაგნიტურ ველს ქმნიან მოძრავი დამუხტული სხეულებიც - მაკროსკოპული მუხტები.