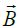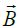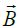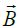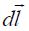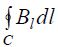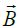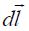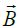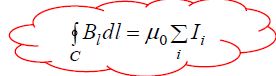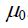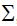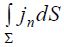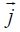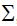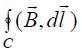მაგნიტური ველის ძალური მახასიათებლის,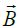 
მაგნიტური ველის ინდუქციის ვექტორის გამოყენება ნაყოფიერია თუ ჩვენ შეგვიძლია მისი გათვლა დენების (მოძრავი მუხტების) სივრცეში ცნობილი განაწილების მეშვეობით. ელექტროსტატიკის მსგავსად აქაც შეგვიძლია საუბარი ორ მეთოდზე. ერთი არის პირდაპირი და ეყრდნობა მაგნიტური ველის სუპერპოზიციის პრინციპის და ბიო-სავარ-ლაპლასის კანონის გამოყენებას. ჩვენ ეს მეთოდი ვაჩვენეთ უსასრულო სწორხაზოვანი გამტარის მაგნიტური ველის გათვლისას. პრინციპულად ეს მეთოდი გამოყენებადია ყოველთვის, მაგრამ ახლავს სერიოზული მათემატიკური სირთულეები.
ელექტროსტატიკის მსგავსად მაგნეტოსტატიკაში (ანუ უძრავი მუდმივდენიანი გამტარების შემთხვევაში) ვაყალიბებთ 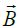ინდუქციის ვექტორის ცირკულაციის თეორემას. მისი გამოენება საშუალებას გვაძლევს მნიშვნელოვნად გაადვილდეს გამტარებში დენების მიერ შექმნილი მაგნიტური ველის პოვის ამოცანები მუხტის გადატანის ბრტყელი, ცილინდრული და სფერული სიმეტრიების დროს. ის წარმოადგენს სწორედ მაგნიტური ველის ინდუქციის ვექტორის მოძებნის "მეორე ხერხს". ის გამოიყენება დენების სივრცული განაწილების მხოლოდ ზოგიერთ კერძო ოღონდ საკმაოდ პრაქტიკულ და მნიშვნელოვან შემთხვევებში.
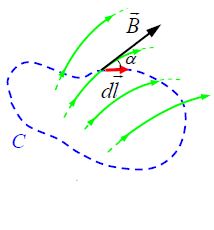
უწინარეს ყოვლისა შემოვიტანოთ თვით ვექტორული ველის ცირკულაციის ცნება მაგნიტოსტატიკური ველის მაგალითზე.. .
(განსაზღვრება) ვექტორის (მაგალითად 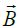) ცირკულაცია შეკრულ C კონტურზე ეწოდება შემდეგი სახის მრუდწირულ ინტეგრალს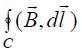 
ინტეგრების ნიშნის ქვეშ გვაქვს 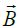და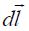 
ვექტორების სკალარული ნამრავლი და ის რა თქმა უნდა სკალარული სიდიდეა. მისი, ჩაწერა შეიძლება ასეთი ექვივალენტური ფორმით 
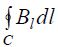, სადაც Bl არის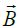ვექტორის მდგენელი კონტურის უსასრულოდ მცირე 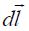ელემენტზე.
ახლა კი ჩამოვაყალიბოთ თეორემა.
მაგნიტოსტატიკური ველის ინდუქციის 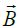ვექტორის ცირკულაცია ნებისმიერ შეკრულ C კონტურზე ვაკუუმში ამ კონტურით შემოფარგლულ ზედაპირში გამჭოლავი დენების ძალების ალგებრული ჯამის პროპორციულია:
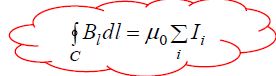( 23.1)
ერთეულთა SI სისტემაში პროპორციულობის კოეფიციენტი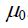 
მაგნიტური მუდმივის ტოლია. იმ შემთხვევაში, როცა C კონტურით შემოვარგლულ 
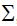ზედაპირში გადის განაწილებული დენები, ( 23.1) გამოსახულების მარჯვენა მხარეს ჯამის ნაცვლად ვწერთ ინტეგრალს 
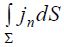. ეს ინტეგრალი წარმოადგენს 
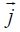ელექტრული დენის სიმკვრივის ვექტორის ნაკადს ზედაპირში.