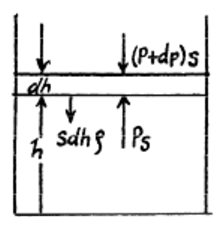
\(Sdh\rho g+\left ( p+dp \right )S=pS\), აქედან გვექნება,
\(dp=-\rho gdh\).
აირის მდგომარეობის განტოლებიდან ვიცით,
\(p=\frac{\rho }{M}RT\), ამიტომ მუდმივი ტემპერატურის დროს \(dp=\frac{d\rho }{M}RT\)
ასე რომ \(\frac{d\rho }{\rho }=\frac{gM}{RT}dh\)
შესაბამის საზღვრებში გაინტეგრებით
\(\int_{\rho _{0}}^{\rho }\frac{d\rho }{\rho }=\int_{0}^{h}\frac{gM}{RT}dh\)
ანუ
\(ln\frac{\rho _{0}}{\rho }=-\frac{gM}{RT}h\)
ასე რომ, \(\rho =\rho _{0}e^{-Mgh/RT}\) და \(h=-\frac{RT}{Mg}ln\frac{\rho }{\rho _{0}}\)
(ბ) მოცემულია \(T=273^{o}K\), \(\frac{\rho _{0}-\rho }{\rho_{0} }=0,01\) ანუ \(\frac{\rho }{\rho_{0} }=0,99\)
ამიტომ \(h=-\frac{RT}{Mg}ln\frac{\rho }{\rho _{0}}\)=0,09კმ