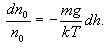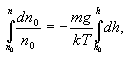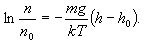თუ გავითვალისწინებთ, რომ Р=nkT, მაშინ (12.4)-ის გათვალისწინებით მივიღებთ შემდეგ განტოლებას
 |
(12.6) |
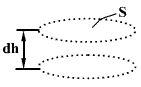
სადაც P0 - არის აირის წნევა h0 სიმაღლეზე. h0-ად ხშირად იღებენ ზღვის დონეს, ანუ თვლია h0=0 , მაშინ P0 წარმოადგენს ატმოსფერულ წნევას დედამიწის ზედაპირზე, Р - აირის წნევაა h სიმაღლეზე.
ამ გამოსახულებას ეწოდება ბარომეტრული ფორმულა. მიღებული განტოლებებიდან გამომდინარეობს, რომ როგორც მოლეკულების კონცენტრაცია ისე წნევა მცირდება ექსპონენციურად სიმაღლის ზრდით.
აირების კინეტიკური თეორიისა და მაქსველის განაწილების განხილვისას იგულისხმებოდა, რომ აირის მოლეკულებზე არ მოქმედებს არავითარი ძალა, მოლეკულების შეჯახებების გარდა. ამიტომ, მოლეკულები თაანაბრად ნაწილდება მთელს ჭურჭელში. სინამდვილეში ნებისმიერი აირის მოლეკულები ყოველთვის იმყოფება დედამიწის მიზიდულობის ველში. ამის შედეგად, ყოველი m მქონე მოლეკულა განიცდის სიმძიმის ძალის მოქმედებას f =mg.
გამოვყოთ აირის მოცულობის dh სიმაღლის S ფართის ფუძის მქონე ჰორიზონტული ელემენტი. ვთვლით, რომ აირი არის ერთგვაროვანი და მისი ტემპერატურა მუდმივი. ამ მოცულობაში მოლეკულების რიცხვი ტოლია მისი მოცულობის dV=Sdh ნამრავლისა მოლეკულების n0 რიცხვზე მოცულობის ერთეულში. გამოყოფილ ელემენტში მოლეკულების სრული წონა ტოლია
dF=n0Sdh·mg
dF წონის მოქმედება იწვევს წნევას, რომელიც ტოლია
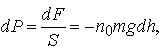 |
(12.2) |
მინუსი აქ იმიტომ არის, რომ dh-ის ზრდისას წნევა მცირდება. მოლეკულურ-კინეტიკური თეორიის ძირიტადი განტოლების თანახმად
| dP=kTdn0 | (12.3) |
(12.2)-ს და (12.3)-ის მარჯვენა მხარეების გატოლებით, მივიღებთ
kTdn0 = -n0mgdh
ანუ
გავაინტეგროთ ეს გამოსახულება საზღვრებში h0-დან h-მდე (შესაბამისად კონცენტრაცია იცვლება n0-დან n-მდე):
მივიღებთ
აქედან
 |
(12.4) |
exp-თან ხარისხის მაჩვენებელს აქვს მამრავლი mg(h-h0), რომელიც აირის მოლეკულის მოტენციური ენერგიის ნაზრდს განსაზღვრავს. თუ მოლეკულას გადავანაცვლებთ h0 დონიდან h დონეზე, მაშინ მისი პოტენციური ენერგიის ცვლილება იქნება
ΔW = mgh-mgh0
მოლეკულების კონცენტრაციის განტოლება მიიღებს სახეს
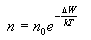 |
(12.5) |
ეს განტოლება გამოსახავს ბოლცმაბის ზოგად კანონს და იძლევა ნაწილაკების რიცხვის განაწილებას მათი პოტენციური ენერგიის მიხედვით. ის გამოიყენება ნაწილაკების ნებისმიერი სისტემისთვის, რომელიც ძალურ ველში იმყოფება, მაგალითად ელექტრულში.
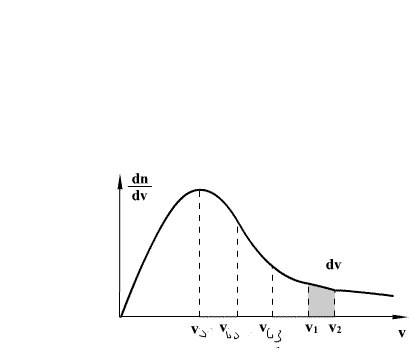
აირის მოლეკულების სიჩქარეებს აქვთ განსხვავებული მნიშვნელობები და მიმართულებები, ამასთან დაჯახებების უზარმაზარი რიცხვის გამო, თითოეული მოლეკულის სიჩქარე მუდმივად იცვლება. ამიტომ შეუძლებელია განისაზღვროს ზუსტად იმ მოლეკულების რიცხვი, რომელთაც აქვთ ზუსტად მოცემული სიჩქარე v დროის მოცემულ მომენტში, მაგრამ შეიძლება გამოითვალოს იმ მოლეკულების რიცხვი, რომელთა სიჩქარეებს აქვთ მნიშვნელობები, რომლებიც ძევს რაღაც v1 და v2 სიჩქარეებს შორის.
გამოვიყვანოთ სითბურ წონასწორობაში მყოფი ნაწილაკების სიჩქარეების განაწილება. თერმულ წონასწორობაში შეგვიძლია გამოვიყენოთ მაქსველ-ბოლცმანის სტატისტიკა, სადაც T ტემპერატურაზე ენერგეტიკული მდგომარეობის ალბათობა მოიცემა ფორმულით
\(P\left ( \epsilon _{i} \right )=\frac{exp\left ( -\epsilon _{i} \right /kT)}{\sum _{j}exp\left ( -\epsilon _{j} \right /kT)}\)
გამყოფი არის მანორმალიზებელი კოეფიციენტი, რომელიც გამოითვლება ყველა შესაძლო ენერგეტიკული მდგომარეობის აჯამვით. იდეალური აირისთვის შინაგან ენერგიას ვიცით განსაზღვრავს კინეტიკური ენერგია და ამიტომ ზოგადად სიჩქარის განაწილების ფუნქცია შეგვიძლია ჩავწეროთ ასე
\(f\left ( \vec{v} \right )=Cexp\left ( -\frac{m\left |\vec{v} \right |^{2}}{2kT} \right )=Cexp\left ( -\frac{m\left ( v_{x}^{2}+v_{y}^{2}+v_{z}^{2} \right )}{2kT} \right )\)
ანუ ეს არის ალბათობა იმისა, რომ ნაწილაკს აქვს \(\vec{v}\) სიჩქარე. ყველა შესაძლო სიჩქარეებით აჯამული ალბათობა ცხადია იქნება 1-ის ტოლი. ამიტომ C ნორმირების ფაქტორისთვის გვექნება
\(1/C=\sum _{i}exp\left ( -\frac{m\vec{v_{i}}^{2}}{2kT} \right )\)
რადგან სიჩქარების მნიშვნელობები არის უწყვეტი, ჯამი გადადის ინტეგრალში და რადგან სიჩქარეს აქვს სამი განზომილება, ამიტომ ინტეგრება უნდა მოვახდინოთ სამივე კოორდინატით
\(1/C=\int_{-\infty }^{\infty}\int_{-\infty }^{\infty}\int_{-\infty }^{\infty}exp\left ( -\frac{m\left ( v_{x}^{2}+v_{y}^{2}+v_{z}^{2} \right )}{2kT} \right )dv_{x}dv_{y}dv_{z}\)
შეგვიძლია დავყოთ სამ გაუსის ინტეგრალად
\(1/C=\int_{-\infty }^{\infty}exp\left ( -\frac{m\left ( v_{x}^{2} \right )}{2kT} \right )dv_{x}\int_{-\infty }^{\infty}exp\left ( -\frac{m\left ( v_{y}^{2} \right )}{2kT} \right )dv_{y}\int_{-\infty }^{\infty}exp\left ( -\frac{m\left ( v_{z}^{2} \right )}{2kT} \right )dv_{z}\)
გაუსიანების ინტეგრებით მივიღებთ
\(1/C=\left ( \frac{2\pi kT}{m} \right )^{3/2}\)
საბოლოოდ განაწილების ფუნქცია გვექნება ამ სახით:
\(f\left ( \vec{v} \right )=\left ( \frac{m}{2\pi kT} \right )^{3/2}exp\left ( -\frac{mv^{2}}{2kT} \right )\)
სადაც \(v=\left | \vec{v} \right |=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}\)
ასე რომ, მივიღეთ სიჩქარის ვექტორის განაწილების ფუნქციის გამოსახულება. მაგრამ გაცილებით მოხერხებულია და ხშირად იხმარება სიჩქარის განაწილება და არა სიჩქარის ვექტორის. მოცემულ \(v\)-ზე მისი კომპონენტების ნებისმიერი კომბინაცია რომელიც აკმაყოფილებს \(v^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\) გამოსახულებას, იქნება ვარგისი. ანუ ეს იმის ანალოგიურია, რომ ვიპოვოთ იმ სფეროს ყველა წერტილი (ანუ ფართობი) რომლის რადიუსი შეესაბამება \(v\)-ს ანუ ამ სფეროზე გვექნება \(4\pi v^{2}\) მდგომარეობა ნებისმიერი მოცემული \(v\)-თვის. ამდაგვარად შეგვიძლია მაქსველის სიჩქარის ვექტორის განაწილების ფუნქცია გარდავქმნათ მაქსველის სიჩქარის განაწილების ფუნქციად ასე
| \(f\left (v \right )=4\pi\left ( \frac{m}{2\pi kT} \right )^{3/2}v^{2}exp\left ( -\frac{mv^{2}}{2kT} \right )\) | (12.1) |
თერმულ წონასწორობაში შეგვიძლია შევაფასოთ სისტემის მახასიათებელი სიჩქარეები. ერთერთი ასეთი სიჩქარე არის ყველაზე ალბათური სიჩქარე, ანუ სიჩქარეზე, რომელთანაც ახლოს არის უმეტესობა მოლეკულების სიჩქარეები. ყველაზე ალბათური სიჩქარე შეესაბამება განაწილების ფუნქციის მაქსიმალურ მნიშვნელობას. ანუ როცა
\(\frac{\mathrm{d} f\left (v \right )}{\mathrm{d} v}=0\)
აქედან მარტივი გარდაქმნებით მივიღებთ
\(v_{p}=\sqrt{2kT/m}\)
შემდეგი სიჩქარე, რომელსაც ვიპოვით არის არის საშუალო სიჩქარე \(v_{m}\). სიჩქარის განაწილების ფუნქციის გამოყენებით საშუალო სიჩქარის გამოსათვლელად ვიყენებთ შემდეგ გამოსახულებას
\(v_{m}=\int_{0}^{\infty }f\left ( v \right )vdv\)
გარდაქმნებით მივიღებთ,
\(v_{m}=\sqrt{\frac{8kT }{\pi m}}\)
ჩანს, რომ საშუალო სიჩქარე ოდნავ მეტია ყველაზე ალბათურ სიჩქარეზე რადგან (\(\sqrt{\frac{8 }{\pi }}> \sqrt{2}\)). ბოლო სიჩქარე, რომელსაც ვიპოვით არის საშუალო კვადრატული სიჩქარე \(v_{rms}\). განვსაზღვროთ საშუალო კვადრატული სიჩქარე ასე \(v_{rms}^{2}\equiv \bar{v^{2}}\). \(\bar{v^{2}}\) -ის საპოვნელად ვწერთ
\(\bar{v_{2}}=\int_{0}^{\infty }f\left ( v \right )v^{2}dv\)
გარდაქმნებით მივიღებთ
\(v_{rms}=\sqrt{\frac{3kT }{m}}\)
dV-ს ქვეშ დაშტრიხული ზოლის ფართობი აჩვენებს მოლეკულების საერთო რაოდენობიდან რა ნაწილს აქვს სიჩქარეები ამ ინტერვალში. მაქსველის განაწილების ფუნქციის კონკრეტული სახე დამოკიდებულია აირის გვარობაზე (მოლეკულის მასაზე) და ტემპერატურაზე. აირის წნევა და მოცულობა მოლეკულების სიჩქარეების განაწილებაზე არ მოპქმედებს.
ტემპერატურის გაზრდით ყველაზე ალბათური სიჩქარე იზრდება, ამიტომ მოლეკულების სიჩქარეების მიხედვით განაწილების მაქსიმუმი წაინაცვლებს მაღალი ისჩქარეებისკენ. შესაბამისად, აირის გათბობისას იმ მოლეკულების წილი, რომლებსაც აქვთ მცირე სიჩქარეები მცირდება, ხოლო მაღალი სიჩქარეების მქონე მოლეკულების წილი იზრდება.
იდეალური აირის თეორიაში მოლეკულების ურთიერთქმედების პოტენციური ენერგია ითვლება ნულის ტოლად. ამიტომ იდეალური აირის შინაგანი ენერგია განისაზღვრება ყველა მისი მოლეკულის მოძრაობის კინეტიკური ენერგიით. ერთი მოლეკულის მოძრაობის საშუალო ენერგია ტოლია
რადგან ერთ მოლში არის 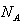
\(U_{0}=\bar{W}_{k}N_{A}=\frac{i}{2}N_{A}kT\)
ვითვალისწინებთ რა, რომ 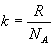
\(U_{0}=\frac{i}{2}RT\)
აირის ნებისმიერი m მასისითვის, ანუ მოლების ნებისმიერი რიცხვისთვის 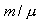
| \(U=\frac{im}{2\mu }RT\) | (11.12) |
ამ გამოსახულებიდან გამომდინარეობს, რომ U არის მდგომარეობის ცალსახა ფუნქცია და შესაბამისად, სისტემის მიერ ნებისმიერი პროცესის შესრულებისას, რომლის შედეგადაც სისტემა უბრუნდება საწყის მდგომარეობას, შინაგანი ენერგიის სრული ცვლილება ტოლია ნულის. მათემატიკურად ეს ჩაიწერება ასე