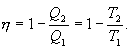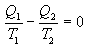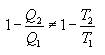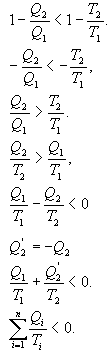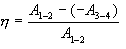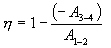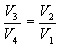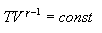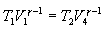განვიხილოთ შექცევადი და შეუქცევადი კარნოს ციკლები
შექცევადი კარნოს ციკლი. შექცევადი კარნოს ციკლისთვის მარგი ქმედების კოეფიციენტი ნებისმიერი ზემოთ მიღებული ფორმულით შეიძლება გამოითვალოს
აქედან
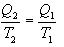
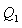
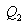
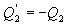
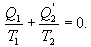 |
(10.25) |
სისტემაზე მიწოდებული სითბოს ფარდობა იმ ტემპერატურასთან, რომელზეც ეს ხდება, ეწოდება დაყვანილი სითბო. ამდაგვარად, 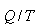
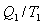
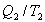
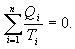 |
(10.26) |
რადგან შეიძლება ნებისმიერი შეკრული ციკლი წარმოვადგინოთ, როგორც უსასრულო ჯამი კარნოს ციკლებისა, ამიტომ ნებისმიერი შეკრული შექცევადი ციკლისთვის გამოსახულება (10.26) იქნება სამართლიანი და ის შეიძლება ჩავწეროთ ასე
| \(\oint_{L}^{ }\frac{\delta Q}{T}=0\) | (10.27) |
უკანასკნელ თანაფარდობას უწოდებენ კლაუზიუსის ტოლობას.
კარნოს შეუქცევადი პროცესი. ამ შემთხვევაში
და ყველა ტოლობა გარდაიქმნება უტოლობებად
| \(\oint_{L}^{ }\frac{\delta Q}{T}< 0\) | (10.28) |
(10.28) განტოლებას ეწოდება კლაუზიუსის უტოლობა.
გავაერთიანებთ რა (10.27)-სა და (10.28)-ს, მივიღებთ
| \(\oint_{L}^{ }\frac{\delta Q}{T}\leq 0\) | (10.29) |
ამდენად, ნებისმიერი ციკლის დაყვანილი სითბოების ჯამი ნულის ტოლია (შექცევადი პროცესი) ან ნულზე ნაკლებია (შეუქცევადი პროცესი).
თერმოდინამიკის პირველი კანონი ასახავს ენერგიის მუდმივობისა და ურთიერთგარდაქმნას მაგრამ არ იძლევა საშუალებას განისაზღვროს პროცესის მიმდინარეობის მიმართულება მართლაც ცივი სხეულიდან სხელ სხეულზე სითბოს თავისთავადი გადაცემის პროცესი არანაირად არ ეწინააღმდეგება თერმოდინამიკის პირველ კანონს. თუმცა გავარვარებული რკინის ნაჭრის ცივ წყალში ჩაშვებისას არასოდეს არ დაიკვირვება რკინის შემდგომი გაცხელება წყლის შესაბამისი გაციების ხარჯზე. და კიდევ, თერმოდინამიკის პირველი კანონი არ გამორიცხავს შესაძლებლობას ისეთი პროცესისა, რომლის ერთადერთი შედეგი იქნებოდა გამათბობლიდან მიღებული სითბოს მის ექვივალენტურ მუშაობად გარდაქმნა. ასე მაგალითად, პირველ კანონზე დაყრდნობით შეიძლებოდა გვეცადა პერიოდულად მოქმედი ძრავა, რომელიც შეასრულებდა მუშაობას სითბოს ერთი წყაროს ხარჯზე (მაგალითად ოკეანის შინაგანი ენერგიის ხარჯზე). ასეთ ძრავას ეწოდება მეორე გვარის მუდმივი ძრავა. უზარმაზარი ექსპერიმენტული მასალის განზოგადებამ მიგვიყვანა მეორე გვარის მუდმივი ძრავის შეუძლებლობის დასკვნამდე. ამ დასკვნას ეწოდა თერმოდინამიკის მეორე კანონი.
არსებობს თერმოდინამიკის მეორე კანონის რიგი ფორმით განსხვავებული და არსით ერთნაირი ფორმულირება:
1. შეუძლებელია პროცესი, რომლის ერთადერთი შედეგი არის გამათბობლიდან მიღებული მთელი სითბოს გარდაქმნა მის ექვივალენტურ მუშაობად.
2. კლაუზიუსის ფორმულირება: სითბო თავისთავად ვერ გადავა უფრო ნაკლებად გამთბარი სხეულიდან უფრო მეტად გამთბარ სხეულზე.
3. ტომსონ-პლანკის ფორმულირება: მეორე გვარის პერპენდუმ მობილე შეუძლებელია.
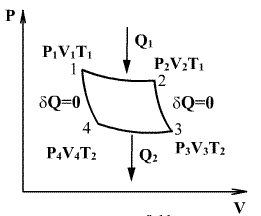
სითბური ძრავების მუშაობის ანალიზით, ფრანგი ინჟინერი სადი კარნო 1924 წელს მივიდა დასკვნამდე, რომ ყველაზე ხელსაყრელი წრიული პროცესი არის შექცევადი წრიული პროცესი, რომელიც შედგება ორი იზოთერმული და ორი ადიაბატური პროცესისგან, რადგან ისი ხასიათდება უდიდესი მარგი ქმედების კოეფიციენტით. ამ პროცესს ეწოდა კარნოს ციკლი. კარნოს პირდაპირ ციკლში მუშა სხეული იზოთერმულად, ხოლო შემდეგ ადიაბატურად ფართოვდება, რის შემდეგაც ისევ იზოთერმულად (უფრო დაბალ ტემპერატურაზე) და შემდეგ ადიაბატურად იკუმშება. ანუ კარნოს ციკლი შემოსაზღვრულია ორი იზოთერმითა და ორი ადიაბატით.
იზოთერმული გაფართოებისას გამათბობელს წაერთმევა 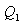
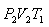
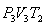
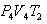
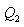
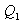
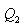
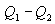
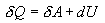
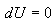
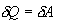
სასარგებლო მუშაობის ფარდობა გამათბობლის მიერ დახარჯულ ენერგიასთან განსაზღვრავს სითბური მანქანის მარგი ქმედების კოეფიციენტს (მქკ):
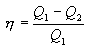 |
(10.23) |
ეს ფორმულა სამართლიანია ყველა შექცევადი და არაშექცევადი პროცესისთვის.
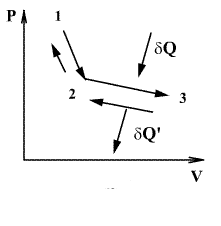
განვსაზღვროთ შექცევადი პროცესის კარნოს ციკლის მქკ. სითბო მიეწოდება უბანზე 1-2 და წაერთმევა უბანზე 3-4. იზოთერმული პროცესისთვის შინაგანი ენერგია U=const და მთელი მიწოდებული სითბო იხარჯება მუშაობაზე 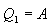
მაშინ
ანუ
იზოთერმული პროცესისთვის მუშაობა
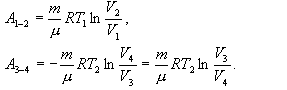
უკანასკნელი გამოსახულებების გათვალისწინებით
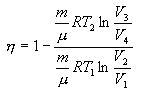 |
(10.24) |
ვაჩვენოთ, რომ
რადგან პროცესები უბნებზე 2-3 და 1-4 ადიაბატურებია, 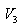
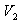
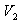
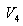
შესაბამისად,
და
გავყოთ ეს განტოლებები და მივიღებთ
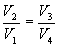
მაშინ მქკ-ს გამოსახულება (10.24) მიიღებს სახეს

ეს ფორმულა სამართლიანია მხოლოდ შექცევადი კარნოს ციკლისთვის.
კარნოს თეორემები.
1. ყველა კარნოს ციკლით მომუშავე შექცევად მანქანას, დამოუკიდებლად მუშა სხეულის ბუნებისა, აქვს ერთნაირი მქკ, იმ პირობით თუ მათ აქვთ საერთო გამათბობელი და მაცივარი.
2. თუ ორ სითბურ მანქანას აქვთ საერთო გამათბობელი და და მაცივარი და მათგან ერთი არის შექცევადი, ხოლო მეორე შეუქცევადი, მაშინ შექცევადის მქკ მეტია შეუქცევადის მქკ-ზე
ηშექც>ηშეუქც
შექცევადი ეწოდება პროცესს, რომელიც შეიძლება უკუ მიმართულებით ჩატარდეს ისე, რომ სისტემა გაივლის იგივე მდგომარეობებს რაც პირდაპირი სვლის დროს მაგრამ შებრუნებული თანმიმდევრობით. შექცევადი შეიძლება იყოს მხოლოდ წონასწორული პროცესი.
შექცევად პროცესს აქვს შემდეგი თვისებები: თუ პირდაპირი სვლისას რაიმე ელემენტურ უბანზე სისტემა იღებს 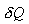
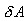
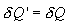
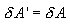
იმ შემთხვევაში, როცა პირდაპირი და შექცეული პროცესების დასრულების შემდექ სისტემა დაუბრუნდა საწყის მდგომარეობას და გარემომცველ გარემოში დარჩა ცვლილებები, პროცესი არის შეუქცევადი. აშკარაა, რომ ბუნებაში ყველა პროცესი არის შეუქცევადი.
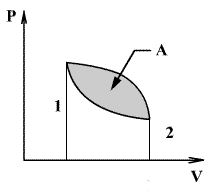
წრიული პროცესი (ანუ ციკლი) ეწოდება ისეთ პროცესს რომლის დროსაც სისტემა რიგი ცვლილებების შემდეგ უბრუნდება საწყის მდგომარეობას. გრაფიკზე ციკლი გამოსახულია შეკრული მრუდით. წრიული ციკლისას შესრულებული მუშაობა, რიცხობრივა ტოლია მრუდის მიერ შემოწერილი ფართობის. ციკლის შესრულების შემდეგ სისტემა უბრუნდება წინანდელ მდგომარეობას. ამიტომ მდგომარეობის ნებისმიერი ფუნქციას, კერძოდ შინაგან ენერგიას, აქვს ციკლის დასაწყისში და ბოლოში ერთნაირი მნიშვნელობა.