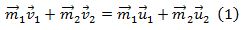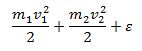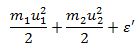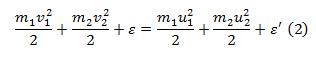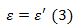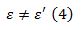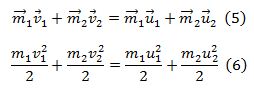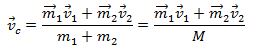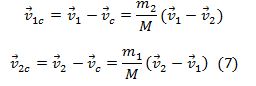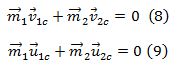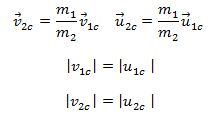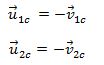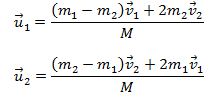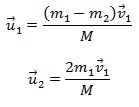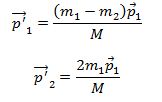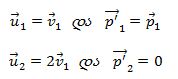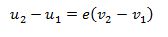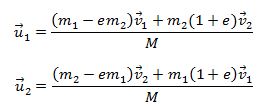თერმოდინამიკაში სხეულთა სითბური თვისებების დასახასიათებლად გამოიყენება სითბოტევადობის ცნება.
სითბოტევადობა არის სითბოს რაოდენობა, რომელიც საჭიროა სხეულის ერთი კელვინით გასათბობად. როგორც წესი სითბოტევადობა დამოკიდებულია მდგომარეობის დამახასიათებელ ყველა სიდიდეზე (წნევა მოცულობა და ტემპერატურა). ზოგადი განსაზღვრება არის:
| \(C\equiv \frac{\Delta Q}{\Delta T}\) | (10.11) |
სადაც Q არის დამატებული სითბოს რაოდენობა ხოლო \(\Delta T\) არის შედეგობრივი ტემპერატურის ნაზრდი. უფრო ზოგადად რადგან სითბოტევადობა დამოკიდებულია ტემპერატურაზე უნდა დავუშვათ, რომ ტემპერატურის ცვლილება არის იმდენად მცირე, რომ სითბოტევადობა არ იცვლება და მაშინ სითბოტევადობა ჩაიწერება ასე:
\(C\equiv \frac{\delta Q}{dT}\)
აქ δ სიმბოლო გულისხმობს იმას, რომ Q არის პროცესის ფუნქცია, ხოლო d კი იმას რომ T არის მდგომარეობის ფუნქცია.
კუთრ სითბოტევადობას უწოდებენ სიდიდეს, რომელიც რიცხობრივად ტოლია იმ სითბოსი, რაც უნდა მიეწოდოს სხეულის ერთეულოვან მასას რათა მისი ტემპერატურა ერთი კელვინით ამაღლდეს:
| \(C_{spec}=\frac{\Delta Q}{m\Delta T}\) | (10.12) |
აქედან შეიძლება განისაზღვროს სითბოს ის რაოდენობა, რაც საჭიროა m მასის სხეულის გასათბობად
| \(\Delta Q=C_{spec}m\Delta T\) | (10.13) |
მოლური სითბოტევადობა - სითბოს რაოდენობა, რომელიც საჭიროა ნივთიერების ერთ მოლის ერთი კელვინით გასათბობად
| \(C_{mol}=\frac{\Delta Q}{m\Delta T}\mu=C_{spec}\mu\) | (10.14) |
ღერმოდინამიკის პირველი კანონის გათვალისწინებით (10.11) ასე შეიძლება გადავწეროთ
| \(C=\frac{\mathrm{d} }{\mathrm{d} T}\left ( dU+\delta A \right )\) | (10.15) |
საიდანაც გამოდის, რომ სითბოტევადობა არის პროცესის ფუნქცია, ანუ სისტემის სითბოტევადობა დამოკიდებულია იმაზე თუ რანაირად გადადის სისტემა ერთი მდგომარეობიდან მეორეში. საზოგადოდ, ასეთი პროცესი შეიძლება იყოს ნებისმიერად ბევრი, ფაქტიურად კი ყველაზე ხშირად გამოიყენება სითბოტევადობა როცა р=const(Cp) და როცა V=const(CV).
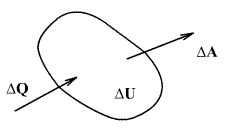
თერმოდინამიკის პირველი კანონი წარმოადგენს ენერგიის მუდმივობის კანონს. თუ სხეულს მივაწვდით ΔQ სითბოს რაოდენობას, ამ სითბოს ხარჯზე სხეულს შეუძლია გაზარდოს საკუთარი შინაგანი ენერგია ΔU სიდიდით და ამავდროულად შეასრულოს ΔA მუშაობა, ამსთან ენერგიის მუდმივობის კანონის თანახმად: ΔQ=ΔU+ΔA
უკანასკნელი გამოსახულება უფრო მოხერხებულია ჩაიწეროს სისტემაზე δQ მცირე სითბოს მიწოდებით გამოწვეული სისტემის მდგომარეობის მცირე ცვლილებისა და მის მიერ δA ელემენტური მუშაობის შესრულებისთვის
| δQ = dU+δA | (9.10) |
შინაგანი ენერგიის dU ნაზრდის ჩაწერასა და სითბოს δQ ელემენტური რაოდენობის ჩაწერასა და ასევე ელემენტური δA მუშაობის ჩაწერას შორის სხვაობა აიხსნება შემდეგი მოსაზრებით. როგორც უკვე აღვნიშნეთ, სისტემის შინაგანი ენერგია არის მისი მდგომარეობის ფუნქცია. შესაბამისად, ნებისმიერი პროცესისას, რომლის შედეგადაც სისტემა კვლავ უბრუნდება რომელიმე მდგომარეობას, მისი შინაგანი ენერგიის სრული ცვლილება ნულის ტოლია. მათემატიკურად ეს ჩაიწერება ამ განტოლების სახით 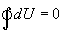
ამდენად:
δQ = dU+δA
თერმოდინამიკის პირველკი კანონი ჩამოყალიბდება ასე:
სისტემაზე გადაცემული სითბო იხარჯება სისტემის შინაგანი ენერგიის ზრდაზე და მუშაობის შესრულებაზე.
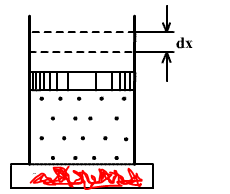
განვიხილოთ აირი დგუშიან ცილინდრში, რომლის მოცულობის ცვლილებაც არის შესაძლებელი. აღვნიშნოთ, რომ აქ სიტყვა "აირი" პირობითია. ეს შეიძლება იყოს სითხე, კრისტალი და საერთოდ ნებისმიერი სხეული. ცილინდრი კონტაქტში არის გამაცხელებელთან, რომელსაც შეუძლია აირს გადასცეს ან წაართვას სითბო.
ვთქვათ დგუშზე გარედან მოქმედებს ნებისმიერი სიდიდის დაწოლა.
ყველა პროცესი, რომელსაც ქვევით განვიხილავთ, იქნება კვაზისტატიკური, ანუ იმდენად ნელი, რომ დროის ნებისმიერ მომენტში აირი შეიძლება ჩაითვალოს თერმოდინამიკურ წონასწორობაში. თუ აირს ძალიან სწრაფად შევკუმშავთ, მაშინ დგუშთან რაღაც მომენტში წნევა აღმოჩნდება მეტი ვიდრე დანარჩენ მოცულობაში და მაშინ შეუძლებელი იქნება აირის წნევაზე საზოგადოდ საუბარი. ასეთი პროცესი არ არის კვაზისტატიკური. დაახლოებით კვაზისტატიკურად ითვლება პროცესებიც, რომლებიც საკმაოდ სწრაფად მიმდინარეობენ ტექნიკური თვალსაზრისით, მაგალითად პროცესები, რომლებიც მიმდინარეობენ ავტომანქანების ძრავების ცილინდრებში (ირკვევა, რომ კვაზისტატიკურობისთვის საჭიროა, დგუშის სიჩქარე ნაკლები იყოს აირში ბგერის სიჩქარეზე).
აირზე მუშაობა სრულდება მისი შეკუმშვისას. თვით აირი მუშაობას ასრულებს გაფართოებისას. ვთქვათ აირი ფართოვდება ისე, რომ დგუში ადის dx სიდიდით ზევით. მაშინ აირი ასრულებს მუშაობას 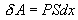
 |
(9.8) |
ამ სიდიდეს ეწოდება აირის ელემენტური მუშაობა. აირის V1 მოცულობიდან V2 მოცულობამდე გაფართოებისას შესრულებული მუშაობა ტოლი იქნება
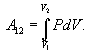 |
(9.9) |
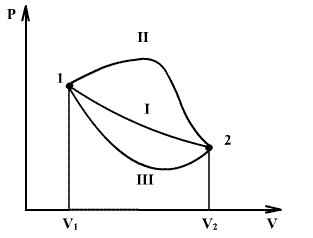
თუ ერთ ღერძზე გადავზომავთ აირის V მოცულობას, მეორეზე – მის P წნევას, მუშაობა გამოისახება P(V) მრუდის ქვეშ მოქცეული ფართობით.
V1 მოცულობიდან V2 მოცულობამდე გაფართოების პროცესი შეიძლება მიმდინარეობდეს სხვადასხვანაირად: მაგალითად, შეიძლება ამ დროს აირის იზოლირება გამათბობელისგან ან, პირიქით, გავათბოთ აირი და ა.შ. სხვაგვარად, რომ ვთქვათ, წერტილი 1-დან წერტილ 2-ში გადაადგილებისას აირში შეიძლება მიმდინარეობდეს სხვადასხვა პროცესები, მაშინაც კი თუ დავაფიქსირებთ საწყის და საბოლოო მდგომარეობებს. ყოველ პროცესში მუშაობას ექნება საკუთარი მნიშვნელობა, რადგან მრუდის ქვეშ ფართობები იქნება განსხვავებული (მრუდები I, II, და III). ამდენად, აირის მიერ შესრულებული მუშაობა დამოკიდებულია პროცესზე, რომელიც მასში მიმდინარეობს. ჩვეულებრივ ამბობენ, რომ "აირის მუშაობა არის პროცესის ფუნქცია".
აღვნიშნოთ, რომ მუშაობა დადებითია, თუ მას ასრულებს აირი და უარყოფითია, თუ გარე ძალები ასრულებენ მას აირზე.
მოამზადა: ზურაბ ვაშალომიძემ
ნაწილაკების ურთიერთქმედების ერთ–ერთი მნიშვნელოვანი შემთხვევა დაჯახებაა. საწყის მომენტში ვთქვათ სხეულები არ ურთიერთქმედებენ, დაჯახების შემდეგ ერთმანეთს გადასცემენ იმპულსს და ენერგიას, თან შორდებიან ერთმანეთს სხვა მიმართულების და სიდიდის სიჩქარით. დაჯახების უამრავი მაგალითი შეგვიძლია ჩამოვთვალოთ: ბირთვების დრეკადი და არადრეკადი დაჯახება, ელექტრონის დაჯახება ატომთან ან მოლეკულასთან, და სხვა.
დაჯახებაზე მსჯელობისას გულისხმობენ რომ ნაწილაკები რაღაც მომენტში ეხებიან ერთმანეთს, მაგრამ თანამედროვე გაგებით ნაწილაკების აგებლების გამო არ შეიძლება ვილაპარაკოთ მათი ბირთვების შეხებაზე. ვთქვათ ლითონის ბირთვების დაჯახებისას, იმას რასაც ჩვენ დაჯახებას ვეძახით არის მცირე მანძილზე დაახლოება. იმ მანძილზე სადაც განზიდვის ძალები იმდენად დიდია რომ არ აძლევენ საშუალებას უფრო დაახლოების. დაჯახების ძირითადი ამოცანა მდგომარეობს ნაწილაკების დაჯახების შემდგომ სიჩქარის დადგენა. ამოცანის ამოხსნისთვის საჭიროა ვიცოდეთ რა ხდება დაჯახების არეში. სიჩქარის დადგენა მხოლოდ იმპულსის და ენერგიის მუდმივობის კანონის ფარგლებში უნდა მოხდეს.
განვიხილოთ 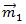
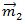
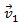
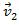
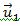
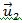
მეორე კანონი ენერგიის მუდმივობის კანონი სამი ნაწილისაგან შედგება: შინაგანი ენერგიის ჯამი, პოტენციური ენერგია და კინეტიკური ენერგია. შინაგანი ენერგიის ჯამი ავღნიშნოთ დაჯახებამდე 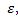
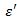
დაჯახების შემდეგ:
ენერგიის მუდმივობის კანონის თანახმად:
იმის მიხედვით თუ როგორია შინაგანი ენერგია განსაზღვრავენ დაჯახების სხვადასხვა ტიპებს:
- დრეკადი დაჯახება ეწოდება ისეთ დაჯახებას რომელის დროსაც ნაწილაკთა შინაგანი ენერგიები არ იცვლება.
- არადრეკადი დაჯახება ისე დაჯახებას ეწოდება, რომლის დროსაც ხდება ნაწილაკთა შინაგანი ენერგიის ცვლილება.
არადრეკადი დაჯახება თავის მხრივ ორი სახისაა: პირველი გვარის არადრეკადი დაჯახება როდესაც დაჯეხების შემდეგ შინაგანი ენერგია მატულობს, კინეტიკური ენერგიის ნაწილი იხარჯება შინაგანი ენერგიის გაზრდაზე. მეორე გვარის არადრეკადი დაჯახება როდესაც შინაგანი ენერგია მცირდება, შინაგანი ენერგიის ნაწილო გაგდადის კინეტიკურ ენერგიაში.
განვიხილოთ ორი ნაწილაკის დაჯახება, ასეთი დაჯახების დროს იმპულსი და ენერგია მუდმივია.
ვიცით საწყისი სიჩქარეები უნდა ვიპოვოთ საბოლოო. რადგან სიჩქარე ვექტორია და დაიშლება სამ მდგენელად (5) და (6) ერთად ოთხი განტოლება იქნება. თუმცა ეს ინფორმაცია არაა სრული ამოცანის ამოხსნისთვის საჭიროა ვიცოდეთ ურთიერთქმედება დაჯახების შემდეგ. თუმცა თავიდანვე ურთიერთქმედება გამოვრიცხეთ, იმისთვის რომ ამოვხსნათ განტოლებათა სისტემა საჭიროა ვიცოდეთ დაჯახებამდე სიჩქარეები და ერთ–ერთი სხეულის მიმართულება დაჯახების შემდგომ. მოსაძებნი დაგვრჩება მეორე ნაწილაკის ვექტორული სიჩქარე და პირველი ნაწილაკის სიჩქარის სკალარული სიდიდე. დასმული ამოცანის ამოსახსნელათ შემოვიღოთ ინერციული სისტემა რომლის სათავე მოთავსებულია ნაწილაკთა ინერციის ცენტრში და ამ ინერციის ცენტრთან ერთად მოძრაობს. შევისწავლოთ დაჯახება ამ სისტემაში, რომელსაც C სისტემა ვუწოდოთ და შემდეგ დავუბრუნდეთ ისევ ძველ სისტემას, ანუ L სისტემას. ინეტციის ცენტრის სიცქარის ფორმულის თანახმად:
იმისთვის რომ გავიგოთ C ციცტემის მიმართ სიჩქარეები L სისტემის მიმართ სიჩქარეებს ვაკლებთ C სისტემის სიჩქარეს.
გამოვთვალოთ სიჩქარეები C სისტემაში.
ცხადია რომ საერთო იმპულსი ნულის ტოლია.
ის მომენტი რომ დაჯახებამდეც და დაჯახების შემდეგაც იმპულსი ნულია ამარტივებს დაჯახების შესწავლას.
ზედა ფორმულებიდან ვასკვნით რომ სიჩქარეების სიდიდეები უცვლელი რჩება. რაც შეეხება მიმართულებას საჭიროა ვიცოდეთ ურთიერთქმედების ხასიათის და დაჯახების პარამეტრების ცოდნა.
ახლა განვიხილოთ ცენტრალური დრეკადი დაჯახება, დაჯახების შემდეგ სიჩქარეები მიმართულია საწყისი სიჩქარეების საწინააღმდეგოდ.
ამიტომ გვექნება
თუ განვიხილავთ შემთხვევას როდესაც მეორე ნაწილაკი დაჯახებამდე უძრავია 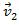
ხოლო იმპულსებისთვის გვექნება:
თუ ამ ფორმულებს მასების სხვადასხვა შეფარდებისთვის გავარჩევთ გვექნება:
- თუ m1<m2 ამ შემთხვევაში საბოლოო სიჩქარე მიმართულია საწყისის საწინააღმდეგოდ, ე.ი დამჯახებელი ნაწილაკი უკან დაბრუნდება.
- თუ m1>m2 მაშინ პირველი სხეულის საბოლოო იმპულსი იქნება საწყისი იმპულსის გასწვრივ მიმართული და ნაწილაკი განაგრძობს მოძრაობას საწყისი მიმართულებით.
- თუ m1=m2 ამ შემთხვევაში პირველი ნაწილაკი ჩერდება ხოლო მეორე რომელიც უძრავი იყო იწყებს მოძრაობას იგივე სიჩქარით და იმპულსით როგორიც ქონდა პირველს.
თუ უფრო კერძო შემთხვევას განვიხილავთ მაგალითად დამჯახებელი ნაწილაკის მასა იმდენად მცირეა რომ უგულებელვყოთ მაშინ გვექნება 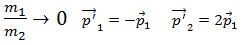
მეორე შემთხვევა იქნება თუ ძალიან დიდი მასის ნაწილაკი ძალიან მცირე მასის ნაწილაკს ეჯახება 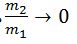
ამ შემთხვევაში დამჯახებელი ნაწილაკი იმავე სიჩქარით და იმპულსით განაგრძობს მოძრაობას, ხოლო უძრავი ნაწილაკი განაგრძობს ორჯერ მეტი სიჩქარით მოძრაობას მაგრამ ნულოვანი იმპულსით.
დრეკადი დაჯახების ერთ–ერთი მახასიათებელი თვისების გამოსაყვანათ, გამოვითვალოთ ფარდობითი სიჩქარე, ე.ი სიჩქარეების სხვაობა დაჯახების შემდეგ და ვნახავთ რომ დაჯახების შემდეგ სიჩქარის სიდიდეები არ იცვლება იცვლება მხოლოდ მიმართულება.
თუ განვიხილავთ არადრეკად დაჯახებას მაშინ შინაგანი ენერგია იცვლება და მაშასადამე იცვლება სიცქარეებიც ა რათქმაუნდა შეიცვლება ფარდობითი სიჩქარეც. საკითხს თუ როგორ იცვლება ფარდობითი სიდიდე არადრეკადი დაჯახებისას დააკვირდა ნიუტონი. ყოველი არადრეკადი დაჯახებისას ფარდობითი სიჩქარე იცვლება e–ჯერ ანუ განყენებულ რიცხვჯერ, როომელიც სხეულის გვარობაზეა დამოკიდებული. ამ სიდიდეს აღდგენის კოეფიციენტი ეწოდა.
თუ:
- e=1 დაჯახება დრეკადია
- e<1 პირველი გვარის არადრეკადი დაჯახება
- e>1 მეორე გვარის არადრეკადი დაჯახება
არადრეკადი დაჯახებისთვის მივიღებთ რომ სიჩქარეები ტოლია:
კერძო შემთხვევების განხილვით გავიგებთ კინეტიკური ენერგიების ცვლილებას.
ერთ–ერთი ფრიად მნიშვნელოვანი მოვლენა რაც ნაწილაკების დაჯახებასთანაა დაკავშირებული არის ნაწილაკის დაშლა. რეალურ ცხოვრებაში ან ბუნებაში ხშირად ვხვდებით მოვლენას როდესაც ნაწილაკი ან სხეული იშლება რამდენიმე ნაწილად და წარმოშობილი ნაწილები იწყებს მოძრაობას სხვადასხვა სიჩქარით.
თუ განვიხილავთ უძრავი ნაწილაკის დაშლას ორ ნაწილაკად ეს მოვლენა აბსოლუტურად არადრეკადი დაჯახების შებრუნებულია.
ორ ნაწილაკად დაშლის ენერგიამ შეიძლება ცალსახად მოგვცეს დაშლილი ნაწილაკების სიჩქარეები რაც არ ხდება სამ ნაწილად დაშლის შემთხვევაში.