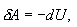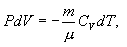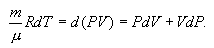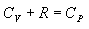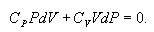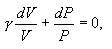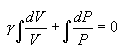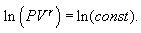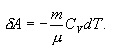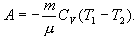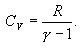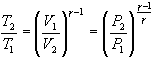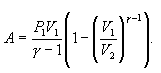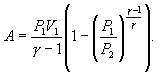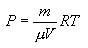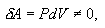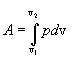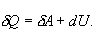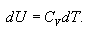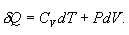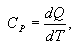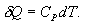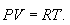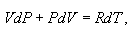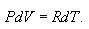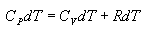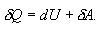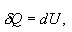ადიაბატური პროცესი - აირის მდგომარეობის ისეთი ცვლილებაა, რომლის დროსაც ის არც გასცემს გარემოში და არც იღებს გარემოსგან სითბოს. შესაბამისად, ადიაბატური პროცესი ხასიათთდება გარემოსთან სითბოცვლის არარსებობით. ადიაბატურად შეიძლება ჩაითვალოს სწრაფად მიმდინარე პროცესები. რადგან ადიაბატური პროცესის დროს სითბოს გადაცემა არ ხდება, ამიტომ 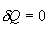
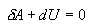 |
(10.20) |
ანუ
ე.ი. აირი ასრულებს მუშაობას შინაგანი ენერგიის ცვლილების გამო. აირის ადიაბატურ გაფართოებას (dV>0) ახლავს დადებით გარე მუშაობა, მაგრამ ამასთან აირის შინაგანი ენერგია მცირდება და აირი ცივდება (dT<0).
აირის შეკუმშვას (dV<0) თან ახლავს აირის გათბობა.
ვიპოვნოთ იდეალური აირის მდგომარეობის პარამეტრებს (მაგალითად, Р და V) შორის კავშირი ადიაბატური პროცესის დროს. ამისთვის გადავწეროთ (10.20) ამ ფორმით
სიდიდე 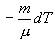
ამდენად,
\(PdV=-\frac{C_{V}}{R}\left ( PdV+VdP \right )\),
ანუ, გავითვალისწინებთ რა, რომ იდეალური აირისთვის
ამ განტოლების ორივე მხარე გავყოთ 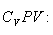
სადაც \(\gamma =\frac{C_{p}}{C_{V}}\) უგანზომილებო სიდიდეა, რომელსაც ადიაბატის მუდმივა ეწოდება.  -ს ტემპერატურაზე დამოკიდებულების უგულებელყოფით, შეიძლება ჩაითვალოს, რომ მოცემული აირისთვის
-ს ტემპერატურაზე დამოკიდებულების უგულებელყოფით, შეიძლება ჩაითვალოს, რომ მოცემული აირისთვის 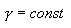
უკანასკნელი განტოლების ინტეგრირებით
მივიღებთ
ანუ
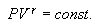 |
(10.21) |
ამ გამოსახულებას ეწოდება პუასონის განტოლება.
წნევასა და ტემპერატურას შორის კავშირის დასადგენად ჩავსვათ (10.21)-ში V-ს გამოსახულება კლაპეირონის განტოლებიდან, მივიღებთ
\(P^{\left ( 1-\gamma \right )}T^{\gamma }=const\)
ამ უკანასკნელში (10.21)-ის გათვალისწინებით შეგვიძლია მივიღოთ -სა და -ს შორის დამოკიდებულება
\(V^{\left ( \gamma \right -1)}T=const\)
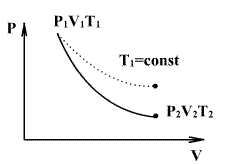
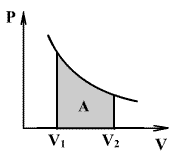
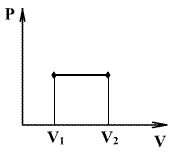
მდგომარეობის დიაგრამეზე ადიაბატური პროცესის აღმწერი წირს უწოდებენ ადიაბატას. ნახაზზე უწყვეტი წირით ნაჩვენებია ადიაბატა (P-V) დიაგრამაზე. შესადარებლად იგივე ნახაზზე წყვეტილი წირით გამოსახულია იზოთერმა, რომელიც აირის საწყის 1 მდგომარეობაში ტემპერატურას შეესაბამება. რადგან ნებისმიერი იდეალური აირისთვის ადიაბატის მაჩვენებელი 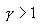
ადიაბატური პროცესისას აირის მიერ შესრულებული მუშაობის მოსაძებნად ვაინტეგრებთ გამოსახულებას
სრული მუშაობა არის
მაიერის განტოლებიდან (10.18) და γ ადიაბატის მაჩვენებლის გამოსახულებიდან 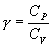
ამიტომ
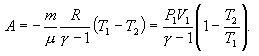 |
(10.22) |
VT PT VP თანაფარდობების თანახმად
შესაბამისად, მუშაობისთვის გამოსახულება(10.22) შეიძლება წარმოვადგინოთ ასე
ანუ
იზოთერმული პროცესის დროს (Т=const) dT=0 და შინაგანი ენერგიის ცვლილება dU=0. თერმოდინამიკის პირველი კანონის თანახმად აირზე გადაცემული სითბო δQ სრულად იხარჯება მუშაობის შესრულებაზე δQ=δA.
სისტემის მუშაობა რიცხობრივად ტოლია P:V კოორდინატებში პროცესის მრუდის ქვეშ მყოფი ფართობის. მუშაობისთვის ანალიზურ გამოსახულებას აქვს სახე: best female viagra uk
კლაპეირონის განტოლებიდან განვსაზღვ როთ Р:
და ჩავსვათ მუშაობის განტოლებაში
| \(A=\frac{mRT}{\mu }\int_{V_{1}}^{V_{2}}\frac{1}{V}dV=\frac{mRT}{\mu }ln\frac{V_{2}}{V_{1}}\) | (10.19) |
იზობარული პროცესის დროს P=const და ელემენტური მუშაობა
სისტემის მუშაობა მოცულობის V1-დან V2 -მდე ცვლილებისას განისაზღვრება ასეთნაირად
თერმოდინამიკის პირველი კანონის განტოლებას აქვს სახე
შესაბამისად, იზობარული პროცესის დროს აირზე გადაცემული სითბო იხარჯება მისი შინაგანი ენერგიის ზრდაზე და მუშაობის შესრულებაზე. (10.16)-დან გამოდის, რომ აირის ერთი მოლისთვის:
თავის მხრივ 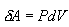
განსაზღვრების თანახმად იზობარული მოლური სითბოტევადობა
საიდანაც
ჩავსვათ უკანასკნელი თერმოდინამიკის პირველ კანონში, მივიღებთ
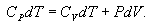 |
(10.17) |
განვსაზღვროთ Р წნევა იდეალური აირის მდგომარეობის განტოლებიდან ერთი მოლი აირისთვის, მივიღებთ:
გავადიფერენციალოთ ყველა პარამეტრით:
რადგან p= const, ამიტომ dP = 0 და აირის მდგომარეობის განტოლებას აქვს სახე:
ჩავსვათ უკანასკნელი (10.17)-ში
ანუ
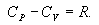 |
(10.18) |
უკანასკნელ თანაფარდობას ეწოდება მეიერის განტოლება.
თერმოდინამიკის პირველი კანონი
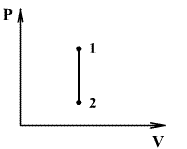
რადგან იზოქორული პროცესის დროს მუშაობა არ სრულდება
თერმოდინამიკის პირველი კანონი იძენს შემდეგ სახეს:
ანუ იზოქორული პროცესის დროს აირზე მიწოდებული სრული სითბო იხარჯება სისტემის შინაგანი ენერგიის ზრდაზე. სითბოტევადობას აქვს სახე
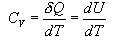 |
(10.16) |
თუ პროცესის დროს სისტემის ტემპერატურა შეიცვალა T1 მნიშვნელობიდან T2 მნიშვნელობამდე, მაშინ პროცესის დროს გადაცემული სითბოს რაოდენობისთვის (10.16)-ის მეშვეობით შეგვიძლია დავწეროთ:
| \(\Delta Q=\int_{T_{1}}^{T_{2}}C_{V}dT=C_{V}\Delta T\) | (10.16.1) |
კუთრი სითბოდევადობის გამოყენებით განტოლება (10.13)-ის თანახმად (10.16.1) შეიძლება გადავწეროთ ასე
| \(\Delta Q=mC_{Vspec}\Delta T\) | (10.16.2) |