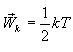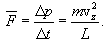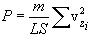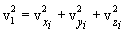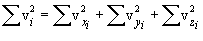მოლეკულები შეიძლება განვიხილოთ როგორც მატერიალურ წერტილთა (ატომების) სისტემები, რომლებიც ასრულებენ როგორც გადატანით ასევე ბრუნვით მოძრაობებს. სხეულის მოძრაობის შესასწავლად უნდა ვიცოდეთ მისი მდებარეობა არჩეული კოორდინატთა სისტემის მიმართ. ამისთვის შემოაქვთ სხეულის თავისუფლების ხარისხის ცნება. დამოუკიდებელ კოორდინატთა რიცხვი, რომელიც სრულად განსაზღვრავს სხეულის სივრცეში მდებარეობას, სხეულის თავისუფლების ხარისხი ეწოდება.
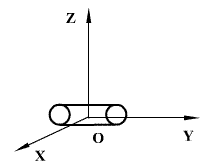
წერტილის წრფეზე მოძრაობისა მისი მდებარეობის შესაფასებლად უნდა ვიცოდეთ მისი ერთი კოორდინატი, ანუ სხეულს აქვს თავისუფლების ერთი ხარისხი. თუ სხეული მოძრაობს სიბრტყეზე, მისი მდებარეობა ხასიათდება ორი კოორდინატით; ამ შემთხვევაში წერტილს აქვს ორი თავისუფლების ხარისხი. სივრცეში წერტილის მდებარეობა განისაზღვრება სამი კოორდინატით. თავისუფლების ხარისხი ჩვეულებრივ აღინიშნება i ასოთი. მოლეკულები, რომლებიც ჩვეულებრივ შედგებიან ერთი ატომისგან, ითვლებიან მატერიალურ წერტილებად და აქვთ სამი თავისუფლების ხარისხი (არგონი, ჰელიუმი).
ორატომიან ხისტ მოლეკულებს, მაგალითად წყალბადის, აზოტის და სხვ. მოლეკულებს აქვთ ხუთი თავისუფლების ხარისხი: მათ აქვთ გადატანითი მოძრაობის 3 თავისუფლების ხარისხი და ОХ და OZ ღერძების მიმართ ბრუნვის 2 თავისუფლების ხარისხი. OY ღერძის მიმართ ბრუნვა შეიძლება უგულებელვყოთ, რადგან მისი ინერციის მომენტი ამ ღერძის მიმართ ძალიან მცირეა. ამიტომ ორატომიანი მოლეკულის OY ღერძის ირგვლივ ბრუნვიი მოძრაობის ენერგიის წვლილი ჯამურ ენერგიაში შეიძლება არ გავითვალისწინოთ.
ერთ წრფეზე არ მყოფი სამი და მეტი ატომისგან ხისტად შედგენილ მოლეკულებს აქვთ თავისუფლების ხარისხი i = 6: გადატანითი მოძრაობის 3 ხარისხი და ОХ, OY და OZ ღერძების ირგვლივ ბრუნვის 3 ხარისხი.
ამ შემთხვევაში, თუ ატომებს შორის დაშორებები შეიძლება იცვლებოდეს (არახისტი კავშირი), მაშინ ჩნდება თავისუფლების დამატებითი ხარისხები.
აირების მოლეკულურ-კინეტიკური თეორიის თანახმად მოლეკულების მოძრაობას აქვს ქაოტური ხასიათი; ეს უწესრიგობა ეხება მოძრაობის ყველა სახეობას. მოძრაობის არცერთ სახეს არ აქვს სხვის მიმართ უპირატესობა. სტატისტიკური წონასწორობისას მოძრაობის ენერგია საშუალოდ თანაბრად ნაწილდება ყველა სახის მოძრაობაზე. მოლეკულის თავისუფლების ხარისხებზე ენერგიის თანაბარი განაწილების კანონი ასე შეიძლება ჩამოყალიბდეს: სტატისტიკურად საშუალოდ მოლეკულის თავისუფლების ყოველ ხარისხზე მოდის ერთნაირი ენერგია. მოლეკულის გადატანითი მოძრაობა ხასიათდება საშუალო კინეტიკური ენერგიით, რომელიც ტოლია 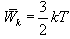
ერთგვაროვან აირში, რომლის მოლეკულებსაც აქვთ ნებისმიერი i თავისუფლების ხარისხი, ყოველ მოლეკულას აქვს საშუალოდ მოძრაობის ენერგია, ტოლი
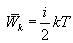 |
(11.11) |
იდეალური აირების მოლეკულურ-კინეტიკური თეორიის ძირითადი განტოლება ეწოდება განტოლებას, რომელიც აირის წნევას განსაზღვრავს. მნიშვნელოვანი აქ არის განისაზღვროს ტემპერატურის მოლეკულურ-კინეტიკური არსი. მომავლისთვის დაგვჭირდება მოლეკულების კონცენტრაციის ცნება. კონცენტრაციას ვუწოდებთ მოცულობის ერთეულში მოლეკულების n რაოდენობას
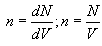 |
(11.1) |
პირველი ფორმულა სამართლიანია ყოველთვის, მეორე – მაშინ, როცა მოცულობაში კონცენტრაცია ყველგან ერთნაირია.
კონცენტრაციით შეიძლება ასევე აირის წნევის გამოსახვა 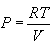
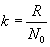
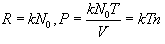
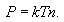 |
(11.2) |
აუცილებელია ამავე განტოლების გამოყვანა მოლეკულურ-კინეტიკური თეორიიდანაც, სხვა სიტყვებით რომ ვთქვათ, ვიპოვნოთ აირის წნევა კედელზე. წნევა არის მოლეკულების კედელზე შეჯახებების შედეგი. ერთი წამის განმავლობაში ყველა მოლეკულის მიერ კედელზე გადაცემული იმპულსი არის სწორედ წნევის ძალა, ანუ PS, სადაც S არის კედლის ფართობი. რადგან მოლეკულის ყოველი შეჯახებისას სრული იმპულსი ინახება, წნევის გამოსათვლელად საჭირო არ არის მოლეკულებს შორის შეჯახებების გათვალისწინება.
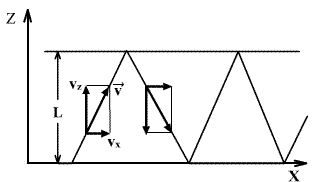
განვიხილოთ მოლეკულა, რომელიც მოძრაობს L მანძილით დაშორებულ კედლებიანი ჭურჭლის კედლებს შორის. ზედა კედელთან შეჯახების შედეგად იცვლება მხოლოდ სიჩქარის vz მდგენელი. ეს მდგენელი იცლება 2vz სიდიდით.
მოლეკულის იმპულსის ცვლილება დაჯახებისას (ანუ კედელზე გადაცემული იმპულსი) ტოლია δp=2mvz . იმპულსის ეს ცვლილება ხდება დროის Δt შუალედში, რომელიც სჭირდება მოლეკულას კედლებზე ორ შეჯახებას შორის და ტოლია 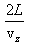
ამდენად, ერთი მოლეკუა კედელზე მოქმედებს საშუალო ძალით
სხვადასხვა მოლეკულებს სხვადასხვა სიჩქარეები აქვთ, ამიტომ 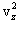
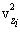
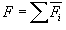
ახლა ჩავწეროთ
ავჯამოთ ყველა N მოლეკულით
x,y,z ღერძთა თანაბარუფლებიანობის გამო თერმოდინამიკური წონასწორობის დროს მარჯვენა სამი ჯამი (მოლეკულების დიდი რიცხვის შემთხვევაში) ერთმანეთის ტოლია, საიდანაც
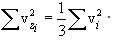
შემოვიღოთ საშუალო კვადრატული სიჩქარის ცნება (მას ასევე სითბურ სიჩქარეს უწოდებენ vi ). ამისთვის აუცილებელია სიჩქარის საშუალო კვადრატის მოძებნა. ის, ცხადია, ტოლია
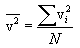 |
(11.3) |
გამოსახულება (11.3) სრულიად ანალოგიურია საშუალო არითმეტიკული სიჩქარის გამოსახულებისა
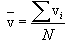 |
(11.4) |
მხოლოდ (11.4)-ში იკრიბება მოლეკულების სიჩქარეების აბსოლუტური სიდიდეები, ხოლო (11.3)-ში – სიჩქარის კვადრატები.
საშუალოკვადრატული, ანუ სითბური სიჩქარე ეწოდება (11.3) გამოსახულების კვადრატულ ფესვს:
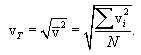 |
(11.5) |
აღვნიშნოთ, რომ 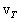
აირების მკთ განტოლების გამოყვანას დავუბრუნდეთ და (11.3)-ის გამოყენებით ჩავწეროთ:
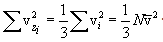
მიღებული გამოსახულება ჩავსვათ P-ს გამოსახულებაში, მივიღებთ
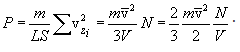
ბოლოს, იმის გათვალისწინებით, რომ 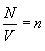
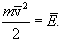
| \(P=\frac{2}{3}n\bar{E}_{k}\) | (11.6) |
სწორედ ეს არის იდეალური აირის მკთ ძირითადი განტოლება ის ასე იკითხება: აირის წნევა ერთეულოვან მოცულობაში მოქცეული მოლეკულების გადატანითი მოძრაობის კინეტიკური ენერგიის 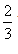
(11.6)-ის (11.2)-თან შედარებით, მივიღებთ ძალიან მნიშვნელოვა ტოლობას
| \(\bar{E}_{k}=\frac{3}{2}kT\) | (11.7) |
ეს გამოსახულება ხსნის ტემპერატურის ცნების მოლეკულურ-კინეტიკურ არსს.
ტემპერატურა – ეს არის მოლეკულების მოძრაობის საშუალო კინეტიკური ენერგია (გამოსახული სხვა ერთეულებში).
ამ განსაზღვრებაში ძალიან მნიშვნელოვანია სიტყვა "საშუალო". თუ აირს ამოვაცლით ყველაზე ნელ მოლეკულას, ყველა მოლეკულის სრული კინეტიკური ენერგია მცირდება, მაგრამ ტემპერატურა იზრდება, რადგან იზრდება საშუალო კინეტიკური ენერგია.
ჩავწეროთ
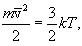 |
(11.8) |
აქედან ვიპოვნით მოლეკულის საშუალოკვადრატულ სიჩქარეს
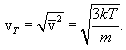 |
(11.9) |
ეს სიჩქარე ტემპერატურიდან კვადრატული ფესვის პროპორციულია.
(11.9) შეიძლება ასე ჩავწეროთ
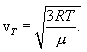 |
(11.10) |
ჟანგბადის მოლეკულისთვის (μ=0,032 კგ/მოლი) როცა Т=300К vТ=483 მ/წმ. წყალბადის მოლეკულისთის (μ=0,002 კგ/მოლ) ამავე ტემპერატურაზე სიჩქარე ტოლია vТ=1932 მ/წმ, ანუ ის მეტია ჟანგბადის მოლეკულის სიჩქარეზე 4-ჯერ.
ძალიან მნიშვნელოვანია ის გარემოება, რომ თერმოდინამიკური წონასწორობის პირობებში მოლეკულის საშუალო კინეტიკური ენერგია (11.8) არ არის მოლეკულის მასაზე დამოკიდებული. თუ შევურევთ რამოდენიმე აირს, მაგალითად Н2, О2 და წყალბადის მოლეკულაზე ასჯერ უფრო მძიმე მოლეკულებიან აირს მაშინ თერმოდინამიკური წონასწორობის პირობებში ყველა გაზის საშუალო კინეტიკური ენერგია იქნება ერთმანეთის ტოლი. მძიმე მოლეკულები იმოძრავებენ მცირე სიჩქარეებით, ისეთით, რომ მათი საშუალო კინეტიკური ენერგია ზუსტად ტოლი იყოს მსუბუქი მოლეკულების საშუალო კინეტიკური ენერგიისა.
სითხეში ბროუნის ნაწილაკების საშუალო კინეტიკური ენერგი, ამ ნაწილაკების უზარმაზარი მასის მიუხედავად (მოლეკულების მასასთან შედარებით) ისეთივეა როგორის მოლეკულებისა.
შეიძლება განვიხილოთ მძიმე და მსუბუქი აირები, როგორც ორი ერთმანეთთან თერმოდინამიკურ წონასწორობაში მყოფი სისტემა. თერმოდინამიკური წონასწორობა გულისხმობს ამ სისტემების ტემპერატურების ტოლობას. წინააღმდეგ შემთხვევაში სითბო გადაეცემა უფრო ცხელი სისტემიდან უფრო გრილ სისტემას.
მოლეკულურ-კინეტიკური თეორიის ამოცანა არის ნივთიერების მოლეკულურ-კინეტიკური მოდელით მისი ყველა თვისების გამოყვანა. ეს მოდელი შეიცავს წარმოდგენებს ნივთიერების მოლეკულების თვისებებზე, მათ მოძრაობებზე და ურთიერთქმედებებზე. წარმოდგენები, ბუნებრივია, ზუსტდება მეცნიერების განვითარებასთან ერთად და ზუსტდება მოდელიც.
ამ მოდელის ძირითადი დებულებებია:
- აირი შედგება მოლეკულებისგან
- აირის მოლეკულები მუდმივ ქაოსურ მოძრაობას ასრულებენ
- მოლეკულები ეჯახებიან ერთმანეთს. დაჯახებები არის დრეკადი (დაბალი ტემპერატურები) და არადრეკადი (მაღალი ტემპერატურები)
- დაჯახებებს შორის შუალედებში მოლეკულები მოძრაობენ წრფივად
- მოლეკულები მცირე დაშორებებზე ურთიერთგანიზიდებიან, ხოლო დიდ დაშორებებზე ურთიერთმიიზიდებიან.
აღსანიშნავია, რომ თვით მოლეკულის შინაგანი სტრუქტურა აღიწერება ქვანტური ფიზიკით.
მოამზადა: თამარ ჭაღიაშვილმა
კლასიკური მექანიკა კარგად აღწერს მცირე სიჩქარეების მქონე ინერციულ სისტემებში მიმდინარე ბუნებრივ პროცესებს, როგორიც არის დროითი და სივრცითი დამოკიდებულებები, სისტემებში მასისა და ენერგიის კავშირებს და ა.შ. მაგრამ მას არ აქვს ერთი გამაერთიანებელი თეორია, რომლის მიხედვითაც ბუნების სხვადასხვა ცნებები ერთმანეთთან არ არის დაკავშირებული. პუანკარემ გამოთქვა მოსაზრება, რომ ფიზიკის მოვლენები ნებისმიერ ათვლის ინერციულ სისტემაში თანაბარი ძალით უნდა მიმდინარეობდეს და არ არსებობს უპირატესი ათვლის სისტემები. არანაირი ექსპერიმენტი თუ თეორია არ იძლეოდა იმის საშუალებას, რომ გაგვერჩია ძირითადი და არაძირითადი ათვლის სისტემები. ამდენად, ნამდვილად საფიქრებელი იყო, რომ არა მხოლოდ მექანიკური, არამედ ყველა მოვლენა ბუნებაში ერთნაირად მიმდინარეობდა და ისინი არ უნდა შეცვლილიყვნენ ელექტრომაგნიტური პროცესებისთვისაც. კლარკ მაქსველს მიერ ჩამოყალიბებული ელექტრომაგნეტიზმის თეორის ერთ–ერთი მნიშვნელოვანი მიღწევა იყო ის, რომ მან შეაფასა სინათლის სიჩქარე c= 2.998*10^8m/s, მაგრამ თეორია ვერ ამბობდა, რომელ ათვლის სისტემაში ჰქონდა სინათლეს ეს კონკრეტული სიჩქარე. თუ სხვადასხვა ათვლის სისტემა სხვადასხვა სინათლის სიჩქარეს აღიქვამდა, მაშინ უნდა არსებულიყო უნივერსალური ათვლის სისტემა, სადაც სიჩქარე უნდა ყოფილიყო აბსოლუტური. პრობლემის გადასაჭრელად შემოიტანეს სპეციალური ათვლის სისტემის, ეთერის, რომელშიც სინათლეს მაქსველის მიერ შეფასებული სიჩქარით უნდა ემოძრავა. თეორიის შესამოწმებლად, ა. მაიკელსონმა და ე. მორლეიმ არაერთი ექსპერიმენტი ჩაატარეს. ისინი, ე.წ. მაიკელსონის ინტერფერომეტრის გამოყენებით ცდილობდნენ დაედგინათ დედამიწის ფარდობითი სიჩქარე ეთერთან მიმართებაში. ამისთვის ისინი ორი მიმართლებით პერპენდიკულარუალდ უშვებდნენ სინათლის სხივის კონას, რომლებიც სარკეზე უნდა არეკლილიყვნენ. სინათლის დეტექტირებისას განსხვავება ფარდობითი სიჩქარის დადგენის საშუალებას მისცემდათ. მათმა ექსპერიმენტმა შედეგი „ არ გამოიღო“ და სინათლის სხივების დეტექტირებას შორის განსხვავება არ იყო. ექსპერიმენტიდან ერთადერთი, ერთი შეხედვით, პარადოქსული დასკვნა გამომდინარეობდა, რომ თითოეული დამკვირვებელი ნებისმიერ ინერციულ სისტემაში სინათლეს ერთი და იგივე სიჩქარით აფიქსირებს. სინათლის სიჩქარე ასევე არ იყო დამოკიდებული იმაზე, გამომსხივებელი წყარო მოძრაობდა თუ გაჩერებული იყო. ექპერიმენტის შედეგად საჭირო გახდა შეექმნათ ახალი თეორია, რომელიც აღწერდა არა მხოლოდ კლასიკური მექანიკის კანონებს, არამედ ელექტრომაგნიტურ პროცესებსაც.
ალბერტ აინშტაინმა, 1905 წელს წამოაყენა მოსაზრება, რომ განეზოგადებინათ გალილეის გარდაქმნები ელექტრომაგნიტური პროცესებისთვისაც და დაყრდნობოდნენ მხოლოდ ემპირიულ მონაცემებს სინათლის ბუნების შესახებ. მონაცემების ანალიზის შედეგად შეიქმნა ფარდობითობის სპეციალური თეორია, რომელიც ორ პოსტულატს ემყარება:
- ყველა ინერციულ სისტემაში ფიზიკის კანონები ერთნაირად მოქმედებს;
- სინათლის სიჩქარე ერთი და იგივეა ნებისმიერ ათვლის ინერციულ სისტემაში და არ არის დამოკიდებული არც სინათლის წყაროს და არც ათვლის სისტემის მოძრაობაზე.
ფარდობითობის თეორია არის გალილეის ფარდობითობის პრინციპის განზოგადებული ვერსია, რომელიც ამბობს, რომ არა მხოლოდ მექანიკური პროცესები, არამედ ბუნების ყველა მოვლენა ერთნაირად მიმდინარეობს ყველა ინერციულ სისტემაში. სისტემის აღსაწერად, შესაბამისად საჭირო გახდა დამატებითი გარდაქმნების შემოტანა. ზღვრული სიჩქარე გარკვეულ სირთულეებს ქმნიდა ერთი ინერციული სისტემიდან მეორე სისტემაში გადასვლის აღწერაშიც: უნდა გარდაექმნათ კოორდინატები, რომელსაც ერთი დამკვირვებელი იყენებს მეორე დამკვირვებლის კოორდინატებად. ნიუტონის მექანიკაში ეს ადვილად ხდებოდა, რამდენადაც დროს აბსოლუტური გაგება ჰქონდა. ნიუტონის მექანიკაში, თუ ერთი ინერციული სისტემა მოძრაობდა მეორეს მიმართ გარკვეული სიჩქარით, ჩვენ უბრალოდ ამ სისტემის კონკრეტულ კოორტინატებს შორის სხვაობის შევკრებდით (გალილეის გარდაქმნები კოორდინატების მიმართ x ღერძის გასწვრივ x’= x + vt , y’ = y , z’ = z). ფარდობითობის პრინციპით კი ეს სიჩქარეების შეკრება პრობლემას ქმნიდა: თუ განვიხილავდით ორ ინერციულ სისტემას, რომლიდანაც ერთ–ერთი სინათლის სიჩქარით მოძრაობდა, მაშინ მათი ფარდობითი სიჩქარე სინათლის სიჩქარეზე მეტი გამოდიოდა, რაც რელატივისტური თეორიის მეორე კანონს ეწინააღმდეგებოდა. ფარდობითობის პრინციპის ჩამოყალიბებასთან ერთად საჭრო გახდა მკაცრად განესაზრვრათ მანამდე თითქოსდა გასაგები ცნებები, მაგალითად მოვნელათა ერთდროულობა და ა.შ.
სისტემის აღსაწერად, სადაც სინათლის სიჩქარე იყო ზღვრული სიჩქარე, საკმარისი არ იყო გალილეის გარდაქმნები მოხლოდ. აინშტაინმა თავისი თეორიის აღსაწერად შემოიტანა ჰოლანდიელი ფიზიკოსის ლორენცის გარდაქმნები.
ლორენცის გარდაქმნები სივრცისა და დროისთვის:
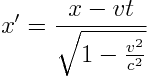
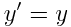 ,
, 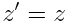
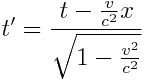
როდესაც სხეულები დაბალი სიჩქარეებით მოძრაობენ, მაშინ მოძრაობა გალილეის ფარდობითობის პრინციპით აღიწერება, მაგრამ სიჩქარის მატებასთან ერთად მათი სივრცული და დროითი დამოკიდებულებები იცვლება. ლორენცის გარდაქმნებმა ერთმანეთში აურია დროისა და სივრცის გაგება. თუ ერთი დამკვირვებლისთვის რაიმე იცვლბა სივრცეში, მეორე დამკვირვებლისთვის ეს შეიძლება დროში ცვლილებადაც იყოს აღქმული. ორი დამკვირვებლისთვის, რელატივისტურ მექანიკაში, ინფორმაცია მხოლოდ სივრცეში გადაადგილების ან მხოლოდ დროში ცვლილების შესახებ არასაკმარისია და სისტემის ბუნებას ვერ ახასიათებს. ამიტომ რელატივიზმში განიხილება არა მხოლოდ სივრცე განცალკევებულად ან დრო განცალკევებულად, არამედ დრო–სივრცე.
აინშტაინის ფარდობითობის თეორიას რამოდენიმე მნიშვნელოვანი შედეგი მოჰყვება:
- თუ რაიმე საგანი სინათლის სიჩქარესთან მიახლოებული სიჩქარით მოძრაობს, მაშინ მისი სიგრძე მცირდება. მაგალითად, თუ რაიმე L სიგრძის ჯოხის სიგრძე ნიუტონის მექანიკაში ორი კოორდინატს შორის მანძილით აღიწერებოდა
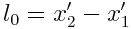
ფარდობითობის თეორიაში მისი სიგრძე დამოკიდებული გახდა მოძრაობის სიჩქარეზე
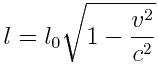
ფორმულიდან ვხედავთ, რომ სიჩქარის ზრდასთან ერთად მცირდება ჯოხის თავდაპირველი სიგრძეც.
- თუ ჯოხს მიმაგრებული ექნება საათი, მაშინ ვნახავთ, რომ c სიჩქარით მოძრავი სხეულისთვის დრო უფრო ნელა გადის, ვიდრე სხვა მატერიალური წერტილებისთვის.
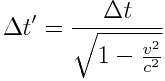
- გარდაქმნები გვიჩვენებს, რომ ზღვრული სიჩქარის შედეგად იცვლება სხეულის მასის აბსოლუტური გაგებაც:
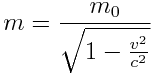
და შესაბამისად ენერგია მიიღებს შემდეგ სახეს:
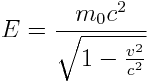
სხეულის მასასა და ენერგიას შორის კავშირი ფარდობითობის თეორიის ერთ–ერთი ყველაზე მნიშვნელოვანი დასკვნაა: სხეულის მასა და ენერგია ურთიერთშექცევადი სიდიდეებია, ანუ შესაძლებელია მასის ენერგიად გარდაქმნა და პირიქით, ენერგიის მასად გარდაქმნა. 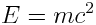 ფორმულის მიხედვით, ენერგა და მასა ერთმანეთის ტოლია ზღვრული სიჩქარის შემთხვევაში. რამდენადაც სინათლის სიჩქარე საკმაოდ დიდია, ადვილად შეგვიძლია დავინახოთ, რომ მცირე მასის შემთხვევაშიც კი საგანი დიდ ენერგიას იღებს. ამის მაგალითია ბირთვული იარაღი, რომელიც ბირთვის მასის მხოლოდ 1% იყენებს დამღუპველი ენერგიის მისაღებად. ეს დასკვნა იყო ერთ–ერთი ყველაზე რევოლუციური დასკვნა ფიზიკის სიტორიაში, რამდენადაც მანამდე ფიზიკაში მასა და ენერგია დამოუკიდებელ სუბსტანციებად განიხილებოდა.
ფორმულის მიხედვით, ენერგა და მასა ერთმანეთის ტოლია ზღვრული სიჩქარის შემთხვევაში. რამდენადაც სინათლის სიჩქარე საკმაოდ დიდია, ადვილად შეგვიძლია დავინახოთ, რომ მცირე მასის შემთხვევაშიც კი საგანი დიდ ენერგიას იღებს. ამის მაგალითია ბირთვული იარაღი, რომელიც ბირთვის მასის მხოლოდ 1% იყენებს დამღუპველი ენერგიის მისაღებად. ეს დასკვნა იყო ერთ–ერთი ყველაზე რევოლუციური დასკვნა ფიზიკის სიტორიაში, რამდენადაც მანამდე ფიზიკაში მასა და ენერგია დამოუკიდებელ სუბსტანციებად განიხილებოდა.
სივრცე–დროითი ერთიანობა სიახლე იყო ფილოსოფიური პრინციპების მიხედვით. ჩვენ ბუნებაში ვაკვირდებით ხდომილებებს, რომლებიც გარკვეული მანძილებითა და გარკვეული დროით არიან დაშორებულები და დროითი და სივრცითი დისტანციები არ იცვლება.
ფარდობითობის თეორიის გამცდარებას არაერთი ფიზიკოსი, მათემატიკოსი თუ ფილოსოფოსი შეეცადა. ისინი ამტკიცებდნენ, რომ ფარდობითობის თეორია მკაცრად მცნიერული ხასიათის არაა, არამედ საყრდენად აღებული აქვს ენერგიის, სივრცისა და დროის მეტაფიზიკური გაგება. კერძოდ, მას დროისა და სივრცის გაგებაში შემოაქვს ფარდობითობის ცნება, როგორც ბუნების კანონი, რაც დაშვებაა და არა ემპირიული დასკვნა. ფილოსოფიური არგუმენტების წარმომადგენლები ამბობენ, რომ მათემატიკური ფორმულირება შესაძლოა გამართული იყოს, მაგრამ თუ თავდაპირეველი პრინციპი არასწორია და ვერ არ აღწერს ბუნების კანონებს, მაშინ დანარჩენი გამოთვლებიც არასწორი იქნება. ფილოსოფოსები ამბობენ, რომ ფარდობითობის თეორია არ აღწერს ბუნების უზენაეს კანონებს, არამედ მას მხოლოდ კონკრეტული ლოკალური მნიშვნელობა აქვს. ფარდობითობის პრინციპს თითქოს შემოქვს ისეთი ცნება, რომელიც არ არის დამოკიდებული მდებარეობას, დროსა და სიჩქარეზე (სინათლის სიჩქარის ინვერიანტულობა) და თითქოს ამბობს, რომ ბუნების კანონები სამყაროს ნებისმიერ წერტილში ერთი და იგივეა, მაგრამ ის არ გვაძლევს სამყაროს ჭეშმარიტ ბუნებაზე ინფორმაციას.
მეორე არგუმენტი ფარდობითობის თეორიის წინააღმდეგ არის ენერგიისა და მატერიის დუალიზმის საკითხი. აინშტაინის ფორმულა, 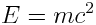 ინფორმაციას გვაძლევს მხოლოდ იმაზე, რომ მასას აქვს განუზომელი ენერგია, მაგრამ არაფერს ამბობს ჭეშმარიტი, წმინდა, ამოუწურავი და ყოვლისმომცველი ენერგიის ბუნების შესახებ. მტკიცება, რომ საგნის მასა გამრავლებული სინათლის სიჩქარის კვადრატზე ამ საგნის ენერგიაა, ანუ რომ საგნის ენერგია დამოკიდებულია ამ საგნის მასაზე, საშუალებას აღარ ტოვებს გავიგოთ მატერიისგან დამოუკიდებელი, წმინდა ენერგიის არსი. ფარდობითობის თეორიის ჩამოყალიბებამდე, მეცნიერები ფიქრობდნენ, რომ მატერია და ენერგია მუდმივია და არ იცვლება დროის განმავლობაში. არც მატერია და არც ენერგია არ წარმოიშობოდა და არ ნადგურდებოდა, ის ყოველთვის იყო და ყოველთვის იქნებოდა. ისინი ერთმანეთისგან დამოუკიდებლად არსებობდნენ. ფარდობითობის თეორიამ კი აჩვენა, რომ მატერია ენერგიის კიდევ ერთი ფორმაა და ის ენერგიისგან დამოუკიდებლად კი არ ინახება, არამედ ენერგიის კონსერვაცია მატერიის კონსერვაციასაც გულისხმობს.
ინფორმაციას გვაძლევს მხოლოდ იმაზე, რომ მასას აქვს განუზომელი ენერგია, მაგრამ არაფერს ამბობს ჭეშმარიტი, წმინდა, ამოუწურავი და ყოვლისმომცველი ენერგიის ბუნების შესახებ. მტკიცება, რომ საგნის მასა გამრავლებული სინათლის სიჩქარის კვადრატზე ამ საგნის ენერგიაა, ანუ რომ საგნის ენერგია დამოკიდებულია ამ საგნის მასაზე, საშუალებას აღარ ტოვებს გავიგოთ მატერიისგან დამოუკიდებელი, წმინდა ენერგიის არსი. ფარდობითობის თეორიის ჩამოყალიბებამდე, მეცნიერები ფიქრობდნენ, რომ მატერია და ენერგია მუდმივია და არ იცვლება დროის განმავლობაში. არც მატერია და არც ენერგია არ წარმოიშობოდა და არ ნადგურდებოდა, ის ყოველთვის იყო და ყოველთვის იქნებოდა. ისინი ერთმანეთისგან დამოუკიდებლად არსებობდნენ. ფარდობითობის თეორიამ კი აჩვენა, რომ მატერია ენერგიის კიდევ ერთი ფორმაა და ის ენერგიისგან დამოუკიდებლად კი არ ინახება, არამედ ენერგიის კონსერვაცია მატერიის კონსერვაციასაც გულისხმობს. 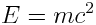 ფორმულა აჩვენებს, რომ მატერია შეიძლება წარმოიშვას გამოსხივების ენერგიის შედეგად და ასევე ის შეიძლება გაქრეს და გარდაიქმნას გამოსხივების ენერგიად. ფიზიკაში დუალიზმის მოხსნა არაერთხელ მომხდარა, ერთ–ერთი თვალსაჩინო მაგალითია მატერიისა და ძალის დუალიზმი ნიუტონის მექანიკაში. როგორც ვიცით, კლასიკურ მექანიკაში მატერიაა ის, რაზეც ძალა მოქმედებს, ან მატერია წარმოშობს ძალას (მაგ. გრავიტაცია). მატერია და ძალა სხეულებისთვის სხვადასხვა ასპექტებად განიხილებოდა, მაგრამ თანამედროვე ფიზიკაში ეს დუალიზმი მოხსნილია (ნაწილაკების ფიზიკა). ფარდობითობის თეორიის მოწინააღმდეგეები იშველიებენ რელიგიურ არგუმენტებს და ამბობენ, რომ აინშტაინი არ უშვებს არაფრისგან წარმოშობის ფაქტს. ისინი თანხმდებიან, რომ როგორც სინათლეს აქვს ტალღური და კორპუსკულური ბუნება ასეთივეა მასისა და ენერგიის დამოკიდებულებაც, მაგრამ მასისა და ენერგიის ეკვივალენტობა, რასაც ფორმულა აღწერს, მათემატიკური ფიქციაა და არ აღწერს რეალობას. აინშტაინი არ ეძებდა აბსოლუტურ ჭეშმარიტებას, რამდენადაც ის განზოგადების თეორიაშიც პარადიგმად მუდმივ ცვალებად ობიექტს იღებდა და არა უცვლელს.
ფორმულა აჩვენებს, რომ მატერია შეიძლება წარმოიშვას გამოსხივების ენერგიის შედეგად და ასევე ის შეიძლება გაქრეს და გარდაიქმნას გამოსხივების ენერგიად. ფიზიკაში დუალიზმის მოხსნა არაერთხელ მომხდარა, ერთ–ერთი თვალსაჩინო მაგალითია მატერიისა და ძალის დუალიზმი ნიუტონის მექანიკაში. როგორც ვიცით, კლასიკურ მექანიკაში მატერიაა ის, რაზეც ძალა მოქმედებს, ან მატერია წარმოშობს ძალას (მაგ. გრავიტაცია). მატერია და ძალა სხეულებისთვის სხვადასხვა ასპექტებად განიხილებოდა, მაგრამ თანამედროვე ფიზიკაში ეს დუალიზმი მოხსნილია (ნაწილაკების ფიზიკა). ფარდობითობის თეორიის მოწინააღმდეგეები იშველიებენ რელიგიურ არგუმენტებს და ამბობენ, რომ აინშტაინი არ უშვებს არაფრისგან წარმოშობის ფაქტს. ისინი თანხმდებიან, რომ როგორც სინათლეს აქვს ტალღური და კორპუსკულური ბუნება ასეთივეა მასისა და ენერგიის დამოკიდებულებაც, მაგრამ მასისა და ენერგიის ეკვივალენტობა, რასაც ფორმულა აღწერს, მათემატიკური ფიქციაა და არ აღწერს რეალობას. აინშტაინი არ ეძებდა აბსოლუტურ ჭეშმარიტებას, რამდენადაც ის განზოგადების თეორიაშიც პარადიგმად მუდმივ ცვალებად ობიექტს იღებდა და არა უცვლელს.
თანამედროვე ფიზიკისა და კოსმოლოგიის ისეთი ფუნდამენტური თეორიები, როგორიცაა ნაწილაკების ფიზიკა, სამყაროს სტანდარტული მოდელი და ა.შ. დამყარებულია ფარდობითობის თეორიის პრინციპებზე. თეორია, ასევე, შემოწმებულია არაერთი ექსპერიმენტის მეშვეობით, მათ შორის აღსანიშნავია დიდი ადრონული ამაჩქარებელი CERN-ში, ამიტომ დღეს თავისუფლად შეიძლება ითქვას, რომ ფარდობითობის პრინციპი კარგად აღწერს სამყაროს იმ ნაწილს, სადაც კლასიკური მექანიკის, ელექტრომაგნეტიზმისა და ნაწილაკების ფიზიკა მოქმედებს.
მიუხედავად იმისა, რომ ფარდობითობის პრინციპის არაერთი მტკიცებულება არსებობს, მეცნიერების ნაწილი მის აბსოლუტურობას კითხვის ნიშნის ქვეშ აყენებს; იმ შემთხვევისთვის, თუ სინათლის სიჩქარე არ არის ბუნების მუდმივა ათვლის ნებისმიერ სისტემაში, არამედ ის სხვადასხვა მდგომარეობაში იცვლის მნიშვნელობას, რა ბედი ეწევა დღემდე არსებულ თეორიებს? მაგრამ ჯერ–ჯერობით არც ექპერიმენტულად და არც მათემატიკურად არ მტკიცდება სინათლის სიჩქარის ცვალებადობა გარემოს მიხედვით. რამდენადაც ბუნებაში ერთადერთი უცვლელია ის, რომ ყველაფერი იცვლება, სავარაუდოა, რომ დროთა განმავლობაში დიდი გაერთიანების თეორიის საფუძვლებიც იქნება აღმოჩენილი, ან ის განყენებული პრინციპები, რასაც ფილოსოფოსები ასე აქტიურად ეძებენ ბუნების კანონებში.