ამოცანა 1.1
მატერიალური წერტილის სიჩქარე დეკარტის კოორდინატთა სისტემაში მის მდებარეობაზე შემდეგნაირად არის დამოკიდებული: \(\vec{v}=c\vec{i}+bx\vec{j}\) ,სადაც c და b – დადებითი მუდმივი სიდიდეებია. დროის საწყის მომენტში მატერიალური წერტილის რადიუს-ვექტორი ნულის ტოლია: r(0) = 0 .
განვსაზღვროთ:
а) მოძრაობის კანონები \(\vec{r}\left ( t \right )\), \(\vec{v}\left ( t \right )\) სიჩქარისა და \(\vec{a}\left ( t \right )\) აჩქარების ცვლილებები, აჩქარების \(a_{\tau }\) ტანგენციალური და \(a_{n }\) ნორმალური მდგენელები;
б) მატერიალური წერტილის ტრაექტორიის განტოლება y(x);
в) ტრაექტორიის სიმრუდის რადიუსი ρ (t) ;
г) \(\vec{v}\left ( t \right )\) სიჩქარესა და \(\vec{a}\left ( t \right )\) აჩქარებას შორის კუთხე \(\varphi \left ( t \right )\).
ამოცანა 1.2
დედამიწის ზედაპირიდან H სიმაღლეზე მყოფი სხეული გაისროლეს ჰორიზონტალურად \(v_{0}\) საწყისი სიჩქარით. განვსაზღვროთ სხეულის მოძრაობის კანონი, ტრაექტორიის განტოლება, სიჩქარისა და აჩქარების ცვლილებების კანონები, აჩქარების ტანგენციური და ნორმალური მდგენელები, ასევე ტრაექტორიის სიმრუდის რადიუსი დროის ნებისმიერ მომენტში.
ამოცანა 1.3
ნავი კვეთს მდინარეს მდინარის მიმართ მუდმივი \(\vec{v}_{n}\) სიჩქარით, რომელიც მდინარის დინების სიჩქარის პერპენდიკულარულია. d განის მქონე მდინარის დინების მოდული პარაბოლური კანონით იზრდება ნაპირებიდან მდინარის შუისკენ 0 მნიშვნელობიდან \(\vec{v}_{m}\) მნიშვნელობამდე. ვიპოვნოთ ნავის ტრაექტორიის განტოლება, მისი მოძრაობის \(\tau\) დრო, ასევე ნავის \(l\) დინების მიმართულებით წატაცება ნაპირიდან შეცურვის ადგილიდან საპირისპირო ნაპირზე მიყუდების ადგილამდე.
ამოცანა 1.4
განვსაზღვროთ \(\vec{v}_{1}\) სიჩქარით მოძრავი ტრამვაის გვერდითა მინაზე წვიმის წვეთების ტრაექტორიის ფორმა, როცა ტრამვაი ამუხრუჭებს \(\vec{a}\) აჩქარებით. წვიმის წვეთები ეშვება ვერტიკალურად ქვევით მიწისადმი მუდმივი \(\vec{v}_{2}\) სიჩქარით.
ამოცანა 1.5
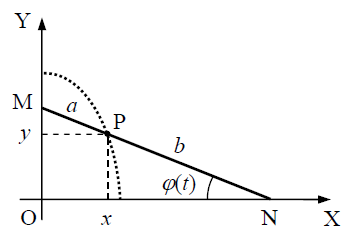
მყარი MN ძელაკის ბოლოები თავისუფლად სრიალებენ MON კუთხის გვერდებზე. ვიპოვნოთ ძელაკის იმ P წერტილის ტრაექტორია, რომელიც მას ყოფს а და b სიგრძეების მქონე ნაწილებად.
ამოცანა 1.6
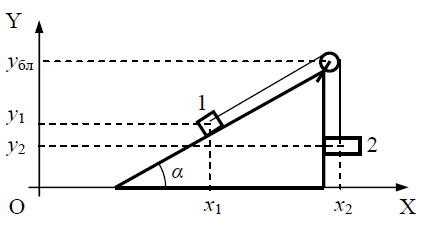
ამოცანა 1.7
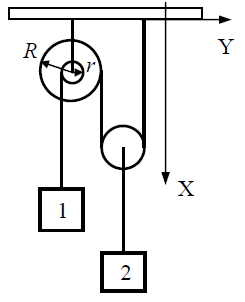
ამოცანა 1.8
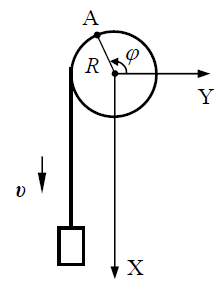
ამოცანა 1.9
ამოცანა 1.10
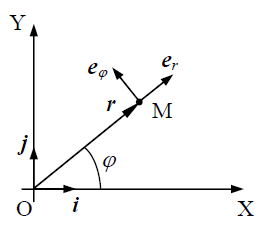
მატერიალური წერტილის მოძრაობა პოლარულ კოორდინატთა სისტემაში მოცემულია პოლარული კოორდინატების შემდეგი ურთიერთკავშირით \(r\left ( \varphi \right )=2a\left ( 1+\cos \varphi \right )\), ამასთან პოლარული კუთხე იზრდება წრფივად დროში \(\varphi \left ( t \right )=bt\). განვსაზღვროთ სიჩქარისა და აჩქარების მოდულების დამოკიდებულება დროზე.
ამოცანა 1.11
პლანეტა მოძრაობს მზის ირგვლივ კეპლერის კანონების შესაბამისად ელიფსურ ტრაექტორიაზე \(r\left ( 1-e\cos \varphi \right )=\rho\) . ელიფსის პარამეტრი \(\rho\), ექსცენტრისიტეტი \(e\) და სექტორული სიჩქარე \(\sigma\) ჩავთვალოთ მოცემულად. განვსაზღვროთ პლანეტის აჩქარების მდგენელების დამოკიდებულება \(r\) და \(\varphi\) პოლარული სისტემის კოორდინატებზე.
ამოცანა 1.12
R რადიუსის მქონე ვერტიკალურ ღრუ ცილინდრში მოძრაობს მცირე ზომის სხეული. დროის საწყის მომენტში სხეულის სიჩქარე პერპენდიკულარულია ცილინდრის ღერძისა და უდრის \(v_{0}\)-ს. განვსაზღვროთ მატერიალური წერტილის სიჩქარისა და აჩქარების ცვლილებების კანონები ცილინდრულ კოორდინატთა სისტემაში, ასევე სიჩქარესა და აჩქარებას შორის α(t) კუთხე.
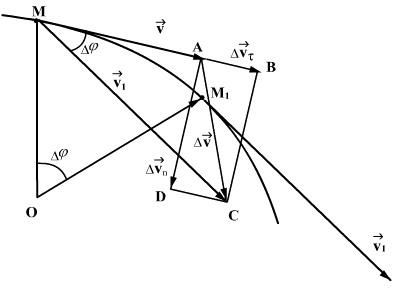
წრფივი მოძრაობისას სიჩქარისა და აჩქარების ვექტორები ემთხვევა ტრაექტორიის მიმართულებას. განვიხილოთ მატერიალური წერტილის ბრტყელი მრუდწირული მოძრაობა. ტრაექტორიის ნებისმიერ წერტილში სიჩქარის ვექტორი მიმართულია ტრაექტორიის მხების გასწვრივ. დავუშვათ, რომ ტრაექტორიის М წერტილში სიჩქარე იყო 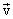 , ხოლო.М1 წერტილში გახდა
, ხოლო.М1 წერტილში გახდა 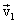 . ამასთან ვთვლით, რომ М წერტ М1 წერტლიში გადასვლის დროის მონაკვეაათი იმდენად მცირეა, რომ აჩქარების სიდიდისა და მიმართულების ცვლილება შეიძლება უგულებელვყოთ. იმისათვის რათა მოვძებნოთ
. ამასთან ვთვლით, რომ М წერტ М1 წერტლიში გადასვლის დროის მონაკვეაათი იმდენად მცირეა, რომ აჩქარების სიდიდისა და მიმართულების ცვლილება შეიძლება უგულებელვყოთ. იმისათვის რათა მოვძებნოთ 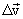 სიჩქარის ცვლილება, აუცილებელია განვსაზღვროთ ვექტორული სხვაობა:
სიჩქარის ცვლილება, აუცილებელია განვსაზღვროთ ვექტორული სხვაობა:
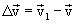
ამისათვის გადავიტანოთ 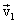 თავის თავის პარალელურად ისე, რომ მისი სათავე დავამთხვიოთ М წერტილს. ორი ვექტორის სხვაობა ტოლია
თავის თავის პარალელურად ისე, რომ მისი სათავე დავამთხვიოთ М წერტილს. ორი ვექტორის სხვაობა ტოლია 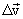 ვექტორისა, რომელიც აერთებს მათ ბოლოებს და ტოლია სიჩქარეებზე როგორც გვერდებზე აგებული МАС სამკუთხედის АС გვერდისა. დავშალოთ
ვექტორისა, რომელიც აერთებს მათ ბოლოებს და ტოლია სიჩქარეებზე როგორც გვერდებზე აგებული МАС სამკუთხედის АС გვერდისა. დავშალოთ 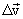 ვექტორი ორ მდგენელად АВ АD, და აღვნიშნოთ ისინი შესაბამისად
ვექტორი ორ მდგენელად АВ АD, და აღვნიშნოთ ისინი შესაბამისად 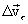 და
და 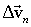 . ამდაგვარად სიჩქარის ცვლილების ვექტორი
. ამდაგვარად სიჩქარის ცვლილების ვექტორი 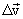 ტოლია ორი ვექტორის ვექტორული ჯამისა:
ტოლია ორი ვექტორის ვექტორული ჯამისა:
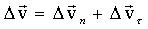
განსაზღვრების თანახმად:
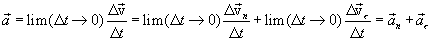 |
(1.15) |
ტანგენციური აჩქარება 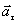 ახასიათებს მოძრაობის სიჩქარის რიცხვითი მნიშვნელობის ცვლილების სისწრაფეს და მიმართულია ტრაექტორიის მხების გასწვრივ.
ახასიათებს მოძრაობის სიჩქარის რიცხვითი მნიშვნელობის ცვლილების სისწრაფეს და მიმართულია ტრაექტორიის მხების გასწვრივ.
შესაბამისად
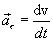 |
(1.16) |
ნორმალური აჩქარება 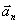 ახასიათებს სიჩქარის მიმართულების ცვლილების სისწრაფეს. გამოვთვალოთ ვექტორი:
ახასიათებს სიჩქარის მიმართულების ცვლილების სისწრაფეს. გამოვთვალოთ ვექტორი:
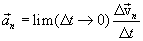
ამისთვის М და М1 წერტილებში ტრაექტორიის მხებების მიმართ გავავლოთ პერპენდიკულარები. გადაკვეთის წერტილი აღვნიშნოთ О-თი. საკმაოდ მცირე 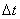 -სთვის მრუდწირული ტრაექტორიის უბანი R რადიუსიანი წრეწირის ნაწილად შეიძლება ჩაითვალოს. სამკუთხედები МОМ1 და МВС მსგავსებია, რადგან წარმოადგენენ ტოლფერდა სამკუთხედებს, რომელთაც წვერის კუთხეები ტოლი აქვთ. ამიტომ:
-სთვის მრუდწირული ტრაექტორიის უბანი R რადიუსიანი წრეწირის ნაწილად შეიძლება ჩაითვალოს. სამკუთხედები МОМ1 და МВС მსგავსებია, რადგან წარმოადგენენ ტოლფერდა სამკუთხედებს, რომელთაც წვერის კუთხეები ტოლი აქვთ. ამიტომ:
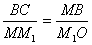
ანუ
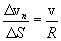
მაგრამ 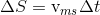 , მაშინ:
, მაშინ:
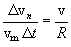
გადავიდეთ ზღვარზე როცა 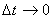 და გავითვალისწინოთ, რომ ამ დროს vm=v, ვიპოვით:
და გავითვალისწინოთ, რომ ამ დროს vm=v, ვიპოვით:
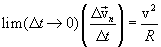 ,
,
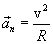 |
(1.17) |
რადგან როცა 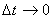 მაშინ კუთხე
მაშინ კუთხე 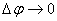 , ამ აჩქარების მიმართულება ემთხვევა
, ამ აჩქარების მიმართულება ემთხვევა 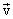 სიჩქარის ნორმალის მიმართულებას, ანუ აჩქარების ვექტორი
სიჩქარის ნორმალის მიმართულებას, ანუ აჩქარების ვექტორი 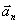 პერპენდიკულარულია სიჩქარის
პერპენდიკულარულია სიჩქარის 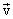 . ამიტომ ამ აჩქარებას ხშირად უწოდებენ ცენტრისკენულს. R-ს უწოდებენ სიმრუდის რადიუსს.
. ამიტომ ამ აჩქარებას ხშირად უწოდებენ ცენტრისკენულს. R-ს უწოდებენ სიმრუდის რადიუსს.
სრული აჩქარება განისაზღვრება ტანგენციალური და ნორმალური მდგენელების ვექტორული ჯამით (1.15). რადგან ამ აჩქარებების ვექტორები ურთიერთპერპენდიკულარულია, ამიტომ სრული აჩქარების მოდული იქნება:
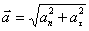 |
(1.18) |
სრული აჩქარების მიმართულება (კუთხე ტრაექტორიის მხებთან) განისაზღვრება 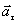 და
და 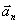 ვექტორების სიდიდეების ფარდობით:
ვექტორების სიდიდეების ფარდობით:
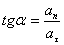
კინემატიკაში შეიძლება გამოიყოს ოთხი ძირითადი ტიპის ამოცანა:
1. კინემატიკის ზოგადი პირდაპირი ამოცანა:
რადიუს-ვექტორის დროზე ცნობილი დამოკიდებულებით საჭიროა განისაზღვროს სიჩქარისა და აჩქარების ვექტორები და მათი მოდულები v და а, აჩქარების ნორმალური და ტანგენციური მდგენელები, ტრაექტორიის სიმრუდის რადიუსი R.
2. კინემატიკის ზოგადი შებრუნებული ამოცანა:
სიჩქარის ან აჩქარების ცნობილი ვექტორებით საჭიროა ტრაექტორიის სახის აღდგენა, ანუ რადიუს-ვექტორის მოძებნა, ხოლო შემდეგ ყველა დანარჩენი პარამეტრების მოძებნა, რაც მითითებულია პუნქტ 1-ში.
3. კინემატიკის კერძო პირდაპირი ამოცანა:
გზის დროზე ცნობილი დამოკიდებულებით საჭიროა მოიძებნოს სხეულის სიჩქარე და აჩქარება. ამ შემთხვევაში შესაძლებელია მხოლოდ სიჩქარისა და აჩქარების მოდულების მოძებნა:
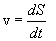 და
და 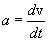 .
.
ვექტორები 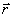 ,
,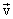 ,
, 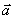 , ასევე
, ასევე 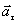 და
და 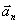 ამ ამოცანებში ვერ მოიძებნება.
ამ ამოცანებში ვერ მოიძებნება.
4. კინემატიკის კერძო შებრუნებული ამოცანა:
სიჩქარის ან აჩქარების ცნობილი დროზე დამოკიდებულებით საჭიროა აღვადგინოთ გზის დროზე დამოკიდებულება:
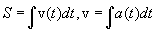
აჩქარება ახასიათებს სიჩქარის ცვლილების სისწრაფეს, ანუ სიჩქარის სიდიდის ცვლილებას დროის ერთეულში.
საშუალო აჩქარების ვექტორი. სიჩქარის 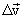 ნაზრდის ფარდობა დროის
ნაზრდის ფარდობა დროის 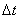 , შუალედთან, რომელშიც წარმოიქმნა ეს ნაზრდი, გამოსახავს საშუალო აჩქარებას:
, შუალედთან, რომელშიც წარმოიქმნა ეს ნაზრდი, გამოსახავს საშუალო აჩქარებას:
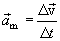
საშუალო აჩქარების ვექტორი მიმართულებით ემთხვევა 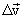 ვექტორს.
ვექტორს.
აჩქარება, ანუ მყისი აჩქარება ტოლია საშუალო აჩქარების ზღვრისა როცა 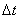 დროის შუალედი მიისწრაფის ნულისკენ:
დროის შუალედი მიისწრაფის ნულისკენ:
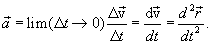 |
(1.13) |
კოორდინატთა შესაბამის ღერძებზე პროექციებით წარმოვადგენთ ასე:
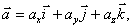
ანუ
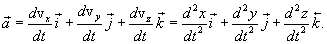 |
(1.14) |