მატერიალური წერტილის მოძრაობის დასახასიათებლად შემოაქვთ ვექტორული ფიზიკური სიდიდე - სიჩქარე, რომელიც განსაზღვრავს როგორც მოძრაობის სისწრაფეს, ასევე მის მიმართულებას მოცემულ მომენტში.
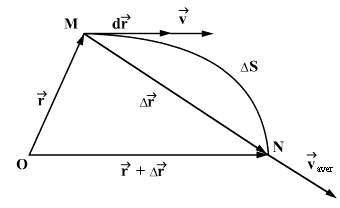
ვთქვათ მატერიალური წერტილი მოძრაობს МN მრუდწირულ ტრაექტორიაზე ისე, რომ t დროის მომენტში იმყოფება.М წერტილში, ხოლო დროის 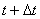 მომენტში N წერტილში. М და N წერტილების რადიუს-ვექტორები შესაბამისად არის
მომენტში N წერტილში. М და N წერტილების რადიუს-ვექტორები შესაბამისად არის 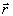 და
და 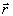 +
+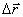 ხოლო МN რკალის სიგრძე არის
ხოლო МN რკალის სიგრძე არის 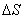 (ნახ. 1.3).
(ნახ. 1.3).
წერტლის საშუალო სიჩქარის ვექტორი vm t -დან 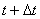 -მდე დროის ინტერვალში ეწოდება ამ ინტერვალში რადიუს ვექტორის
-მდე დროის ინტერვალში ეწოდება ამ ინტერვალში რადიუს ვექტორის 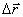 ნაზრდის ფარდობას ამ დროის ინტერვალის
ნაზრდის ფარდობას ამ დროის ინტერვალის 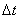 სიდიდესთან:
სიდიდესთან:
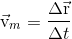 |
(1.5) |
საშუალო სიჩქარის ვექტორი მიმართულია ისევე, როგორც გადაადგილების ვექტორი 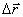 ანუ МN ქორდის გასწვრივ.
ანუ МN ქორდის გასწვრივ.
მყისი სიჩქარე ან სიჩქარე მოცემულ მომენტში. თუ გამოსახულებაში (1.5) გადავალთ ზღვარზე, მივასწრაფებთ რა 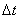 -ს ნულისკენ, მაშინ მატერიალური წერტილის მოცემულ t მომენტში ტრაექტორიის М წერტილის გავლის სიჩქარის ვექტორის გამოსახულებას მივიღებთ.
-ს ნულისკენ, მაშინ მატერიალური წერტილის მოცემულ t მომენტში ტრაექტორიის М წერტილის გავლის სიჩქარის ვექტორის გამოსახულებას მივიღებთ.
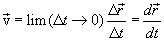 |
(1.6) |
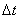 - სიდიდის შემცირების პროცესში წერტილი N უახლოვდება М წერტილს და ქორდა МN, შემობრუნდება რა М წერტილის ირგვლივ, ზღვარში მიმართულებით დაემთხვევა М წერტილში ტრაექტორიის მხების გასწვრივ მიმართულებას. ამიტომ ვექტორი
- სიდიდის შემცირების პროცესში წერტილი N უახლოვდება М წერტილს და ქორდა МN, შემობრუნდება რა М წერტილის ირგვლივ, ზღვარში მიმართულებით დაემთხვევა М წერტილში ტრაექტორიის მხების გასწვრივ მიმართულებას. ამიტომ ვექტორი 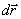 და მოძრავი წერტილის სიჩქარე v მიმართულია ტრაექტორიის მხების გასწვრივ მოძრაობის მიმართულებით. მატერიალური წერტილის მოძრაობის სიჩქარის ვექტორი v შეიძლება დავშალოთ სამ მდგენელად დეკარტის კოორდინათა ღერძების მიმართულებით.
და მოძრავი წერტილის სიჩქარე v მიმართულია ტრაექტორიის მხების გასწვრივ მოძრაობის მიმართულებით. მატერიალური წერტილის მოძრაობის სიჩქარის ვექტორი v შეიძლება დავშალოთ სამ მდგენელად დეკარტის კოორდინათა ღერძების მიმართულებით.
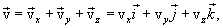 |
(1.7) |
სადაც 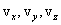 - სიჩქარის ვექტორის მდგენელებია х, у, z კოორდინატთა ხერძებზე.
- სიჩქარის ვექტორის მდგენელებია х, у, z კოორდინატთა ხერძებზე.
თუ (1.6)-ში ჩავსვამთ მატერიალური წერტილის რადიუს-ვექტორის მნიშვნელობებს (1.1)-დან და ჩავატარებთ წევრობრივ დიფერენცირებას, მივიღებთ:
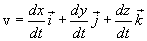 |
(1.8) |
(1.7) და (1.8) განტოლებების შედარებით ვღებულობთ, რომ მატერიალური წერტილის სიჩქარის პროექციები მართკუთხა დეკარტის კოორდინატთა სისტემის ღერძებზე წერტილის შესაბამისი კოოედინატების დროით პირველი წარმოებულების ტოლია:
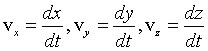 |
(1.9) |
ამიტომ სიჩქარის რიცხვითი მნიშვნელობა არის შემდეგი:
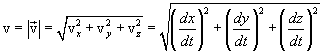 |
(1.10) |
მოძრაობას, რომლის დროსაც მატერიალური წერტილის სიჩქარის მიმართულება არ იცვლება, წრფივი ეწოდება. თუ წერტილის მყისი სიჩქარის რიცხვითი მნიშვნელობა მოძრაობის დროს რჩება უცვლელი, ასეთ მოძრაობას თანაბარი ეწოდება.
თუ ნებისმიერ დროის ტოლ შუალედებში წერტილი გადის სხვადასხვა სიგრძის გზებს, მაშინ რიცხვითი მნიშვნელობა მისი მყისი სიჩქარისა დროში იცვლება. ასეთ მოძრაობას უწოდებენ არათანაბარს.
ამ შემთხვევაში ხშირად იყენებენ vm სკალარულ სიდიდეს, რომელსაც არათანაბარი მოძრაობის საშუალო გზიურ სიჩქარეს უწოდებენ ტრაექტორიის მოცემულ 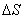 უბანზე. იგი ტოლია ისეთი თანაბარი მოძრაობის სიჩქარის რიცხვითი მნიშვნელობისა, რომლის დროსაც
უბანზე. იგი ტოლია ისეთი თანაბარი მოძრაობის სიჩქარის რიცხვითი მნიშვნელობისა, რომლის დროსაც 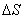 მანძილის გავლაზე იხარჯება იგივე
მანძილის გავლაზე იხარჯება იგივე 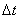 დრო რაც მოცემული არათანაბარი მოძრაობისას:
დრო რაც მოცემული არათანაბარი მოძრაობისას:
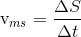 |
(1.11) |
სიჩქარეთა შეკრების კანონი. თუ მატერიალური წერტილი ერთდროულად მონაწილეობს რამდენიმე მოძრაობაში, მაშინ მარეზულტირებელი გადაადგილება 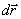 დამოუკიდებელი მოძრაობის კანონის შესაბამისად, უდრის თითოეული ამ მოძრაობით გამოწვეული ელემენტური გადაადგილებების ვექტორულ (გეომეტრიულ) ჯამს:
დამოუკიდებელი მოძრაობის კანონის შესაბამისად, უდრის თითოეული ამ მოძრაობით გამოწვეული ელემენტური გადაადგილებების ვექტორულ (გეომეტრიულ) ჯამს:
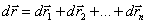
(1.6) განსაზღვრების შესაბამისად:
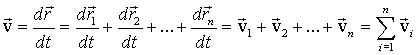 |
(1.12) |
ასე რომ, მარეზულტირებელი მოძრაობის სიჩქარე 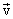 ტოლია ყველა იმ მოძრაობათა სიჩქარეების გეომეტრიული ჯამისა, რომლებშიც ღებულობს მონაწილეობას მატერიალური წერტილი, (ეს არის სიჩქარეთა შეკრების კანონი).
ტოლია ყველა იმ მოძრაობათა სიჩქარეების გეომეტრიული ჯამისა, რომლებშიც ღებულობს მონაწილეობას მატერიალური წერტილი, (ეს არის სიჩქარეთა შეკრების კანონი).
მატერიალური წერტილის გადაადგილების ვექტორი
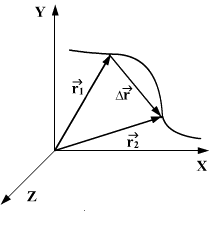
t1-დან t2 დროის შუალედში ანუ წერტილის რადიუს-ვექტორის ნაზრდი განსახილველ დროის შუალედში არის
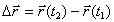 |
(1.4) |
წრფივი მოძრაობისას გადაადგილების ვექტორი ემთხვევა ტრაექტორიის შესაბამის უბანს. რადგან გადაადგილება არის ვექტორი, ამიტომ ადგილი აქვს მოძრაობათა დამოუკიდებლობის კანონს: თუ მატერიალური წერტილი მონაწილეობას იღებს რამდენიმე მოძრაობაში, მაშინ წერტილის შედეგი გადაადგილება იმავე დროის შუალედში ცალ-ცალკე თითოეული მოძრაობით შესრულებული გადაადგილებების ვექტორული ჯამის ტოლია.
მატერიალური წერტილის ტრაექტორია ეწოდება წირს, რომელსაც მოძრაობისას ეს წერტილი შემოწერს. ტრაექტორიის ფორმის მიხედვით განარჩევენ წერტილის წრფივ და მრუდწირულ მოძრაობებს. თუ წერტილის ტრაექტორიის ყველა უბანი ძევს ერთ სიბრტყეში, მაშინ წერტილის მოძრაობა არის ბრტყელი.
განტოლებები (1.2) და (1.3) იძლევიან წერტილის ტრაექტორიას ე.წ. პარამეტრული ფორმით. პარამეტრის როლს ასრულებს t დრო. თუ ამ განტოლებებეს ერთობლივად ამოვხსნით t დროის გამორიცხვით, ვიპოვნით ტრაექტორიის განტოლებას.
გზის სიგრძე. მატერიალური წერტილის S გზის სიგრძე ეწოდება განსახილველ დროის შუალედში წერტილის მიერ განვლილი ტრაექტორიის ყველა უბნის სიგრძეთა ჯამს.
М მატერიალური წერტილის მოძრაობისას მისი კოორდინატები x,y,z და რადიუს-ვექტორი 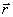 იცვლება t დროის განმავლობაში.
იცვლება t დროის განმავლობაში.
ამიტომ მატერიალური წერტილის მოძრაობის კანონის მოსაცემად აუცილებელია მივუთითოთ ან სამივე კოორდინატის დროზე ფუნქციური დამოკიდებულების სახე:
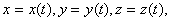 |
(1.2) |
ან რადიუს-ვექტორის დროზე დამოკიდებულება
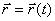 |
(1.3) |
სამ სკალარულ განტოლებას (1.2) ან ერთ მათ ექვივალენტურ ვექტორულ განტოლებას (1.3) ეწოდება მატერიალური წერტილის კინემატიკური განტოლებები.


