გამოვიყენოთ განტოლება:
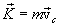 და
და 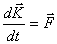 ,
,
შეგვიძლია ჩავწეროთ
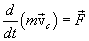
ანუ
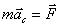 |
(3.12) |
ამდენად, მექანიკური სისტემის ინერციის ცენტრი მოძრაობს როგორც მატერიალური წერტილი, რომლის მასა ტოლია მთელი სისტემის მასისა და რომელზეც მოქმედებს ძალა, რომელიც ტოლია სისტემაზე მოდებული გარეშე ძალების მთავარი ვექტორისა. ზოგადად მყარი სხეულის მოძრაობა შეიძლება განვიხილოთ როგორც ჯამი ორი მოძრაობისა: გადატანითი სიჩქარით  , რომელიც ტოლია ცხეულის ინერციის ცენტრის
, რომელიც ტოლია ცხეულის ინერციის ცენტრის 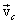 სიჩქარისა, და ინერციის ცენტრის ირგვლივ ბრუნვა. ამიტომ უკანასკნელ განტოლებას ხშირად უწოდებენ მყარი სხეულის გადატანითი მოძრაობის დინამიკის ძირითად განტოლებას.
სიჩქარისა, და ინერციის ცენტრის ირგვლივ ბრუნვა. ამიტომ უკანასკნელ განტოლებას ხშირად უწოდებენ მყარი სხეულის გადატანითი მოძრაობის დინამიკის ძირითად განტოლებას.
თუ გამოვიყენოთ იმპულსის გამოსახულებას
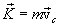
და ნიუტონის მეორე კანონს, შეიძლება ჩავწეროთ
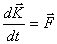 |
(3.11) |
სადაც 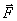 არის სხეულზე მოქმედი ყველა გარე ძალის ტოლქმედი.
არის სხეულზე მოქმედი ყველა გარე ძალის ტოლქმედი.
უკანასკნელი განტოლება არის ნებისმიერ მექანიკურ სისტემაზე იმპულსის განტოლების განზოგადება, რადგან მისი წარმოდგენა ყოველთვის შეიძლება ისეთი მატერიალური წერტილების სისტემად, რომლებიც ურთიერთქმედებენ ერთმანეთთან და გარეშე სხეულებთან. გარეშე სხეულები ეწოდება სხეულებს, რომლებიც არ შედიან განსახილველი სისტემის შემადგენლობაში, ხოლო ძალებს, რომლებიც ამ სხეულებისგან მოქმედებს სისტემაზე, ეწოდებათ გარეშე ძალები. შესაბამისად, ძალებს, რომლითაც ურთიერთქმედებენ მატერიალური წერტილები, რომლებიც ეკუთვნის მოცემულ სისტემას, ეწოდება შიდა ძალები და მათი ტოლქმედი ტოლია ნულის. განტოლება (3.11) აჩვენებს, რომ მექანიკური სისტემის იმპულსის ცვლილების სიჩქარე ტოლია სისტემაზე მოქმედი ყველა გარეშე ძალის მთავარი ვექტორისა (ტოლქმედისა).
ადრე განხილულ ნიუტონის კანონებში იგულისხმებოდა, რომ სხეულს აქვს იმდენად მცირე ზომები, რომ შეიძლება მისი წარმოდგენა მატერიალურ წერტილად. ნებისმიერი არადეფორმირებადი სხეულის მოძრაობა შეიძლება აღიწეროს (3.6)-ის ანალოგიური განტოლებით. თუ სხეული შედგება n მატერიალური წერტილებისგან მასებით 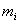 და რადიუს-ვექტორებით
და რადიუს-ვექტორებით 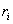 , მაშინ მატერიალური წერტილების სისტემის მასათა ცენტრი ეწოდება სისტემის ისეთ წერტილს, რომლის რადიუს-ვექტორიც განისაზღვრება შემდეგნაირად:
, მაშინ მატერიალური წერტილების სისტემის მასათა ცენტრი ეწოდება სისტემის ისეთ წერტილს, რომლის რადიუს-ვექტორიც განისაზღვრება შემდეგნაირად:
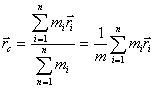 |
(3.7) |
სადაც 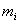 და
და 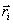 არის სისტემის i-ური წერტილის მასა და რადიუს-ვექტორი, შესაბამისად ხოლო m - სისტემის სრული მასა.
არის სისტემის i-ური წერტილის მასა და რადიუს-ვექტორი, შესაბამისად ხოლო m - სისტემის სრული მასა.
შესაბამისად ცენტრისა და სისტემის ყველა წერტილის დეკარტის კოორდინატებს შორის დამოკიდებულება არის ასეთი:
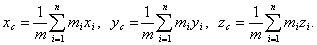
ინერციის ცენტრის სიჩქარეა:
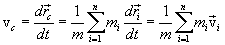 |
(3.8) |
სისტემის იმპულსი. სისტემის ყველა მატერიალური წერტილის იმპულსთა გეომეტრიულ ჯამს უწოდებენ სისტემის იმპულსს და აღნიშნავენ 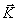 -თი:
-თი:
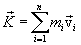 ,
,
მაშინ მასათა ცენტრის სიჩქარე იქნება
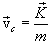 |
(3.9) |
ამდენად, (3.9)-დან გამოდის, რომ სისტემის იმპულსი ტოლია მთელი სისტემის მასის ნამრავლისა მისი მასათა ცენტრის სიჩქარეზე:
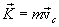 |
(3.10) |
ნიუტონის კანონი ძეიძლება ჩაიწეროს სხვა ფორმით. განსაზღვრების თანახმად:
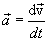 ,
,
მაშინ
 ანუ
ანუ 
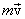 ვექტორს უწოდებენ სხეულის იმპულსს ან სხეულის მოძრაობის რაოდენობას და მიმართულებით იგი ემთხვევა
ვექტორს უწოდებენ სხეულის იმპულსს ან სხეულის მოძრაობის რაოდენობას და მიმართულებით იგი ემთხვევა  სიჩქარეს, ხოლო
სიჩქარეს, ხოლო 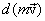 გამოსახავს ამ ვექტორის ცვლილებას.
გამოსახავს ამ ვექტორის ცვლილებას.
გარდავქმნათ უკანასკნელი გამოსახულება შემდეგნაირად:
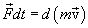 |
(3.6) |
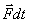 ვექტორს ეწოდება
ვექტორს ეწოდება 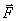 ძალის იმპულსი.
ძალის იმპულსი.
ეს განტოლება წარმოადგენს მატერიალური წერტილის დინამიკის ძირითადი კანონის გამოსახულებას: სხეულის იმპულსის ცვლილება მასზე მოქმედი ძალის იმპულსის ტოლია.


