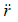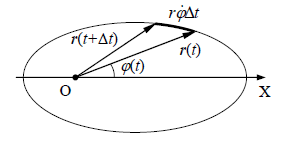
ამოცანის პირობის შესაბამისად შემოვიტანოთ პოლარული კოორდინატთა სისტემა პლანეტის მოძრაობის სიბრტყეში და მისი პოლუსი დავამთხვიოთ მზის მდებარეობას, ხოლო პოლარული ღერძი ემთხვევა ელიფსის ერთ-ერთ ღერძს. კეპლერის მეორე კანონის თანახმად პლანეტის σ სექტორული სიჩქარე, რომელიც ტოლია მატერიალური წერტილის (პლანეტის) რადიუს-ვექტორის მიერ შემოწერილი ფართობის ცვლილებისა, არის მუდმივი სიდიდე პლანეტის მზის ირგვლივ მოძრაობისას.
პოლარულ კოორდინატთა სისტემაში პლანეტის აჩქარების პროექციის მოსაძებნათ გამოვიენოთ ამოცანა 9-ში მიღებული ფორმულა (15):
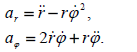
რადგან (1) განტოლებაში შედის პოლარული კოორდინატების დროითი წარმოებულები დავამატოთ ამ განტოლებას ტრაექტორიის განტოლება და გამოსახულება σ სექტორული სიჩქარისთვის:
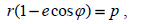
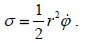
ამოცანის პირობის შესაბამისად σ სექტორული სიჩქარე მუდმივია პლანეტის ელიფსურ ტრაექტორიაზე მოძრაობისა, ამიტომ მისი დროითი წარმოებული ნულია:
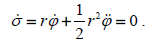
შევადაროთ (4) გამოსახულებას (1). ვხედავთ, რომ 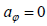

გავაწარმოოთ დროით (2) განტოლების ორივე მხარე.
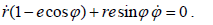
განტოლებების (2) და (3) გამოყენებით გარდავქმნათ განტოლება (5) შემდეგი სახით:
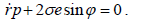
გავაწარმოოთ (6)-ის ორივე მხარე დროით
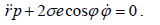
ისევ გამოვიყენოთ განტოლებები (2) და (3) რათა გამოვრიცხოთ 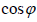
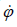
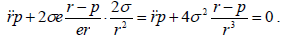
შედეგად მივიღებთ:
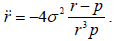
რათა ვიპოვნოთ აჩქარების პროექცია ar, როგორც მხოლოდ პოლარული კოორდინატების ფუნქცია ჩავსვათ
(8) გამოსახულებიდან და 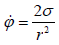
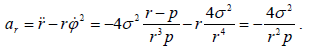
ამდენად, მზის ირგვლივ ელიფსურ ტრაექტორიაზე მოძრავი პლანეტის აჩქარება მიმართულია მზისკენ, არ არის დამოკიდებული პოლარულ კუთხეზე და უკუპროპორციულია მზემდე მანძილის კვადრატისა:

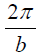
განვსაზღვროთ პოლარულ კოორდინატებში მატერიალური წერტილის სიჩქარისა და აჩქარების პროექციების დროზე დამოკიდებულება. ამისთვის გამოვიყენოთ ამოცანა 9-ში მიღებული (14) და (15) გამოსახულებები, მივიღებთ:
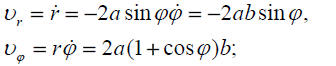
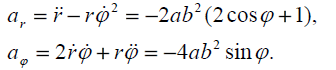
მაშინ სიჩქარისა და აჩქარების მოდულები იქნება:
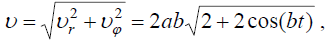
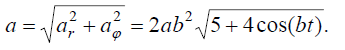
აღვნიშნოთ, რომ მატერიალური წერტილი 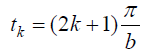
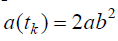
კლასიკურ ფიზიკაში, როგორც უკვე ვაჩვენეთ, მატერიალური წერტილის მდგომარეობა სრულად განისაზღვრება მისი კოორდინატებით х, у, z. და სიჩქარის კომპონენტებით 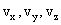 დროის მოცემულ მომენტში, ანუ
დროის მოცემულ მომენტში, ანუ 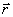 რადიუს ვექტორით და მისი სიჩქარით. მითითებული ფუნქციონალური დამოკიდებულებების გათვალისწინებით ნიუტონის მეორე კანონს აქვს სახე:
რადიუს ვექტორით და მისი სიჩქარით. მითითებული ფუნქციონალური დამოკიდებულებების გათვალისწინებით ნიუტონის მეორე კანონს აქვს სახე:
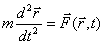 |
(3.14) |
თუ ჩავთვლით, რომ ცნობილია რეზულტატური ძალა 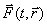 როგორც კოორდინატებისა და დროის ფუნქცია, მაშინ განტოლება (3.14) წარმოადგენს მეორე რიგის დიფერენციალურ განტოლებას მატერიალური წერტილის
როგორც კოორდინატებისა და დროის ფუნქცია, მაშინ განტოლება (3.14) წარმოადგენს მეორე რიგის დიფერენციალურ განტოლებას მატერიალური წერტილის 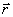 რადიუს-ვექტორის მიმართ.
რადიუს-ვექტორის მიმართ.
თუ ამოვხსნით (3.14) განტოლებას მოცემული მარჯვენა ნაწილით, შეიძლება განვსაზღვროთ სხეულის რადიუს-ვექტორი დროის ნებისმიერ მომენტში და ამით სხეულის მოძრაობის ტრაექტორია დავადგინოთ. ამასთან, მოძრაობის დამოუკიდებლობისგან გამომდინარე, რთულ ვექტორულ განტოლებას (3.14), რომელიც ზოგადად აღწერს სხეულის მრუდწირულ მოძრაობას, ცვლიან მისი ექვივალენტური სამი განტოლების სისტემით, თითოეული მათგანი აღწერს წრფივ მოძრაობას შესაბამისი х, у და z ღერძის გასწვრივ.
 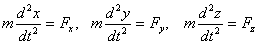 |
(3.15) |
სადაც 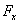 ,
, 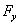 და
და 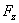 არის
არის 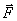 ვექტორის პროექციები კოორდინატთა ღერძებზე. х, у და z კოორდინატებს განსაზღვრავენ (3.15) განტოლების ორმაგი ინტეგრირებით. ყოველი ინტეგრირებისას წარმოიშვება განუსაზღვრელი მუდმივები. ამიტომ მოძრაობის კანონის ცალსახად გამოყოფისთვის აუცილებელია მოძრაობის განტოლებას დაემატოს ორი პირობა, რომელიც განსაზღვრავს ამ მუდმივებს. ამ პირობებს აფიქსირებენ, მატერიალური წერტილის მდგომარეობის მოცემით რაღაც მომენტში (ჩვეულებრივ საწყის მომენტში), ანუ მიუთითებენ რადიუს-ვექტორის
ვექტორის პროექციები კოორდინატთა ღერძებზე. х, у და z კოორდინატებს განსაზღვრავენ (3.15) განტოლების ორმაგი ინტეგრირებით. ყოველი ინტეგრირებისას წარმოიშვება განუსაზღვრელი მუდმივები. ამიტომ მოძრაობის კანონის ცალსახად გამოყოფისთვის აუცილებელია მოძრაობის განტოლებას დაემატოს ორი პირობა, რომელიც განსაზღვრავს ამ მუდმივებს. ამ პირობებს აფიქსირებენ, მატერიალური წერტილის მდგომარეობის მოცემით რაღაც მომენტში (ჩვეულებრივ საწყის მომენტში), ანუ მიუთითებენ რადიუს-ვექტორის 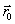 მნიშვნელობას ან კოორდინატების
მნიშვნელობას ან კოორდინატების 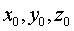 მნიშვნელობებს და სიჩქარის
მნიშვნელობებს და სიჩქარის 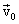 მნიშვნელობას საწყის t=0 მომენტში. ასეთნაირად, (3.15)-ის ინტეგრირების შედეგად ვღებულობთ х, у, z კოორდინატებს, როგორც დროისა და ინტეგრირების ორი მუდმივის ფუნქციებს:
მნიშვნელობას საწყის t=0 მომენტში. ასეთნაირად, (3.15)-ის ინტეგრირების შედეგად ვღებულობთ х, у, z კოორდინატებს, როგორც დროისა და ინტეგრირების ორი მუდმივის ფუნქციებს:
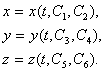
იმპულსის მუდმივობის კანონი არის ნიუტონის მეორე და მესამე კანონების შედეგი. მას ადგილი აქვს სხეულთა იზოლირებულ (ჩაკეტილ) სისტემაში.
იზოლირებული (ჩაკეტილი) ეწოდება სისტემას, რომლის თითოელ წევრზეც არ მოქმედებს გარეშე ძალები. იზოლირებულ სისტემაში თავს იჩენს შინაგანი ძალები, სისტემაში შემავალ სხეულბს შორის ურთიერთქმედების ძალები.
რადგან ჩაკეტილ სისტემაში გარეშე ძალები არ გვაქვს, ამიტომ
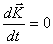
ანუ
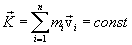 |
(3.13) |
ეს ტოლობა გამოხატავს იმპულსის მუდმივობის კანონს, რომლის თანახმადაც სხეულთა ჩაკეტილი სისტემის იმპულსის სრული ვექტორი დროთა განმავლობაში არ იცვლება.
რადგან 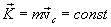 , ამიტომ ჩაკეტილ სისტემაში მიმდინარე ნებისმიერი პროცესის დროს, მისი ინერციის ცენტრის სიჩქარე უცვლელი რჩება.
, ამიტომ ჩაკეტილ სისტემაში მიმდინარე ნებისმიერი პროცესის დროს, მისი ინერციის ცენტრის სიჩქარე უცვლელი რჩება.