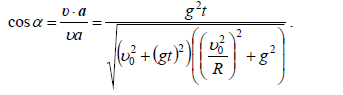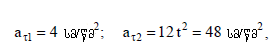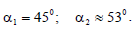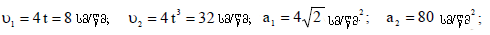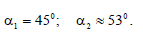განსაზღვრების თანახმად კუთხური აჩქარება არის კუთხური სიჩქარის პირველი წარმოებულია დროით:
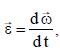
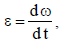
ამოცანის პირობის გათვალისწინებით, ვაწარმოოთ ცვლადთა განცალება და მივიღებთ:
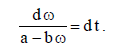
დროის საწყის მომენტში (როცა t =0) კუთხური სიჩქარე ტოლია 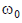
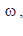
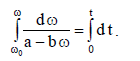
მივიღებთ: 
შესაბამისად 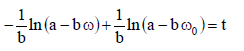
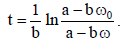
საიდანაც თანმიმდევრულად ვპოულობთ:
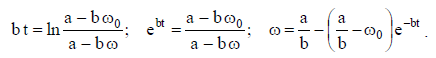
პასუხი: 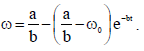
М1 და М2 წერტილების სიჩქარეები შეიძლება მოიძებნოს როგორც მათ მიერ განვლილი გზების წარმოებულები დროით:
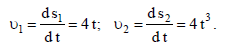
ამ წერტილების აჩქარებების ტანგენციალური მდგენელები მოიძებნება მათი წირითი სიჩქარეების დროითი წარმოებულებით:

ნორმალური მდგენელები იქნება (1)-ის გათვალისწინებით:

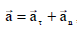
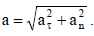
მაშინ (2)-ის და (3)-ის გათვალისწინებით ამ წერტილების სრული აჩქარების მოდულები იქნება:
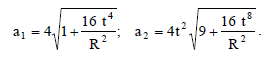
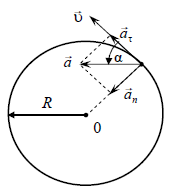
სრული აჩქარების მიმართულება განისაზღვრება სრულ აჩქარებასა და წირით სიჩქარეს (ანუ შესაბამისად ტანგენციურ აჩქარებას) შორის კუთხით ანუ . 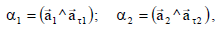
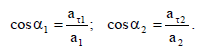
წერტილების პირველ შეხვედრამდე გასული დრო შეიძლება მოიძებნოს მანძილების გატოლებით S1=S2
8 + 2t2 = t4 ანუ t4 - 2t2 - 8 = 0 (7)
t > 0 შემთხვევაში ამ განტოლების ამოხსნა გვაძლევს:
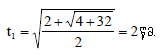
(1)-ში დროის მნიშვნელობის ჩასმით ვითვლით წერტილების სიჩქარეებს:

შემდეგ, ასევე (2)-ის მეშვეობით ვპოულობთ ტანგენტიურ აჩქარებებს:
(3)-ის მეშვეობით ვპოულობთ ნორმალურ აჩქარებებს:
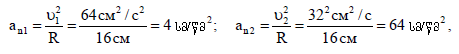
(5)-ის მეშვეობით ვპოულობთ სრულ აჩქარებებს:

განტოლებებით (6) ვიპოვნით სრული აჩქარებების მაჩვენებელ კუთხეებს
პასუხი:
ამოცანა 2.1
ორი წერტილი М1 და М2 მოძრაობენ ერთ წრეწირზე ერთი მიმართულებით შესაბამისად შემდეგი წესებით 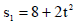
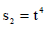
ამოცანა 2.2
ქანქარა ბორბლის ბრუნვისას მისი აჩქარება იცლებოდა 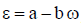
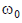
ამოცანა 2.3
R=0,5მ რადიუსის მქონე ბორბალი მოძრაობს გადატანითად v0=0,1მ/წმ სიჩქარით. ბორბლის რადიუსი ბრუნავს 2 ბრ / წმ სიხშირით. შეადგინეთ ბორბლის გარე გარსის А წერტილის მოძრაობის განტოლება და განსაზღვრეთ როგორ იცვლება დროში მისი სიჩქარის მოდული. განსაზღვრეთ, თუ როგორ მოძრაობს ბორბალი გზის მიმართ: მისრიალებს თუ ჭარბ ბრუნს აკეთებს.
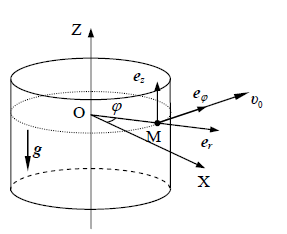
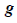
ჩავწეროთ საწყისი პირობები:

გამოვიყენოთ ამოცანა 9-ის (14) და (15) ფორმულები

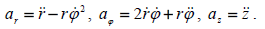
ამას გარდა ამოცანის პირობებიდან:

გამოვიყენოთ (2) – (4), მივიღებთ:
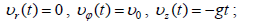
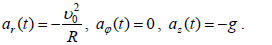
ამდენად, საძიებო სიჩქარესა და აჩქარებას ცილინდრულ კოორდინატებში აქვს სახე:
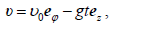
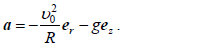
მოვძებნოთ სხეულის აჩქარებასა და სიჩქარეს შორის კუთხე α :