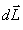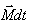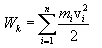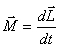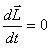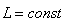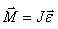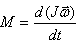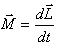ნებისმიერად მოძრავი სხეულის კინეტიკური ენერგია ტოლია ყველა იმ n მატერიალური წერტილის კინეტიკური ენერგიების ჯამისა, რომლებადაც შეიძლება ეს სხეული დაიყოს:
თუ სხეული ბრუნავს უძრავი ღერძის გარშემო 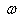
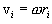
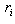
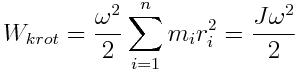 |
(5.11) |
სადაც J არის ღერძის მიმართ სხეულის ინერციის მომენტი.
ზოგადად მყარი სხეულის მოძრაობა შეიძლება წარმოვადგინოთ ორი მოძრაობის ჯამის სახით - გადატანითი სიჩქარით, რომელიც ტოლია მისი მასათა ცენტრის 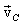
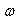
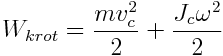 |
(5.12) |
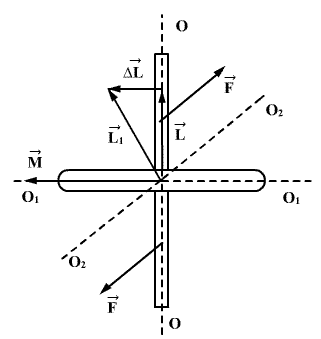
სადაც 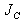
ჰიროსკოპის მოძრაობის რაოდენობის მომენტი ემთხვევა მისი ბრუნვის ღერძს. იმისთვის, რათა შევცვალოთ სივრცეში ჰიროსკოპის ღერძი, ანუ შევცვალოთ 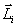

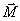
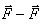
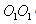
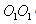
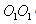

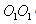
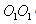
 ძალთა მომენტის მოქმედებით.
ძალთა მომენტის მოქმედებით. 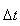
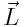 მიიღებს ნაზრდს
მიიღებს ნაზრდს 
 -ს. ჰიროსკოპის მოძრაობის რაოდენობის მომენტი
-ს. ჰიროსკოპის მოძრაობის რაოდენობის მომენტი  დროის შემდეგ იქნება
დროის შემდეგ იქნება  და ძევს ნახაზის სიბრტყეზე.
და ძევს ნახაზის სიბრტყეზე. 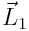 ვექტორის მიმართულება ემთხვევა ჰიროსკოპის ბრუნვის ღერძის ახალ მიმართულებას. ამდენად, ჰიროსკოპის ღერძი შემობრუნდება
ვექტორის მიმართულება ემთხვევა ჰიროსკოპის ბრუნვის ღერძის ახალ მიმართულებას. ამდენად, ჰიროსკოპის ღერძი შემობრუნდება 
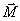
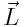 -ს შორის მცირდება: თუ ვიმოქმედებთ ჰიროსკოპზე ხანგრძლივად გარე ძალების მუდმივი მომენტით, მაშინ ჰიროსკოპის ღერძი საბოლოოდ დადგება ისე, რომ საკუთარი ბრუნვის ღერძი და მიმართულება დაემთხვევა გარე ძალების ზემოქმედებით ბრუნვის ღერძსა და მიმართულებას (ვექტორი
-ს შორის მცირდება: თუ ვიმოქმედებთ ჰიროსკოპზე ხანგრძლივად გარე ძალების მუდმივი მომენტით, მაშინ ჰიროსკოპის ღერძი საბოლოოდ დადგება ისე, რომ საკუთარი ბრუნვის ღერძი და მიმართულება დაემთხვევა გარე ძალების ზემოქმედებით ბრუნვის ღერძსა და მიმართულებას (ვექტორი 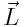 , ემთხვევა მიმართულებით
, ემთხვევა მიმართულებით 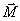
ბრუნვითი მოძრაობის დინამიკის ძირითადი განტოლებიდან გამომდინარეობს, რომ
ჩაკეტილი (იზოლირებული) სისტემისთვის სხეულზე მოქმედი ყველა გარე ძალის მომენტის ვექტორი 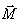
ანუ
ეს არის მოძრაობის რაოდენობის მომენტის მუდმივობის კანონი და ასე ფორმულირდება: თუ სისტემაზე მოქმედი ყველა ძალის ჯამური მომენტი სისტემის უძრავი ბრუნვის ღერძის მიმართ ნულის ტოლია, მაშინ ამ ღერძის მიმართ იმპულსის მომენტი არ იცვლება მოძრაობის პროცესში.
(5.8) განტოლების თანახმად ნიუტონის მეორე კანონი ბრუნვითი მოძრაობისთვის არის
განსაზღვრების თანახმად კუთხური აჩქარება არის 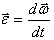
(5.9) განტოლების გათვალისწინებით
ანუ
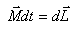 |
(5.10) |
ამ გამოსახულებას ეწოდება ბრუნვითი მოძრაობის დინამიკის ძირითადი განტოლება და ასე ფორმულირდება: მყარი სხეულის მოძრაობის რაოდენობის ცვლილება