თუ დრეკადი (მყარი, თხევადი ან აირადი) გარემოს რაიმე ადგილას აღვძრავთ მისი ნაწილაკების რხევებს, მაშინ ნაწილაკებს შორის ურთიერთქმედების შედეგად ეს რხევები დაიწყებს გავრცელებას გარემოში რაღაც v სიჩქარით. რხევების გავრცელების პროცესს ეწოდება ტალღა. ტალღას გარემოში გავრცელებისას ნაწილაკები არ გადააქვს. ნაწილაკები მხოლოდ ირხევიან საკუთარი წონასწორული მდგომარეობის მიდამოში. ნაწილაკების რხევის მიმართულების ტალღის გავრცელების მიმართულებასთან დამოკიდებულებით ასხვავებენ გასწვრივ და განივ ტალღებს. გასწვრივ ტალღაში ნაწილაკები ირხევა ტალღის გავრცელების მიმართულების გასწვრივ. განივ ტალღაში გარემოს ნაწილაკები ირხევა ტალღის გავრცელების მიმართულები მართობულად. მექანიკური განივი ტალღები შეიძლება აღიძრას მხოლოდ ისეთ გარემოში, რომელსაც აქვს წანაცვლების წინაღობა. ამიტომ თხევად და აირად გარემოებში აღიძრება მხოლოდ გასწვრივი ტალღები. მყარ სხეულებში შეიძლება ორივე ტიპის ტალრების აღძვრა. გასწვრივ ტალრებში, ნაწილაკების წანაცვლებისა და ტალღის მიმართულების თანხვედრის გამო წარმოიშვება შემჭიდროებები და გაუხშოებები.
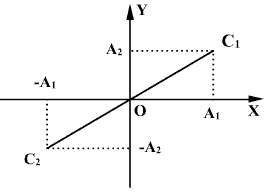
ტალრების გავრცელება დრეკად გარემოში
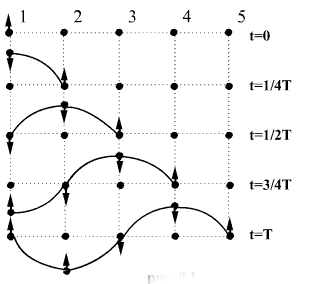
ნახაზზე ნაჩვენებია ნაწილაკების მოძრაობა გარემოში განივი ტალღის გავრცელების დროს. ნომრებით 1,2,3 და ა.შ. აღნიშნულია ერთმანეთისგან νT/4 (რხევის მეოთხედ პერიოდში ტალღის მიერ განვლილი მანძილი) მანძილებით დაშორებული ნაწილაკები. საწყიის მომენტში (t = 0) ყველა წერტილი განლაგებულია წრფეზე და არცერთი არ არის გამოსული წონასწორობის მდგომარეობიდან. მოვიყვანოთ წერტილი 1 ჰარმონიულ რხევაში Т პერიოდით, 1-5 წრფის პერპენდიკულარული მიმართულებით. რადგან გარემოს ნაწილაკები დრეკადობით არიან ურთიერთკავშირში, ისინიც იწყებენ რხევას, მაგრამ რაღაც დაგვიანებით. რხევის ნახევარი პერიოდის (t=T/4) შემდეგ წერტილი 1 გადაიხრება წრფიდან მაქსიმალური წანაცვლებით. t=T/4 დროის ამოწურვის შემდეგ წერტილი 2-იც დაიწყებს აწევას. როცა t=T/2 , პირველი წერტილი დაუბრუნდება წონასწორობის მდგომარეობას, რომელსაც წერტილი აღწევს, მეორე წერტილი აღწევს მაქსიმალურ გადახრას და რხევა აღწევს წერტილ 3-თან. როცა t=3T/4 წერტილი 1 აღწევს მაქსიმალურ უარყოფით წანაცვლებას, წერტილი 2 უბრუნდება წონასწორობის მდგომარეობას და რხევა მიაღწევს წერტილ 4-ს. ბოლოს t = Т დროის შემდეგ წერტილი 1 უბრუნდება წონასწორობის მდგომარეობას, შეასრულებს რა ერთ სრულ რხევას. რხევებმა მიაღწიეს წერტილ 5-მდე და ყველა მერხევი წერტილი ქმნის ტალღას. შემდგომი რხევების განმავლობაში პროცესი გავრცელდება წერტილი 5-ის მარჯვნივ. განხილულ შემთხვევაში ყოველი ნაწილაკი მოძრაობს მხოლოდ ქვემოტკენ და ზემოთკენ. დამკვირვებელს კი ექმნება შტაბეჭდილება, რომ "ტალღა გარბის", თუმცა ხდება მხოლოდ ერთი წერტილიდან მეორე წერტილში მოძრაობის გადაცემა.
(t = Т) პერიოდის ტოლი დროის მომენტში წონასწორობის მდგომარეობაში მყოფ წერტილებს 1 და 5 აქვთ ერთნაირი წანაცვლება და წანაცვლების ერთნაირი მიმართულება. ამიტომ ამბობენ, რომ 1 და 5 წერტილებს აქვთ ერთნაირი ფაზები. მათგან განსხვავებით წერტილები 1 და 3, თუმცა მათ აქვთ ტოლი წანაცვლება, მოძრაობენ ურთიერთსაპირისპირო მიმართუელბებით. ამიტომ ამბობენ, რომ წერტილები 1 და 3 იმროფებიან ურთიერთსაპიროსპირო ფაზებში. 1 და 5 წერტილებს შორის მანძილი განსაზღვრავს ტალღის სიგრძეს, ანუ ტალღის სიგრძე λ ეწოდება ტალღის ერთ ფაზაში მერხევ ორ უახლოეს წერტილებს შორის მანძილს. ტალღის პერიოდი Т ეწოდება მისი წერტილების ერთი სრული რხევის დროს. პერიოდის შებრუნებულ სიდიდეს უწოდებენ ტალღის სიხშირეს. ტალღის სიჩქარე განისაზღვრება გარემოს ერთი წერტილიდან მეორე წერტილამდე რხევის გადაცემის სიჩქარით: v=λ/T რადგან T=1/ν ამიტომ,
| v=λν | (8.1) |
ტალრების გავრცელების სიჩქარე მით ნაკლებია, რაც უფრო ინერტულია გარემო, ანუ რაც მეტია მისი სიმკვრივე. მეორეს მხრივ სიჩქარეს აქვს მეტი მნიშვნელობა მეტად დრეკად გარემოში. გასწვრივი ტალღების სიჩქარე განისაზღვრება ფორმულით: \(v_{\parallel}=\sqrt{\frac{E}{\rho }}\), განივისა კი: \(v_{\perp }=\sqrt{\frac{G}{\rho }}\), სადაც ρ- გარემოს სიმკვრივეა, E - იუნგის მოდულია, G - წანაცვლების მოდულია. რადგან მყარი სხეულების უმეტესობისთვის E>G , ამიტომ გასწვრივი ტალრების სიჩქარე მეტია განივი ტალღების სიჩქარეზე.
იძულებითი რხევების შემთხვევაში მერხევი სისტემა ირხევა გარე (მაიძულებელი) ძალის ზემოქმედებით, და ამ ძალის მიერ შესრულებული მუშაობის ხარჯზე პერიოდულად კომპენსირდება სისტემის ენერგიის დანაკარგი. იძულებითი რხევების სიხშირე (მაიძულებელი სიხშირე) დამოკიდებულია გარე ძალის ცვლილების სიხშირეზე. განვსაზღვროთ m მასის სხეულის იძულებითი რხევის ამპლიტუდა. რხევა ჩავთვალოთ მიულევლად Fext ძალის მუდმივი მოქმედების გამო.
ვთქვათ ეს ძალა დროის მიხედვით შემდეგნაირად იცვლება Fext=F0cosωt , სადაც F0 არის მაიძულებელი ძალის ამპლიტუდა Fext. დამაბრუნებელი ძალა Fext=-kx და წინაღობის ძალა Fext=rv მაშინ ნიუტონის მეორე კანონს ჩავწერთ ასე:
ma=-kx-rv+F0cosωt
ანუ
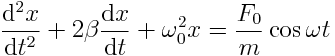 |
(7.21) |
დავუშვათ, რომ ძალის ზემოქმედებით სისტემის დამდგარი იძულებითი რხევები ასევე არის ჰარმონიული:
x=-Asin(ωt+φ0) (7.22)
ამასთან მათი ციკლური სიხშირე ტოლია მაიძულებელი ძალის ω სიხშირისა.
გავაწარმოოთ (7.22) ორჯერ და ჩავსვათ (7.21)-ში, მივიღებთ
ω2cos(ωt+φ0+π/2)+2βω2cos(ωt+φ0)+ω02cos(ωt+φ0-π/2)=(F0/mA)cos(ωt)
აღვნიშნოთ: A1=ω2, A2=2βω2, A3=ω02, A4=(F0/mA)
მაშინ ბოლო ტოლობა შეიძლება ასე ჩავწეროთ:
A1cos(ωt+φ0+π/2)+A2cos(ωt+φ0)+A3cos(ωt+φ0-π/2)=A4cos(ωt)
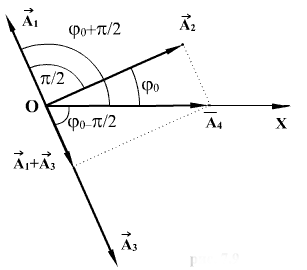
ამ გამოსახულების მარჯვენა მხარე შეიძლება განვიხილოთ როგორც რაღაც ჰარმონიული რხევის განტოლება, რომელიც მიიღება იმ სამი ჰარმონიული რხევის შეკრებით, რომლებიც ამ ტოლობის მარცხენა მხარით განისაზღვრება. ამ რხევების შესაკრებად გამოვიყენოთ ვექტორული დიაგრამების მეთოდი. გავავლოთ ОХ საყრდენი ხაზი და მოვჭიმოთ საწყისი ფაზების შესაბამისი ოთხივე კუთხე და გადავზომოთ მათი შესაბამისი ამპლიტუდების ვექტორები 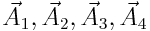 ისე, რომ
ისე, რომ
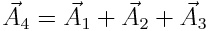
ნახაზიდან ჩანს, რომ 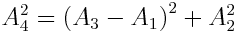 ჩავსვათ აქ ამპლიტუდების შესაბამისი მნიშვნელობები (1.22)-ის მიხედვით, მივიღებთ:
ჩავსვათ აქ ამპლიტუდების შესაბამისი მნიშვნელობები (1.22)-ის მიხედვით, მივიღებთ:
\(\dpi{120} \frac{F_{0}^{2}}{m^{2}A^{2}}=\left ( \omega _{0}^{2}-\omega ^{2} \right )^{2}+4\omega ^{2}\beta ^{2}\)
აქედან
| \(\dpi{120} A=\frac{F_{0}}{m\sqrt{\left ( \omega _{0}^{2}-\omega ^{2} \right )^{2}+4\omega ^{2}\beta ^{2}}}\) | (7.23) |
დამდგარი იძულებითი რხევების ამპლიტუდა პირდაპირპროპორციულია მაიძულებელი ძალის F0 ამპლიტუდისა, უკუპროპორციულია სისტემის m მასისა და მცირდება მილევის β კოეფიციენტის ზრდით. როცა F0, m და β მუდმივებია, ამპლიტუდა დამოკიდებულია მხოლოდ მაიძულებელი ძალის ციკლური ω სიხშირისა და სისტემის თავისუფალი არამილევადი რხევების ω0 სიხშირის თანაფარდობაზე. როცა მაიძულებელი ძალის ციკლური სიხშირე ω=0, მაშინ რცხევების ამპლიტუდა 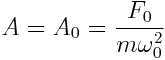 . ამ შემთხვევაში რხევები არ ხდება და წანაცვლება არის სტატიკური დეფორმაცია მუდმივი F0 ძალის გავლენით:
. ამ შემთხვევაში რხევები არ ხდება და წანაცვლება არის სტატიკური დეფორმაცია მუდმივი F0 ძალის გავლენით:
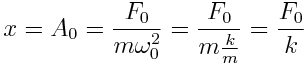
ამიტომ A0 გადახრას ხანდახან სტატიკურ ამპლიტუდას უწოდებენ.
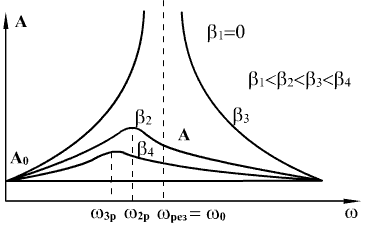
თუ არ არის დისიპაცია ანუ β=0, მაში რხევების ამპლიტუდა
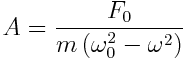
იზრდება მაიძულებელი Fdr ძალის ω ციკლური სიხშირის ზრდით და როცა ω=ω0 ხდება უსასრულოდ დიდი. ω ციკლური სიხშირის შემდგომი ზრდით იძულებითი რხევების А ამპლიტუდა მცირდება, ამასთან 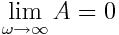 .
.
მაიძულებელი ω სიხშირის სისტემის ω0 საკუთარ სიხშირესთან მიახლოებისას იძულებითი რხევების ამპლიტუდის მკვეთრი ზრდის მოვლენას რეზონანსი ეწოდება.
თუ გვაქვს მილევა (β≠0), მაშინ იძულებითი რხევების ამპლიტუდა აღწევს მაქსიმალურ მნიშვნელობას, როცა (7.23) განტოლებაში მარჯვენა მხარის მნიშვნელი აღწევს მინიმუმს. გავუტოლოთ ნულს ფესქვეშა გამოსახულების ω-თი პირველი წარმოებული, მივიღებთ მისი მინიმუმის პირობას 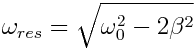 , სადაც ωres-ს უწოდებენ რეზონანსულ სიხშირეს. ωres აღნიშნავს ω ციკლური სიხშირის იმ მნიშვნელობას, რომლისთვისაც A=Amax.
, სადაც ωres-ს უწოდებენ რეზონანსულ სიხშირეს. ωres აღნიშნავს ω ციკლური სიხშირის იმ მნიშვნელობას, რომლისთვისაც A=Amax.
უკანასკნელი ფორმულიდან გამომდინარეობს, რომ კონსერვატული სისტემისთვის (β=0) ωres=ω0, ხოლო დისიპაციური სისტემისთვის ωres რამდენადმე ნაკლებია საკუთარ ციკლურ სიჩქარეზე. მილევის კოეფიციენტის გაზრდით რეზონანსის მოვლენა სულ ურო სუსტად ვლინდება და ბოლოს, როცა 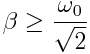 რეზონანსი სულაც ქრება.
რეზონანსი სულაც ქრება.
რეზონანსის მოვლენა გამოიყენება რხევების, მაგალითად ელექტრომაგნიტური რხევების გასაძლიერებლად. მეორეს მხრივ სხვადასხვა მანქანებისა და ნაგებობების კონსტრუირებისას უნდა გათვალისწინებული იქნას თუნდაც სულ მცირე პერიოდული ძალებიც კი, რათა თავიდან აცილებულ იქნას რეზონანსის არასასურველი შედეგები.
ყვეკლა რეალური მერხევი სისტემა არის დისიპაციური. ასეთი მექანიკური რხევების ენერგია თანდათან იხარჯება ხახუნის ძალის წინააღმდეგ მუშაობის შესრულებაზე, ამიტომ თავისუფალი რხევები ყოველთვის მიილევა - მათი ამპლიტუდა თანდათან მცირდება. ბევრ შემთხვევაში, როცა არ არის მშრალი ხახუნი, პირველ მიახლოებაში შეიძლება ჩაითვალოს, რომ მოძრაობის მცირე სიჩქარეების შემთხვევაში, მექანიკური რხევის მილევის გამომწვევი ძალები პროპორციულია სიჩქარის. ამ ძალებს, მათი წარმოშობის მიუხედავად, უწოდებენ წინაღობის (მიმლევ ძალებს Fd) ძალებს.
| Fd=-rv, | (7.17) |
სადაც r - წინაღობის კოეფიციენტია, v - მოძრაობის სიჩქარე. ОХ ღერძის გასწვრივ ჩავწეროთ მილევადი რხევისთვის ნიუტონის მეორე კანონი ma=-kx-rv,
ანუ
 |
(7.18) |
გადავწეროთ ეს განტოლება ასე: 
და აღვნიშნოთ:\(\dpi{120} \frac{r}{m}=2\beta\) ; 
სადაც  წარმოადგენს იმ სიხშირეს, რომლითაც შესრულდებოდა სისტემის თავისუალი რხევები გარემოს წინაღობის არარსებობის შემთხვევაში, ანუ როცა r = 0. ამ სიხშირეს უწოდებენ სისტემის საკუთარ სიხშირეს; β - არის მილევის კოეფიციენტი. მაშინ
წარმოადგენს იმ სიხშირეს, რომლითაც შესრულდებოდა სისტემის თავისუალი რხევები გარემოს წინაღობის არარსებობის შემთხვევაში, ანუ როცა r = 0. ამ სიხშირეს უწოდებენ სისტემის საკუთარ სიხშირეს; β - არის მილევის კოეფიციენტი. მაშინ
 |
(7.19) |
ვეძებთ (7.19) განტოლების ამოხსნას შემდეგი სახით

სადაც U - t-ს რაღაც ფუნქციაა.
გავაწარმოოთ ორჯერ t დროით, ჩავსვათ პირველი და მეორე წარმოებულები (7.19)-ში და მივიღებთ \(\dpi{120} \frac{\mathrm{d} ^{2}U}{\mathrm{d} t^{2}}+\left ( \omega _{0}^{2}-\beta ^{2} \right )U=0\)
ამ განტოლების ამოხსნა მნიშვნელოვნად არის დამოკიდებული U-სთან მდგომი კოეფიციენტის ნიშანზე. განვიხილოთ შემთხვევა, როცა ეს კოეფიციენტი დადებითია. შემოვიტანოთ აღნიშვნა  , მაშინ ამ განტოლების ამოხსნა ნამდვილი ω-თი იქნება, როგორც ვიცით, ფუნქცია
, მაშინ ამ განტოლების ამოხსნა ნამდვილი ω-თი იქნება, როგორც ვიცით, ფუნქცია 
ამდენად, გარემოს მცირე წინაღობის ( ) შემთხვევაში, (7.19) განტოლების ამოხსნა იქნება შემდეგი ფუნქცია
) შემთხვევაში, (7.19) განტოლების ამოხსნა იქნება შემდეგი ფუნქცია
 |
(7.20) |
ამ ფუნქციის გრაფიკი გამოსახულია ნახაზზე. წყვეტილი წირებით გამოსახულია საზღვრები, რომელშიც იმყოფება მერხევი წერტილის წანაცვლებები.  სიდიდეს უწოდებენ დისიპაციური სისტემის რხევის საკუთარ ციკლურ სიხშირეს. მილევადი რხევები წარმოადგენს არაპერიოდულ რხევებს, რადგან მათში არასდროს არ მეორდება, მაგალითად, წანაცვლების, სიჩქარისა და აჩქარების მაქსიმალური მნიშვნელობები. სიდიდეს \(\dpi{120} T=\frac{2\pi }{\omega }\) ჩვეულებრივ უწოდებენ მილევადი რხევების პერიოდს, ურო სწორედ - მილევადი რხევების პირობით პერიოდს.
სიდიდეს უწოდებენ დისიპაციური სისტემის რხევის საკუთარ ციკლურ სიხშირეს. მილევადი რხევები წარმოადგენს არაპერიოდულ რხევებს, რადგან მათში არასდროს არ მეორდება, მაგალითად, წანაცვლების, სიჩქარისა და აჩქარების მაქსიმალური მნიშვნელობები. სიდიდეს \(\dpi{120} T=\frac{2\pi }{\omega }\) ჩვეულებრივ უწოდებენ მილევადი რხევების პერიოდს, ურო სწორედ - მილევადი რხევების პირობით პერიოდს.
დროში Т პერიოდით ერთმანეთის თანმიმდევრობით მიმდინარე წანაცვლებათა ამპლიტუდების ფარდობის ნატურალურ ლოგარითმს უწოდებენ მილევის ლოგარითმულ დეკრემენტს.
\(\dpi{120} \delta =ln\frac{e^{-\beta T}\sin \left ( \omega t+\varphi _{0} \right )}{e^{-\beta \left (1+T \right )}\sin \left ( \omega t+\varphi _{0} \right )}=lne^{\beta T}=\beta T\)
აღვნიშნოთ τ-თი დროის მონაკვეთი, რომელშიც რხევების ამპლიტუდა მცირდება е-ჯერ. მაშინ

საიდანაც

შესაბამისად, მილევის კოეფიციენტი არის ფიზიკური სიდიდე, რომელიც არის იმ τ დროის შებრუნებული, რომლის განმავლობაშიც ამპლიტუდა მცირდება е ჯერ. τ სიდიდეს უწოდებენ რელაქსაციის დროს.
ვთქვათ N - არის რხევათა რიცხვი, რომლის შემდეგაც ამპლიტუდა მცირდება е-ჯერ. მაშინ

შესაბამისად, რხევის ლოგარითმული დეკრემენტი δ არის ფიზიკური სიდიდე, რომელიც არის იმ N რხევათა რიცხვის შებრუნებული, რომლის შესრულების შემდეგ ამპლიტუდა კლებულობს е-ჯერ
საერთო წრფის გასწვრივ მიმართული ჰარმონიული რხევების შეკრება.
განვიხილოთ ერთპერიოდიანი ერთნაირი მიმართულების რხევები, რომელთაც აქვთ განსხვავებული საწყისი ფაზები და ამპლიტუდები. შესაკრები რხევების განტოლებები მოცემულია შემდი სახით:
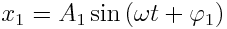 ,
,
 ,
,
სადაც x1 და x2 - წანაცვლებებია; A1 და A2 - ამპლიტუდები; ϕ1 და ϕ2 - შესაკრები რხევების საწყისი ფაზები. ჯამური რხევის ამპლიტუდის განსაზღვრა მოსახერხებელია ვექტორული დიაგრამით, რომელზეც გადაზომილია 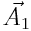 და
და 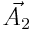 ამპლიტუდების ვექტორები х-ისადმი ϕ1 და ϕ2 კუთხეებით და პარალელოგრამის წესით მიღებულია ჯამური რხევის ამპლიტუდა
ამპლიტუდების ვექტორები х-ისადმი ϕ1 და ϕ2 კუთხეებით და პარალელოგრამის წესით მიღებულია ჯამური რხევის ამპლიტუდა 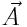 . თუ თანაბრად ვაბრუნებთ ვექტორთა სისტემას (პარალელოგრამს) და ვექტორებს დავაგეგმილებთ OY ღერძზე, მაშინ მათი მდგენელები შეასრულებენ ჰარმონიულ რხევებს მოცემული განტოლებების შესაბამისად.
. თუ თანაბრად ვაბრუნებთ ვექტორთა სისტემას (პარალელოგრამს) და ვექტორებს დავაგეგმილებთ OY ღერძზე, მაშინ მათი მდგენელები შეასრულებენ ჰარმონიულ რხევებს მოცემული განტოლებების შესაბამისად. 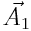 და
და 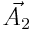 ვექტორების ურთიერთგანლაგება, ამასთან, არ იცვლება, ამიტომ ჯამური
ვექტორების ურთიერთგანლაგება, ამასთან, არ იცვლება, ამიტომ ჯამური 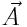 ვექტორის პროექციის რხევაც იქნება ჰარმონიული.
ვექტორის პროექციის რხევაც იქნება ჰარმონიული.

აქედან ვასკვნით, რომ ჯამური მოძრაობა არის ჰარმონიული რხევა, რომელსაც აქვს განსაზღვრული ციკლური სიხშირე. განვსაზღვროთ ჯამური რხევის. სამკუთხედში ΔOK1K კუთხე OK1K=[π-(ϕ2-ϕ1)] (პარალელოგრამის მოპირისპირე კუთხეების ტოლობიდან გამომდინარე).
შესაბამისად
2(ϕ2-ϕ1)+2α=2π
აქედან
α=[π-(ϕ2-ϕ1)]
კოსინუსების თეორემის თანახმად
A2=A12+A22-2A1A2cos[π-(ϕ2-ϕ1)]
ანუ
| A2=A12+A22-2A1A2cos(ϕ2-ϕ1) | (7.12) |
ჯამური რხევის საწყისი ფაზა ϕ0 განისაზღვრება ΔOKD-დან :
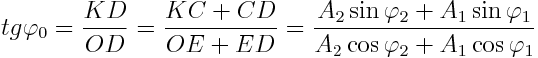
თანაფარდობები ფაზისა და ამპლიტუდისთვის საშუალებას გვაძლევს მოვძებნოთ ჯამური მოძრაობის ამპლიტუდა და საწყისი ფაზა და შევადგინოთ მისი განტოლება
x=Asin(ωt+ϕ)
ფეთქვა
განვიხილოთ შემთხვევა, როცა ორი შესაკრები რხევის სიხშირეები განსხვავდებიან ერთმანეთისგან სიდიდით ω2-ω1=Δω, და ვთქვათ მათი ამპლიტუდები ერთნაირია ხოლო საწყისი ფაზები ϕ0=0 , ანუ x1=Asin(ω1t), x2=Asin(ω2t). შევკრიბოთ ეს განტოლებები ანალიზურად
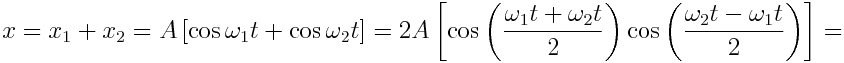

გარდავქმნათ
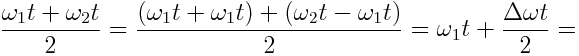

მაშინ
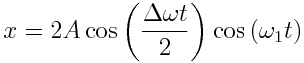
რადგან 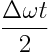 მაინც ნელა იცვლება, სიდიდეს
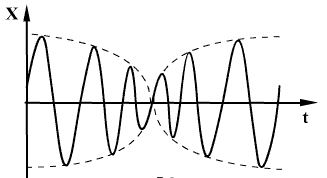
მაინც ნელა იცვლება, სიდიდეს 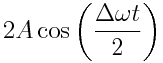 ვერ ვუწოდებთ ამპლიტუდას ამ სიტყვის სრული გაგებით (ამპლიტუდა მუდმივი სიდიდეა). პირობითად ამ სიდიდეს შეიძლება ვუწოდოთ ცვლადი ამპლიტუდა. ასეთი რხევების გრაიკი მოცემულია ნახაზზე. შესაკრებ რხევებს აქვთ ერთნაირი ამპლიტუდები, მაგრამ განსხვავებული პერიოდები, ამასთან T1 da T2 მცირედ განსხვავდება ერთმანეთისგან. ასეთი რხევების შეკრებისას დაიმზირება ფეთქვა. წამში ფეთქვათ n რიცხვი განისაზღვრება შესაკრები რხევების სიხშირეთა სხვაობით, ანუ
ვერ ვუწოდებთ ამპლიტუდას ამ სიტყვის სრული გაგებით (ამპლიტუდა მუდმივი სიდიდეა). პირობითად ამ სიდიდეს შეიძლება ვუწოდოთ ცვლადი ამპლიტუდა. ასეთი რხევების გრაიკი მოცემულია ნახაზზე. შესაკრებ რხევებს აქვთ ერთნაირი ამპლიტუდები, მაგრამ განსხვავებული პერიოდები, ამასთან T1 da T2 მცირედ განსხვავდება ერთმანეთისგან. ასეთი რხევების შეკრებისას დაიმზირება ფეთქვა. წამში ფეთქვათ n რიცხვი განისაზღვრება შესაკრები რხევების სიხშირეთა სხვაობით, ანუ
n=ν1-ν2
ფეთქვას შეიძლება დავაკვირდეთ ორი კამერტონის ჟღერისას, როცა მათი სიხშირეები ახლოს არის ერთმანეთთან.
ურთიერთმართობი რხევების შეკრება.
ვთქვათ მატერიალური წერტილი ერთდროულად მონაწილეობას ორ ჰარმონიულ რხევაში, რომლებიც ერთნაირი Т პერიოდით მიმდინარეობს ორ ურთიერთმართობი მიმართულებით. ამ მიმართულებებს მივაბათ მართკუთხა XOY კოორდინატთა სისტემა, ისე, რომ კოორდინატთა სათავე მოვათავსოთ მატერიალური წერტილის წონასწორობის მდგომარეობის მდებარეობაში. ОХ და OY ღერძების მიმართ წერტილის წანაცვლებები აღვნიშნოთ, შესაბამისად, х-ით და у-ით.
განვიხილოთ რამდენიმე კერძო შემთხვევა.
ა. რხევების საწყისი ფაზები ტოლია. ავირჩიოთ დროის ათვლის საწყისი ისე, რომ საწყისი ორივე რხევის საწისი ფაზები იყოს ნული. მაშინ წანაცვლებები ОХ და OY ღერძების გასწვრივ გამოისახება შემდეგი განტოლებებით:
x=A1sin(ωt), y=A2sin(ωt)
შევაფარდოთ ამ განტოლებების მხარეები და მივიღებთ С წერტილის ტრაექტორიის განტოლებას:
 ანუ
ანუ 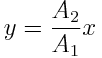
შესაბამისად, ორი ურთიერთმართობი რხევის შეკრების შედეგად წერტილი С ირხევა С1С2 წრფის გასწვრივ, რომელიც კოორდინატთა სათავეზე გადის.
ბ. ფაზათა საწყისი სხვაობა ტოლია π ამ შემთხვევაში რხევისს განტოლებას აქვს სახე:
x=A1sin(ωt+π)=-A1sin(ωt), y=A2sin(ωt)
წერტლის ტრაექტორიის განტოლებაა
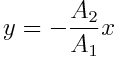 |
(7.15) |
შესაბამისად, წერტილი С ირხევა С1С2 მონაკვეთის გასწვრივ, იმ წრფისა, რომელიც გადის კოორდინატთა სათავეზე, მაგრამ იმყოფება პირველი შემთხვევისგან განსხვავებულ კვანდრანტებში. ჯამური რხევის А ამპლიტუდა ორივე განხილულ შემთხვევაში ტოლია
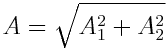
გ. ფაზათა საწყისი სხვაობა ტოლია  .
.
რხევის განტოლებას აქვს სახე:
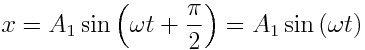 ,
, 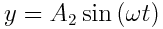
გავყოთ პირველი განტოლება A1-ზე , მეორე - A2-ზე :
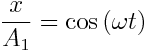 ,
, 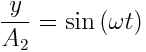
ორივე ტოლობა ავიყვანოთ კვადრატში და შევკრიბოთ. მივიღებთ მერხევი წერტილის მოძრაობის ტრაექტორიის შემდეგ განტოლებას
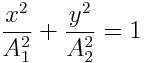 |
(7.16) |
С მერხევი წერტილი მოძრაობს ელიფსზე, რომლის ნახევარღერძებია A1 და A2. ტოლი ამპლიტუდების დროს A1=A2=A ჯამური მოძრაობის ტრაექტორია იქნება წრეწირი x2+y2=A2. ზოგად შემთხვევაში, როცა ω1≠ω2, მაგრამ ჯერადია, ანუ ω1=kω2, ურთიერთპერპენდიკულარული რხევების შეკრებისა წერტილი მოძრაობს მრუდებზე, რომლებსაც ლისაჟუს მრუდები ეწოდება. ამ მრუდების კონფიგურაცია დამოკიდებულია შემადგენელი რხევების ამპლიტუდების, საწყისი ფაზებისა და პერიოდების თანაფარდობებზე.