იძულებითი რხევების შემთხვევაში მერხევი სისტემა ირხევა გარე (მაიძულებელი) ძალის ზემოქმედებით, და ამ ძალის მიერ შესრულებული მუშაობის ხარჯზე პერიოდულად კომპენსირდება სისტემის ენერგიის დანაკარგი. იძულებითი რხევების სიხშირე (მაიძულებელი სიხშირე) დამოკიდებულია გარე ძალის ცვლილების სიხშირეზე. განვსაზღვროთ m მასის სხეულის იძულებითი რხევის ამპლიტუდა. რხევა ჩავთვალოთ მიულევლად Fext ძალის მუდმივი მოქმედების გამო.
ვთქვათ ეს ძალა დროის მიხედვით შემდეგნაირად იცვლება Fext=F0cosωt , სადაც F0 არის მაიძულებელი ძალის ამპლიტუდა Fext. დამაბრუნებელი ძალა Fext=-kx და წინაღობის ძალა Fext=rv მაშინ ნიუტონის მეორე კანონს ჩავწერთ ასე:
ma=-kx-rv+F0cosωt
ანუ
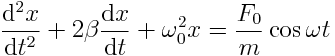 |
(7.21) |
დავუშვათ, რომ ძალის ზემოქმედებით სისტემის დამდგარი იძულებითი რხევები ასევე არის ჰარმონიული:
x=-Asin(ωt+φ0) (7.22)
ამასთან მათი ციკლური სიხშირე ტოლია მაიძულებელი ძალის ω სიხშირისა.
გავაწარმოოთ (7.22) ორჯერ და ჩავსვათ (7.21)-ში, მივიღებთ
ω2cos(ωt+φ0+π/2)+2βω2cos(ωt+φ0)+ω02cos(ωt+φ0-π/2)=(F0/mA)cos(ωt)
აღვნიშნოთ: A1=ω2, A2=2βω2, A3=ω02, A4=(F0/mA)
მაშინ ბოლო ტოლობა შეიძლება ასე ჩავწეროთ:
A1cos(ωt+φ0+π/2)+A2cos(ωt+φ0)+A3cos(ωt+φ0-π/2)=A4cos(ωt)
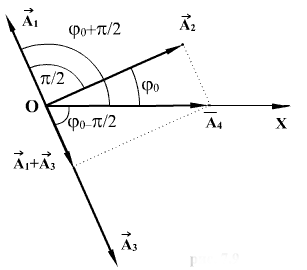
ამ გამოსახულების მარჯვენა მხარე შეიძლება განვიხილოთ როგორც რაღაც ჰარმონიული რხევის განტოლება, რომელიც მიიღება იმ სამი ჰარმონიული რხევის შეკრებით, რომლებიც ამ ტოლობის მარცხენა მხარით განისაზღვრება. ამ რხევების შესაკრებად გამოვიყენოთ ვექტორული დიაგრამების მეთოდი. გავავლოთ ОХ საყრდენი ხაზი და მოვჭიმოთ საწყისი ფაზების შესაბამისი ოთხივე კუთხე და გადავზომოთ მათი შესაბამისი ამპლიტუდების ვექტორები 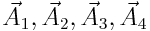 ისე, რომ
ისე, რომ
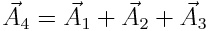
ნახაზიდან ჩანს, რომ 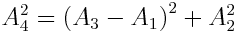 ჩავსვათ აქ ამპლიტუდების შესაბამისი მნიშვნელობები (1.22)-ის მიხედვით, მივიღებთ:
ჩავსვათ აქ ამპლიტუდების შესაბამისი მნიშვნელობები (1.22)-ის მიხედვით, მივიღებთ:
\(\dpi{120} \frac{F_{0}^{2}}{m^{2}A^{2}}=\left ( \omega _{0}^{2}-\omega ^{2} \right )^{2}+4\omega ^{2}\beta ^{2}\)
აქედან
| \(\dpi{120} A=\frac{F_{0}}{m\sqrt{\left ( \omega _{0}^{2}-\omega ^{2} \right )^{2}+4\omega ^{2}\beta ^{2}}}\) | (7.23) |
დამდგარი იძულებითი რხევების ამპლიტუდა პირდაპირპროპორციულია მაიძულებელი ძალის F0 ამპლიტუდისა, უკუპროპორციულია სისტემის m მასისა და მცირდება მილევის β კოეფიციენტის ზრდით. როცა F0, m და β მუდმივებია, ამპლიტუდა დამოკიდებულია მხოლოდ მაიძულებელი ძალის ციკლური ω სიხშირისა და სისტემის თავისუფალი არამილევადი რხევების ω0 სიხშირის თანაფარდობაზე. როცა მაიძულებელი ძალის ციკლური სიხშირე ω=0, მაშინ რცხევების ამპლიტუდა 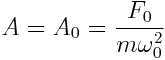 . ამ შემთხვევაში რხევები არ ხდება და წანაცვლება არის სტატიკური დეფორმაცია მუდმივი F0 ძალის გავლენით:
. ამ შემთხვევაში რხევები არ ხდება და წანაცვლება არის სტატიკური დეფორმაცია მუდმივი F0 ძალის გავლენით:
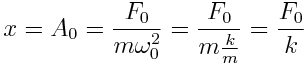
ამიტომ A0 გადახრას ხანდახან სტატიკურ ამპლიტუდას უწოდებენ.
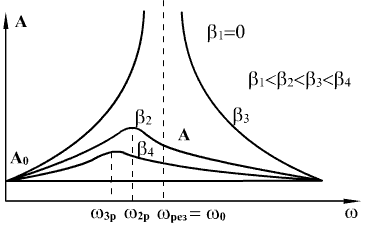
თუ არ არის დისიპაცია ანუ β=0, მაში რხევების ამპლიტუდა
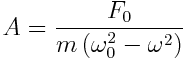
იზრდება მაიძულებელი Fdr ძალის ω ციკლური სიხშირის ზრდით და როცა ω=ω0 ხდება უსასრულოდ დიდი. ω ციკლური სიხშირის შემდგომი ზრდით იძულებითი რხევების А ამპლიტუდა მცირდება, ამასთან 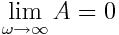 .
.
მაიძულებელი ω სიხშირის სისტემის ω0 საკუთარ სიხშირესთან მიახლოებისას იძულებითი რხევების ამპლიტუდის მკვეთრი ზრდის მოვლენას რეზონანსი ეწოდება.
თუ გვაქვს მილევა (β≠0), მაშინ იძულებითი რხევების ამპლიტუდა აღწევს მაქსიმალურ მნიშვნელობას, როცა (7.23) განტოლებაში მარჯვენა მხარის მნიშვნელი აღწევს მინიმუმს. გავუტოლოთ ნულს ფესქვეშა გამოსახულების ω-თი პირველი წარმოებული, მივიღებთ მისი მინიმუმის პირობას 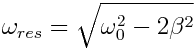 , სადაც ωres-ს უწოდებენ რეზონანსულ სიხშირეს. ωres აღნიშნავს ω ციკლური სიხშირის იმ მნიშვნელობას, რომლისთვისაც A=Amax.
, სადაც ωres-ს უწოდებენ რეზონანსულ სიხშირეს. ωres აღნიშნავს ω ციკლური სიხშირის იმ მნიშვნელობას, რომლისთვისაც A=Amax.
უკანასკნელი ფორმულიდან გამომდინარეობს, რომ კონსერვატული სისტემისთვის (β=0) ωres=ω0, ხოლო დისიპაციური სისტემისთვის ωres რამდენადმე ნაკლებია საკუთარ ციკლურ სიჩქარეზე. მილევის კოეფიციენტის გაზრდით რეზონანსის მოვლენა სულ ურო სუსტად ვლინდება და ბოლოს, როცა 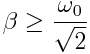 რეზონანსი სულაც ქრება.
რეზონანსი სულაც ქრება.
რეზონანსის მოვლენა გამოიყენება რხევების, მაგალითად ელექტრომაგნიტური რხევების გასაძლიერებლად. მეორეს მხრივ სხვადასხვა მანქანებისა და ნაგებობების კონსტრუირებისას უნდა გათვალისწინებული იქნას თუნდაც სულ მცირე პერიოდული ძალებიც კი, რათა თავიდან აცილებულ იქნას რეზონანსის არასასურველი შედეგები.