ვთქვათ K სისტემის x1 და x2 წერტილებში ერთდროულად მოხდა ორი ხდომილება დროის მომენტში t1=t2=t . ლორენცის გარდაქმნების თანახმად K’ სისტემაში ამ ხდომილებებს შეესატყვისება კოორდინატები
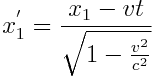 ;
; 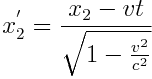
და დროის მომენტები
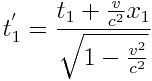 ; (1)
; (1)
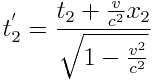 (2)
(2)
დაწერილი ფორმულებიდან ჩანს, რომ თუ ხდომილებები K სისტემაში ხდება ერთსადაიმავე ადგილას ანუ (x1 = x2), მაშინ ისინი K’ სისტემაშიც დაემთხვევიან სივრცულად (x'1 = x'2) და დროშიც (t'1 = t'2).
თუკი K სისტემაში ხდომილებები სივრცეში აცდენილია (x1 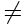 x2), მაშინ K’ სისტემაშიც ისინი იქნება სივრცულად აცდენილი. მაგრამ (t'2 - t'1) სხვაობის ნიშანი განისაზღვრება v (x2 - x1) ნიშნით. აქედან გამომდინარეობს, რომ სხვადასხვა K’ სისტემაში (სხვადასხვა v-ს დროს) (t'2 - t'1) სხვაობას შეიძლება ჰქონდეს სხვადასხვა სიდიდე და სხვადასხვა ნიშანი. ეს ნიშნავს, რომ ზოგ სისტემაში ხდომილება 1 წინ გაუსწრებს ხდომილება 2-ს, ზოგში კი პირიქით. ნათქვამი ეხება მხოლოდ ხდომილებებს, რომელთა შორის არ არის მიზეზშედეგობრივი კავშირი.
x2), მაშინ K’ სისტემაშიც ისინი იქნება სივრცულად აცდენილი. მაგრამ (t'2 - t'1) სხვაობის ნიშანი განისაზღვრება v (x2 - x1) ნიშნით. აქედან გამომდინარეობს, რომ სხვადასხვა K’ სისტემაში (სხვადასხვა v-ს დროს) (t'2 - t'1) სხვაობას შეიძლება ჰქონდეს სხვადასხვა სიდიდე და სხვადასხვა ნიშანი. ეს ნიშნავს, რომ ზოგ სისტემაში ხდომილება 1 წინ გაუსწრებს ხდომილება 2-ს, ზოგში კი პირიქით. ნათქვამი ეხება მხოლოდ ხდომილებებს, რომელთა შორის არ არის მიზეზშედეგობრივი კავშირი.
მიზეზშედეგობრივად დაკავშირებული ხდომილებები (მაგალითად, გასროლა და ტყვიის სამიზნეში მოხვედრა) არცერთ სისტემაში არ იქნება ერთდროული და ყველგან მიზეზი წინ უსწრებს შედეგს. ამის საჩვენებლად გამოვიყენოთ (1) და (2) და ვწერთ
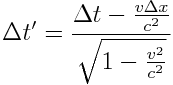
სადაც 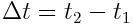 ,
, 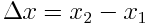 ხოლო
ხოლო 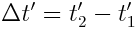
ვთქვათ 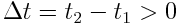 ისე, რომ ხდომილება 1 წინ უსწრებს ხდომილება 2-ს. მაშინ ჩვენ შეგვიძლია ვიპოვნოთ ისეთი დამკვირვებელი K’ სისტემაში, ვისთვისაც ∆t' < 0. ამისთვის საჭიროა
ისე, რომ ხდომილება 1 წინ უსწრებს ხდომილება 2-ს. მაშინ ჩვენ შეგვიძლია ვიპოვნოთ ისეთი დამკვირვებელი K’ სისტემაში, ვისთვისაც ∆t' < 0. ამისთვის საჭიროა
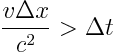
ანუ
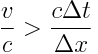
თუ  , მაშინ ხდომილებათა თანმიმდევრობა შეიძლება შებრუნდეს მხოლოდ თუ
, მაშინ ხდომილებათა თანმიმდევრობა შეიძლება შებრუნდეს მხოლოდ თუ 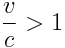 , რაც შეუძლებელია. სხვა სიტყვებით რომ ვთქვათ თუ სინათლის სხივს აქვს საკმარისი დრო გადაფაროს მანძილი მეტი ვიდრე სივრცული დისტანციაა ხდომილებებს შორის, მაშინ ასეთი ხდომილებების თანმიმდევრობის შებრუნება შეუძლებელია. მეორეს მხრივ თუ
, რაც შეუძლებელია. სხვა სიტყვებით რომ ვთქვათ თუ სინათლის სხივს აქვს საკმარისი დრო გადაფაროს მანძილი მეტი ვიდრე სივრცული დისტანციაა ხდომილებებს შორის, მაშინ ასეთი ხდომილებების თანმიმდევრობის შებრუნება შეუძლებელია. მეორეს მხრივ თუ 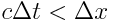 , მაშინ თვით სინათლიუს სიჩქარესაც არ შეუძლია დააკავშიროს ეს ორი ხდომილება ამ დროში და რათქმაუნდა ვერცერთი სხვა საშუალება ვერ მოახერხებს ამას და ამ შემთხვევაში ვერავითარი მიზეზშედეგობრივი კავშირი ვერ გვექნება. ამ შემთხვევაში შეიძლება მოიძებნოს დამკვირვებელი, რომლისთვისაც
, მაშინ თვით სინათლიუს სიჩქარესაც არ შეუძლია დააკავშიროს ეს ორი ხდომილება ამ დროში და რათქმაუნდა ვერცერთი სხვა საშუალება ვერ მოახერხებს ამას და ამ შემთხვევაში ვერავითარი მიზეზშედეგობრივი კავშირი ვერ გვექნება. ამ შემთხვევაში შეიძლება მოიძებნოს დამკვირვებელი, რომლისთვისაც  პირობებშიც იქნება ხდომილებების თანმიმდევრობა შებრუნებული.
პირობებშიც იქნება ხდომილებების თანმიმდევრობა შებრუნებული.
ეინშტეინის ფარდობითობის თეორიის პოსტულატებიდან გამომდინარე შეიძლება მოინახოს კანონები, რომლებიც ერთმანეთს აკავშირებს ერთმანეთისადმი წრფივად და თანაბრად მოძრავი ორი ათვლის სისტემის სივრცულ კოორდინატებსა და დროს.
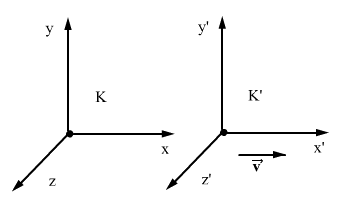
ამასთან არ გვაქვს არავითარი საფუძველი, ვიფიქროთ, რომ დრო K’ სისტემაში ემთხვევა დროს K სისტემაში, როგორც ეს უსიტყვოდ იგულისხმებოდა კლასიკურ ფიზიკაში. სიმარტივისთვის სიჩქარის მიმართულება ავარჩიოთ х და х’ ღერძების თანხვედრად. ვთქვათ t’ დროის მომენტში х’, у’, z’ კოორდინატების მქონე წერტილში ხდება რაღაც ფიზიკური პროცესი, რასაც დავარქვათ ხდომილება. ჩვენს ამოცანას წარმოადგენს K’ სისტემაში მომხდარი ხდომილების კოორდინატებისა და დროის х, y, z, t განსაზღვრა K სისტემაში.
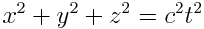
ანუ
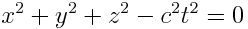 |
(6.1) |
რადგან, ეინშტეინის ფარდობითობის პრინციპის თანახმად, ელექტრომაგნიტური ტალღის გავრცელების კანონი და სიჩქარის სიდიდე ერთნაირია ყველა ინერციულ ათვლის სისტემაში, ამ განტოლებასთან ერთად სრულუფლებიანად შეგვიძლია დავწეროთ სფერული ტალღის განტოლება K’ სისტემაში
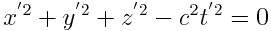
რადგან დროის საწყის მომენტში სისტემათა სათავეები ერთმანეთს ემთხვეოდა, ამიტომ
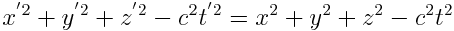 |
(6.2) |
კოორდინატებისა და დროის გარდაქმნის ფორმულები, პირველ რიგში, არ უნდა არღვევდნენ (6.1)და (6.2) თანაფარდობებს, ხოლო მეორე რიგში, უნდა იყოს წრფივი. წრფივობა გამომდინარეობს სივრცის ერთგვაროვნებისგან. რადგან K’ სისტემის მოძრაობა ხდება მხოლოდ х ღერძის გასწვრივ, ამიტომ у და z კოორდინატების გარდაქნის ფორმულებს ექნება სახე
y'=y, z'=z
х’ კოორდინატის х-ით გარდაქმნის კანონი შეიძლება ჩავწეროთ, გამომდინარე შემდეგი მოსაზრებიდან: თუ t=0 მომენტში K და K’ სისტემების სათავეები ერთმანეთს ემთხვეოდა, მაშინ х’ სიბრტყის კოორდინატა K სისტემაში ჩაიწერება ასე х=νt. შესაბამისად, ყველაზე ზოგად შემთხვევაში შეიძლება დავწეროთ
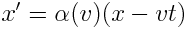 |
(6.3) |
სადაც კოეფიციენტი 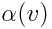 შეიძლება იყოს დამოკიდებული მხოლოდ ფარდობით სიჩქარეზე. ნუ გავაკეთებთ ნურავითარ დაშვებას ორ სისტემაში დროების დამთხვევაზე და შეგვიძლია წარმოვადგინოთ t’ როგორც წრფივი ფუნქცია х-სა და t -სი.
შეიძლება იყოს დამოკიდებული მხოლოდ ფარდობით სიჩქარეზე. ნუ გავაკეთებთ ნურავითარ დაშვებას ორ სისტემაში დროების დამთხვევაზე და შეგვიძლია წარმოვადგინოთ t’ როგორც წრფივი ფუნქცია х-სა და t -სი.
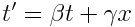 |
(6.4) |
ზოგადად 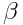 და
და 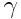 კოეფიციენტები შეიძლება იყოს დამოკიდებული v სიჩქარეზე. რომ აღმოჩენილიყო, რომ
კოეფიციენტები შეიძლება იყოს დამოკიდებული v სიჩქარეზე. რომ აღმოჩენილიყო, რომ 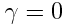 , ხოლო
, ხოლო 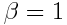 , მაშინ ჩვენ დავუბრუნდებოდით გალილეის გარდაქმნებს. \(\alpha\),
, მაშინ ჩვენ დავუბრუნდებოდით გალილეის გარდაქმნებს. \(\alpha\), 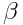 და
და 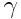 კოეფიციენტების განსაზღვრისთვის (6.3) და (6.4) უნდა ჩავსვათ (6.2)-ში. ეს გვაძლევს
კოეფიციენტების განსაზღვრისთვის (6.3) და (6.4) უნდა ჩავსვათ (6.2)-ში. ეს გვაძლევს
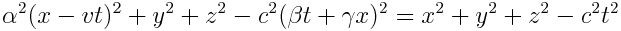
იგივეობის შესრულებისთის х2,t2და хt-ს შესაბამისი კოეფიციენტები ერთმანეთს გავუტოლოთ. ფრჩხილების გახსნით და შესაბამისი გარდაქმნების ჩატარებით მივიღებთ:
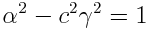
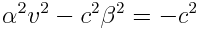
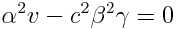
ამ სამი განტოლებიდან ვპოულობთ უცნობ სიდიდეებს \(\alpha\),  და
და  ,:
,:
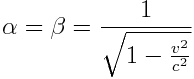
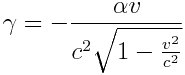
ამასთან ყველგან შევარჩიეთ ფესვების დადებითი ნიშნები. ჩავსვათ \(\alpha\), 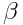 და
და 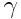 მნიშვნელობები (6.3)-სა და(6.4)-ში და გვექნება:
მნიშვნელობები (6.3)-სა და(6.4)-ში და გვექნება:
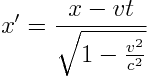 , , 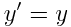 , , 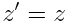 , , 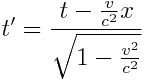 |
(6.5) |
ამ ფორმულებს ეწოდება ლორენცის გარდაქმნები. შტრიხიანიდან უშტრიხოზე პირუკუ გარდაქმნის ფორმულები ასეთია:
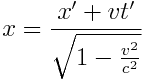 , , 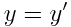 , , 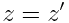 , , 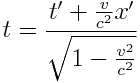 |
(6.6) |
ლორენცის გარდაქმნებს მივყევაღ დასკვნებამდე, რომლებიც ძირეულად უპირისპირდება სივრცესა და დროზე ჩვეულ შეხედულებებს.
უკვე ნიუტონის დინამიკაში ინერციით მოძრაობა მკვეთრად არის გამოყოფილი ყველა სხვა ტიპის მოძრაობათაგან. ნიუტონის პირველი კანონის პირდაპირ შედეგს წარმოადგენს იმის მტკიცება, რომ ყველა ინერციული დამკვირვებელი თანაბარია - იმ ხარისხით, რითაც სამართლიანია ნიუტონის პირველი კანონი. დამკვირვებლის თანაბრობა ვრცელდება ყველა სხვა მოძრაობის კანონზე და შესაბამისად ყველა სხვა მექანიკურ მოვლენაზე. ეინშტეინმა კი განავრცო ეს თანაბრობა საერთოდ ყველა მოვლენაზე, ჩამოაყალიბა რა ცნობილი პოსტულატები:
1. ყველა ფიზიკური კანონი ინვარიანტულია ათვლის ერთი ინერციული სისტემიდან მეორეში გადასვლისას.
2. სინათლის სიჩქარე ვაკუუმში ერთიდაიგივეა ათვლის ყველა სისტემაში და არ არის დამოკიდებული არც წყაროს მოძრაობის სიჩქარეზე და არც მიმღების მოძრაობის სიჩქარეზე.
ვარდნილ სხეულზე მოქმედებს ორი ძალა: სიმძიმის ძალა და ჰაერის წინააღმდეგობის ძალა. ამოცანის პირობის თანახმა ჰაერის წინააღმდეგობის ძალა შეიძლება გამოვსახოთ ასე: \(\vec{F}_{D}=-r\vec{v}\), სადაც r არის პროპორციულობის კოეფიციენტი, რომელიც დამოკიდებულია სხეულის ზომებზე, ფორმაზე და გარემოს თვისებებზე. სხეულის მოძრაობის განტოლება ვექტორული ფორმით იქნება:
\(m\frac{\mathrm{d} \vec{v}}{\mathrm{d} t}=m\vec{g}+\vec{F}_{D}\) (1)
დავაპროექტიროთ ეს განტოლება 0y ღერძზე, რომელიც მიმართულია ქვემოთ და ჩავწეროთ განტოლება (1) სკალარული ფორმით:
\(m\frac{\mathrm{d} v}{\mathrm{d} t}=mg-rv\)
ცვლადთა განცალების შემდეგ გვაქვს:
\(\frac{\mathrm{d}v}{mg-rv}=\frac{\mathrm{d}t}{m}\)
გავაინტეგროთ გამოსახულება და დავუსვათ ინტეგრირების საზღვრები, იმის გათვალისწინებით, რომ დროის 0-დან \(\tau\)-მდე ცვლილებისას სიჩქარე იცვლება 0-დან შემდგარი სიჩქარის ნახევრამდე :
\(\int_{0}^{\frac{u}{2}}\frac{\mathrm{d}v}{mg-rv}=\int_{0}^{\tau }\frac{\mathrm{d}t}{m}\) ;
\(-\frac{1}{r}\ln \left ( mg-rv \right ) | \right |_{0}^{\frac{u}{2}}=\frac{t}{m}| \right |_{0}^{\tau }\)
\(-\frac{1}{r}\ln \frac{mg-05ru}{mg}=\frac{\tau }{m}\).
უკანასკნელი გამოსახულებიდან მოვძებნოთ სასურველი დრო::
\(\tau =\frac{m}{r}\ln \left ( \frac{mg}{mg-05ru} \right )\), (2)
აქ შემავალი პროპორციულობის კოეფიციენტი r განვსაზღვროთ შემდეგი მოსაზრებების საშუალებით. შემდგარი სიჩქარის დროს სხეულზე მოქმედი სიმძიმის ძალისა და ჰაერის ხახუნის ძალების ტოლქმედი ნულის ტოლია, ამიტომ:
\(r=\frac{mg}{u}\) (3)
ჩავსვათ r-ის მნიშვნელობა (3)-დან გამოსახულება (2)-ში:
\(\tau =\frac{mu}{mg}\ln \left ( \frac{mg}{mg-05mg} \right )=\frac{u}{g}\ln 2\)
შეკვეცებისა და გამარტივების შემდეგ საბოლოოდ მივიღებთ:
\(\tau =\frac{u}{g}\ln 2\) (4)
ჩავსვათ რიცხვითი მნიშვნელობები (4)-ში და გამოვთვალოთ:
\(\tau\) = 2 5,7წმ.


