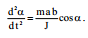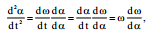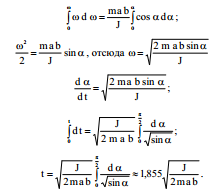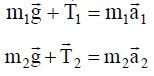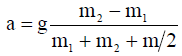სადაც \(\dpi{100} M=F_{in}b\cos \alpha\) – ინერციის ძალის მომენტია; J – კარის ინერციის მომენტია; 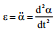
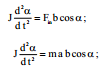
შევცვალოთ 
მაშინ განტოლება (2) მბს სახეს:
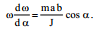
მოვახდინოთ ცვლადთა განცალება და (3) მიიღებს სახეს: 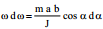
ახლა მოვახდინოთ ინტეგრირება ორჯერ:
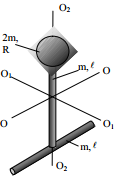
\(J_{1}=J_{sph}+J_{bar1}+J_{bar2}\), (1)
სადაც \(J_{sph},J_{bar1},J_{bar2}\) შესაბამისად არის სფეროსა და ვერტიკალური და ჰორიზონტალური ძელაკების ინერციის მომენტები ОО ღერძის მიმართ. ОО ღერძის მიმართ სფეროს ინერციის მომენტს ვპოულობთ შტეინერის თეორემის გამოყენებით: \(J_{sph}=J_{sph,c}+m_{sph}a^{2}=\frac{2}{5}m_{sph}R^{2}+m_{sph}a^{2}\)
სადაც \(J_{sph,c}\) არის სფეროს ინერციის მომენტი მის მასათა ცენტრზე გამავალი ღერძის მიმართ; msph=2m – სფეროს მასაა, ხოლო а არის მანძილი ღერძებს შორის. ჩვენ შემთხვევაში \(a=R+\frac{l}{2}=R+\frac{4R}{2}=3R\), მაშინ გვაქვს:
\(J_{sph}=\frac{4mR^{2}}{5}+2m(3R)^{2}=\frac{94}{5}mR^{2}\) (3)
ОО ღერძის მიმართ ვერტიკალური ძელაკის ინერციის მომენტი (ОО გადის ამ ძელაკის მასათა ცენტრზე) არის:
\(J_{bar1}=\frac{1}{12}m_{bar1}l^{2}=\frac{1}{12}m(4R)^{2}=\frac{4}{3}mR^{2}\) ,
ОО ღერძის მიმართ ჰორიზონტული ძელაკის ინერციის მომენტს ვიპოვით შტეინერის თეორემით, იმის გათვალისწინებით, რომ ძელაკი წვრილია და მისი მანძილი ОО ღერძამდე არის გადის ამ ძელაკის მასათა ცენტრზე) არის:\(\frac{l}{2}\):
\(J_{bar2}=m_{bar2}\left (\frac{l}{2} \right )^{2}=m(2R)^2=4mR^2\) (4)
ამდენად, ОО ღერძის მიმართ სისტემის ინერციის მომენტი ტოლია:
\(J_{1}=J_{sph}+J_{bar1}+J_{bar2}=\frac{94}{5}mR^{2}+\frac{4}{3}mR^{2}+4mR^{2}\) (5)
მსგავსი მსჯელობით მოვძებნით სისტემის ინერციის მომენტს О1 О1 ღერძის მიმართ:
\(T_{2}=T_{sph}+T_{bar1}+T_{bar2}=\)
\(=\frac{2}{5}m_{sph}R^{2}+m_{sph}(R+\frac{l}{2})+\frac{1}{12}m_{bar1}l^{2}+\frac{1}{12}m_{bar2}l^{2}+m_{bar2}\left (\frac{l}{2} \right )^{2}=\)
\(=\frac{4}{3}mR^{2}+2m9R^{2}+\frac{16}{12}mR^{2}+\frac{16}{12}mR^{2}+m4R^{2}=\frac{382}{15}mR^{2}\). (6) სისტემის O2O2 ღერძის მიმართ ინერციის მომენტის გამოთვლისას უნდა გავითვალისწინოთ, რომ ვერტიკალური ძელაკის ინერციის მომენტი O2O2 ღერძის მიმართ არის ნული:
\(T_{3}=T_{sph}+T_{bar1}+T_{bar2}=\frac{2}{5}m_{sph}R^{2}+\frac{1}{12}m_{bar2}l^{2}=\frac{32}{15}mR^{2}\)
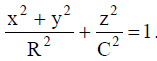
გადავწეროთ განტოლება (1) შემდეგნაირად:
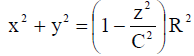
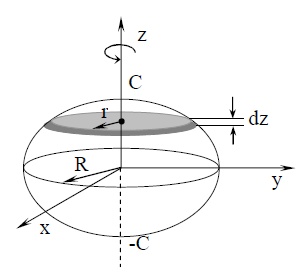
ცენტრიდან z მანძილზე აზრობრივად გამოვყოთ ელიფსოიდში dz უსასრულოდ მცირე სისქის მქონე დისკო. წარმოდგენილი დისკოს მასა ტოლია:
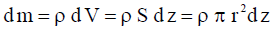
სადაც 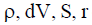
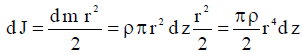
(2) ჩავსვათ (3)-ში და გავითვალისწინოთ, რომ 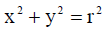
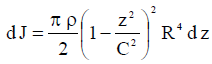
გავაინტეგროთ (4) და გამოვიყენოთ ბრუნვის ელიფსოიდის მოცულობის ფორმულა Vელ\(=\frac{4}{3}\pi R^{2}C\), მივიღებთ:

ჩავსვათ რიცხვითი მნიშვნელობები.
პასუხი: J= 0,004(კგ მ2).
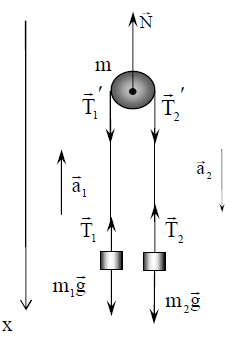
პირველი და მეორე ტვირთებისთვის ჩავწეროთ მოძრაობის განტოლებები ვექტორულად:
განვიხილოთ ამ განტოლებების პროექციები 0х ღერძზე. რადგან ძაფი უჭიმვადია, ამიტომ 
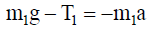
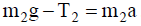
ჩვენგან ნახაზის პერპენდიკულარულად მიმართული 0z ღერძის მიმართ ორი ძალის მომენტის M1=T1'r და M2=T2'r მოქმედებით ჭოჭონაქი იძენს კუთხურ აჩქარებას 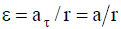
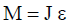
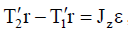
სადაც 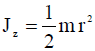
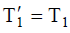
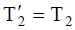
პასუხი: a=2,94 მ/წმ2 .