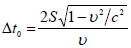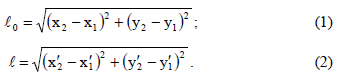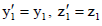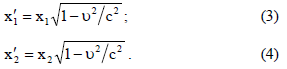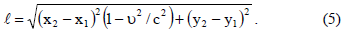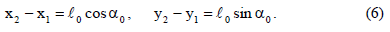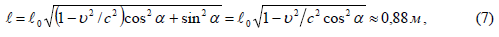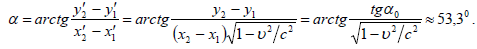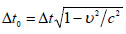მანძილი S, რომელსაც გაივლის კოსმოსური ხომალდი დედამიწასთან დაკავშირებულ ათვლის სისტემაში ტოლია S = 2,9 * 108 მ/წმ x 365 x 24 x 3600 \(\approx\) 3,8 *1017 მ. შესაბამისად დედამიწაზე მყოფი დამკვირვებლის საათით ხომალდის რენის ხანგრძლივობა იქნება \(\Delta t=2S/v\approx\) 83 წელი. კოსმოსურ ხომალდზე მყოფი საათის მიერ გაზომილი დროის ხანგრძლივობა დროის შენელების გათვალისწინებით იქნება  ანუ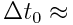

 213 წელი

 

ძელაკის სიგრძე დედამიწისა და რაკეტის სისტემებში ტოლია, შესაბამისად:

სიგრძის შეკვეცის ეფექტს ადგილი აქვს მხოლოდ მოძრაობის მიმართულებით. ლორენცის გარდაქმნებით 

(3)-ის და (4)-ის ჩასმით (2)-ში მივიღებთ:  https://yeapharmac..-100mg/

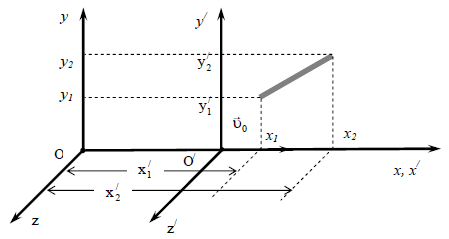
ნახაზიდან ჩანს, რომ:

მაშინ:

ხოლო მოსაძებნი კუთხისთვის გვაქვს:

ამოცანა 6.1

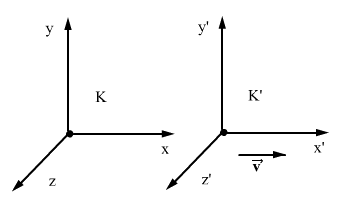
ათვლის სისტემა "რაკეტა" მოძრაობს ინერციული ათვლის სისტემის "დედამიწის" 0х ღერძის გასწვრივ მუდმივი 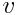 = 2*108 მ/წმ სიჩქარით. დედამიწის ათვლის სისტემაში მოთავსებულია 0х ღერძისადმი  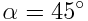კუთხით დახრილი  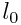=1 მ სიგრძის ძელაკი. ვიპოვნოთ ძელაკის სიგრძე და მისი დახრის კუთხე რაკეტის ათვლის სისტემის 0'х' ღერძის მიმართ. 0х და 0'х' ღერძები ურთიერთპარალელურებია.

ამოცანა 6.2

დედამიწიდან დამკვირვებლისთვის და რაკეტაში მჯდომი კოსმონავტისთვის რა დრო დასჭირდება დედამიწიდან 40 სინათლის წლით დაშორებულ ვარსკვლავამდე რაკეტის მიფრენას და უკან ჩამოვრენას თუ რაკეტის სიჩქარეა 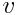 =2,9*108 მ/წმ ?

ამოცანა 6.3

К ათვლის სისტემაში ორი ერთნაირი საკუთარი 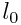  = 1 მ სიგრძის მქონე პარალელური ძელაკი მოძრაობს სიგრძის გასწვრივ ერთმანეთის შესახვედრად  ამ სისტემის მიმართ ტოლი 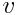= 2 *108 მ/წმ სიჩქარეებით. რისი ტოლია თითოეული ძელაკის სიგრძე მეორე ძელაკთან დაკავშირებულ სისტემაში?

ამოცანა 6.4

სხეულის მოძრაობისას მისი მოძრაობის გასწვრივი ზომები მცირდება n= 2 -ჯერ. რამდენჯერ იცვლება სხეულის მასა?

ამოცანა 6.5

5.5. მზის მასა ტოლია M =1,99 *1030 კგ. წლის განმავლობაში მზე ასხივებს E =12,6 *1023 ჯ ენერგიას. რამდენხანში განახევრდება მზის მასა?

ამოცანა 6.6

ელექტრონი მოძრაობს 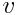= 0,9მ/წმ სიჩქარით. გამოთვალეთ პროცენტულად რა შეცდომა იქნება დაშვებული თუ ნაწილაკის კინეტიკურ ენერგიას კლასიკური მექანიკის ფორმულით გამოვთვლით.

ლორენცის გარდაქმნები

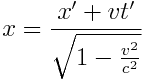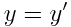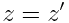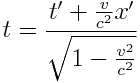  ,    ,     ,       (7.1)
 

ძელაკის სიგრძე l$</p> <table style= (7.2)
 

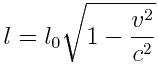
სხეულის საკუთარი დრო (უძრავ სისტემაში დროის შუალედი):

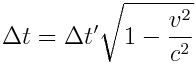(7.3)
 

სიჩქარეების შეკრების რელატივისტურ კანონი:

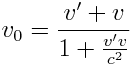(7.4)
 

სადაც 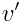  არის მოძრავი სხეულის სიჩქარე  სისტემის მიმართ, ხოლო  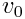კი უძრავი სისტემის მიმართ.

რელატივისტური იმპულსი:

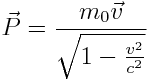(7.5)
 

რელატივისტური მასა:

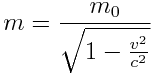(7.6)
 

ენერგია რელატივისტურ დინამიკაში:

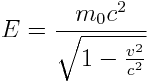(7.7)
 

უძრავი ნაწილაკის ენერგია:

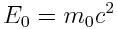(7.8)
 

კინეტიკური ენერგია:

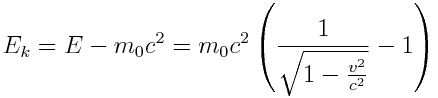(7.9)