რადგან სხეული დახრილ სიბრტყეზე მოძრაობს ხახუნის გარეშე, ამიტომ х ღერძის გასწვრივ აჩქარება მუდმივია და ტოლია:
რადგან სხეული დახრილ სიბრტყეზე მოძრაობს ხახუნის გარეშე, ამიტომ х ღერძის გასწვრივ აჩქარება მუდმივია და ტოლია:
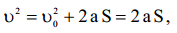 , სადაც
, სადაც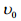 - სხეულის საწყისი სიჩქარეა, რაც პირობის თანახმად ნულია. ამდენად, (1)-ს გათვალისწინებით გვაქვს:
- სხეულის საწყისი სიჩქარეა, რაც პირობის თანახმად ნულია. ამდენად, (1)-ს გათვალისწინებით გვაქვს: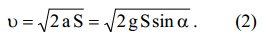
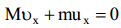 ანუ
ანუ 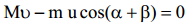 . აქედან, (2)-ის გათვალისწინებით, ტყვიის სიჩქარე ტოლი იქნება:
. აქედან, (2)-ის გათვალისწინებით, ტყვიის სიჩქარე ტოლი იქნება: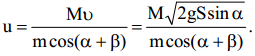
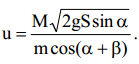
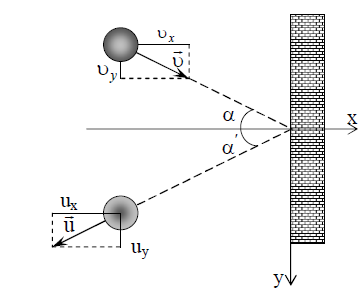 იმპულსისი შენახვის კანონის თანახმად:
იმპულსისი შენახვის კანონის თანახმად:\(m\vec{v}=m\vec{u}+\vec{p}\) (1)
განტოლება (1) ჩავწეროთ პროექციებში:

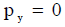 მაშინ გამოსახულება (3) მიიღებს სახეს:
მაშინ გამოსახულება (3) მიიღებს სახეს:
რადგან დაჯახება აბსოლუტურად დრეკადია, ამიტომ პროცესის დასრულებისთვის მექანიკური ენერგია (კინეტიკური) ინახება, მაგრამ რადგან კედელი მისი დიდი მასის გამო პრაქტიკულად უძრავი რჩება, ამიტომ მისი კინეტიკური ენერგია არის ნული, ე.ი. სრულდება ტოლობა:

(5)-დან გამოდის, რომ

(6) ჩავსვათ (4)-ში, მივიღებთ:

თუ (2)-ში გავითვალისწინებთ (6)-სა და (7)-ს, მივიღებთ:

პითაგორას თეორემით კედლის მიერ მიღებული იმპულსის მოდული, იმის გათვალისწინებით, რომ
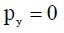 იქნება:
იქნება:
რიცხვითი მნიშვნელობების ჩასმით მივიღებთ: p = 5,2კგმ / წმ .
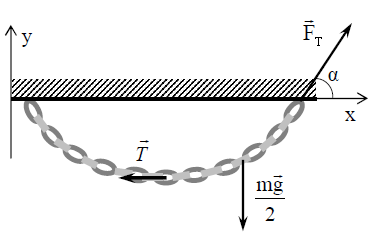
\(\vec{T}+\frac{m\vec{g}}{2}+\vec{F_{T}}=0\) (1)
x და y ღერძებზე პროექციებში, შესაბამისად, მივიღებთ:
х: \(-T+F_{T}\cos \alpha =0\) ანუ \(F_{T}\cos \alpha =T\) (2)
y: \(-\frac{mg}{2}+F_{T}\sin \alpha =0\) ანუ \(F_{T}\sin \alpha =\frac{mg}{2}\) (3)
(2) და (3) ავიყვანოთ კვადრატში და შევკრიბოთ, მივიღებთ:
\(F_{T}=\sqrt{T^{2}+\left ( \frac{mg}{2} \right )^{2}}\) (4)
(3) გავყოთ (2)-ზე, მივიღებთ
\(\alpha =\arctan \frac{mg}{2T}\) (5)
პასუხი: \(F_{T}=\sqrt{T^{2}+\left ( \frac{mg}{2} \right )^{2}}\) , \(\alpha =\arctan \frac{mg}{2T}\)
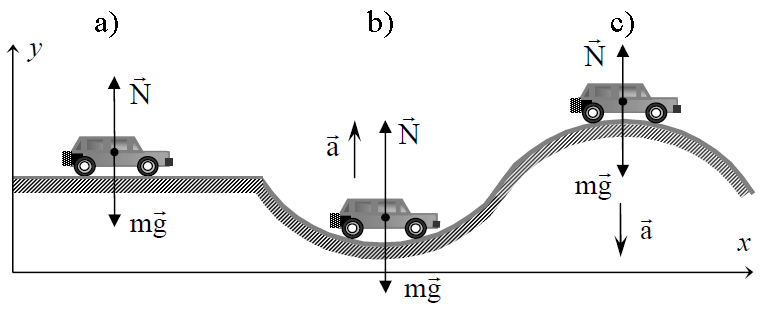
სამივე შემთხვევაში ავტომობილზე მოქმედებს ძალები: სიმძიმის ძალა და საყრდენის რეაქციის ძალა, რომლებიც ვერტიკალურად არიან მიმართულნი ურთიერთსაპირისპიროდ, ასევე მოტორის წევის ძალა და წინაღობის ძალა, რომლებიც მიმართულია ჰორიზონტულად.
მოძრაობის განტოლებას ვექტორულად აქვს შემდეგი სახე:
\(m\vec{g}+\vec{N}+\vec{F_{pl}}+\vec{F_{res}}=m\vec{a}\) (1)
განვიხილოთ თითოეული შემთხვევა:
a) როცა ავტომობილი მოძრაობს თანაბრად ჰორიზონტულ უბანზე, ის არ განიცდის აჩქარებას ვერტიკალური მიმართულებით, ამიტომ:
\(mg-N=0\) , ანუ \(N=mg\) .
ნიუტონის მესამე კანონის თანახმად ავტომობილი მოქმედებს გზაზე \(F_{pr}\) ძალით, რომელიც სიდიდით ტოლია \(N\)-ის და მის საპირიუსპიროდ არის მიმართული, ანუ:
\(F_{pr}=mg\) = 6860 ნ (2)
b) ჩაზნექილ უბანზე თანაბრად მოძრაობისას, ავტომობილი განიცდის ცენტრისკენულ აჩქარებას, რომლიც სიმრუდის რადიუსის გასწვრივ ცენტრისკენ არის მიმართული და მოძრაობის განტოლება (1) მიიღებს სახეს:
\(mg-N=m\tfrac{v^{2}}{R}\)
აქედან , ანალოგიით, მივიღებთ:
\(F_{pr}=m(g+\frac{v^{2}}{R})=\) 10360ნ (3)
c) კვლავ განიცდის ცენტრისკენულ აჩქარებას, რომელიც მიმართულია რადიუსის გასწვრივ სიმრუდის ცენტრისკენ. განტოლება (1) მიიღებს სახეს:
\(N-mg=m\tfrac{v^{2}}{R}\)
აქედან, წინა შემთხვევის აანალოგიურად, მივიღებთ:
\(F_{pr}=m(g-\frac{v^{2}}{R})=\) 10360 ნ (4)