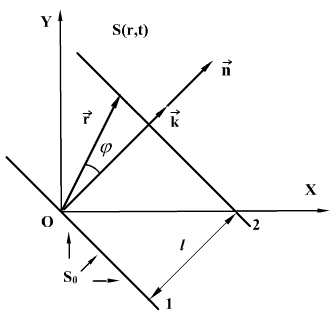
მივიღოთ განტოლება ბრტყელი ტალღისა, რომელიც ვრცელდება მიმართულებით, რაც х, у, z ღერძებთან ადგენს კუთხეებს α, β, γ. კოორდინატთა სათავეზე გამავალ სიბრტყეში რხევებს ჰქონდეს სახე 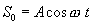 .
.
ავიღოთ ტალღური ზედაპირი (სიბრტყე), რომელიც კოორდინატთა სათავისგან დაშორებულია l-ით. ამ სიბრტყეში რხევები О წერტილში რხევისგან ჩამორჩება 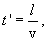 დროით, მაშინ ტალღის განტოლება
დროით, მაშინ ტალღის განტოლება
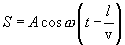 |
(8.4) |
გამოვსახოთ l დაშორება განსახილველი ზედაპირის წერტილების 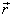 რადიუს-ვექტორით. ამისთვის შემოვიტანოთ ერთეულოვანი ვექტორი
რადიუს-ვექტორით. ამისთვის შემოვიტანოთ ერთეულოვანი ვექტორი 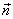 , რომელიც ტალური ზედაპირის ნორმალს წარმოადგენს. სკალარული ნამრავლი
, რომელიც ტალური ზედაპირის ნორმალს წარმოადგენს. სკალარული ნამრავლი
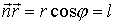
ჩავსვათ l-ის მნიშვნელობა (8.4) განტოლებაში და ომეგა შევიტანოთ ფრჩხილებში
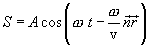
ფარდობა  ტოლია k ტალღური რიცხვისა. ვექტორს
ტოლია k ტალღური რიცხვისა. ვექტორს 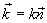 , რომელიც მოდულით ტოლია ტალღური რიცხვისა
, რომელიც მოდულით ტოლია ტალღური რიცხვისა 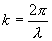 და მიმართულია ტალღური ზედაპირის ნორმალის გასწვრივ, ეწოდება ტალღური ვექტორი.
და მიმართულია ტალღური ზედაპირის ნორმალის გასწვრივ, ეწოდება ტალღური ვექტორი. 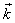 ვექტორის შემოღებით მივიღებთ
ვექტორის შემოღებით მივიღებთ
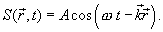 . . |
(8.5) |
რათა გადავიდეთ წერტილის რადიუს-ვექტორიდან მის კოორდინატებზე х, у, z , გამოვსახოთ სკალარული ნამრავლი 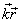 საკოორდინატო ღერძებზე ვექტორების პროექციებით :
საკოორდინატო ღერძებზე ვექტორების პროექციებით :
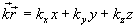
მაშინ ბრტყელი ტალღის განტოლება მიიღებს სახეს:
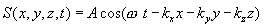 |
(8.6) |
სადაც 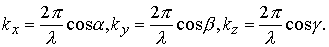
ერთ ფაზაში მერხევ წერტილთა გეომეტრიულ ადგილს ტალღური ზედაპირი ეწოდება. ტალღის ზედაპირს, რომელიც გამოყოფს სივრცის ნაწილს, სადაც ადგილი აქვს რხევებს, სივრცისგან სადაც რხევები ჯერ არ არის, ტალღის ფრონტი ეწოდება. სწორედ ფრონტი გადაადგილედება ფაზური სიჩქარის ტოლი სიჩქარით. ერთგანზომილებიანი სინუსოიდური ტალღის შემთხვევაში ტალღური ზედაპირის განტოლებას აქვს სახე:
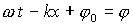
ამ პირობას დროის ყოველ მომენტში აკმაყოფილებს ОХ ღერძის ერთადერთი წერტილი, რომლის კოორდინატი х ტოლია:
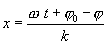
ტალღის φ ფაზის სზვადასხვა მნიშვნელობებს სხვადასხვა ტალღური ზედაპირები შეესაბამება, თითოეული მათგანი ერთგანზომილებიან ტალღის შემთხვევაში გადაგვარდება წერტილად. უკანასკნელი ფორმულიდან ჩანს, რომ ტალღური ზედაპირები დროთა განმავლობაში გარემოში გადაადგილდება სიჩქარით, რომელიც ტოლია 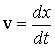 , ანუ ფაზური სიჩქარით, რომელიც ტოლია
, ანუ ფაზური სიჩქარით, რომელიც ტოლია
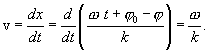 .
.
ამდენად, სინუსოიდური ტალღისთის მუდმივი ფაზის ზედაპირის გავრცელების სიჩქარე ემთხვევა ტალღის გავრცელების სიჩქარეს.
დავაფიქსიროთ (2.2) განტოლებაში ფაზის რაიმე მნიშვნელობა იყოს მუდმივი ამ წერტილისთვის
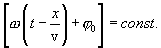
ეს გამოსახულება გვაძლევს კავშირს t დროსა და х კოორდინატს შორის, რომელშიც მოხდა დროის მოცემულ მომენტში ფაზის დაფიქსირება. 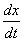 -ის განსაზღვრით ჩვენ ვიპოვნით სიჩქარეს, რომლითაც გადაადგილდება ფაზის მოცემული მნიშვნელობა. ამ თანაფარდობის გაწარმოებით მივიღებთ
-ის განსაზღვრით ჩვენ ვიპოვნით სიჩქარეს, რომლითაც გადაადგილდება ფაზის მოცემული მნიშვნელობა. ამ თანაფარდობის გაწარმოებით მივიღებთ
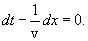
საიდანაც 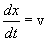
ამდენად, განტოლება (2.2)-ში ტალღის გავრცელების V სიჩქარე არის ფაზის გადანაცვლების სიჩქარე, ამიტომ მას ფაზურ სიჩქარეს უწოდებენ.
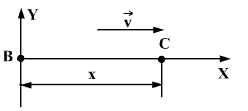
შევადგინოთ განტოლება, რომელიც საშუალებას იძლევა მოიძებნოს ტალღის ნებისმიერი წერტილის წანაცვლება დროის ნებისმიერ მომენტში. ვთქვათ В წერტილში არის რხევების წყარო. ტალღები v სიჩქარით ვრცელდება წყაროდან წრფის გასწვრივ.
В წერტილის რხევის განტოლება დავწეროთ ასე: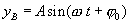
В-ს მარჯვნივ ყველა წერტილი, მაგალითად წერტილი С, იმეორებს В წერტილის მოძრაობას გარკვეული დაგვიანებით. დავწეროთ С წერტილის რხევის განტოლება. თუ В წერტილი ირხევა t დროის განმავლობაში, მაშინ რხევები მიაღწევს С წერტილს t' დროის შემდეგ, ამიტომ С წერტილის რხევის დრო ნაკლები იქნება t-ზე და შეადგენს t-t'. მაშინ С წერტილის რხევის განტოლება იქნება:
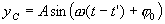
მანძილს В წერტილიდან С წერტილამდე,რომელიც ტოლია х-ის, ტალრა გადის სიჩქარით v=x/t' , საიდანაც t'=x/v. t'-ს გათვალისწინებით ტალღის განტოლება იქნება:
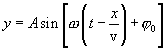 |
(8.2) |
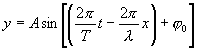 |
სადაც λ არის ტალღის სიგრძე.
აღვნიშნოთ k=2π/λ. ამ სიდიდეს ეწოდება ტალღური რიცხვი. ახლა მივიღებთ
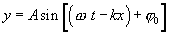 |
(8.3) |
ამ განტოლებას ეწოდება ბრტყელი ერთგანზომილებიანი ტალღის განტოლება და განსაზღვრავს გარემოს, გამომსხივლებლიდან x მანძილით დაშორებული, ნებისმიერი წერტილის წანაცვლებას მოცემულ მომენტში. სიდიდეს
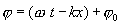
ეწოდება ტალღის ფაზა.