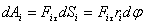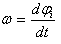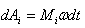ვთქვათ K’ სისტემის მიმართ უძრავ х’ წერტილში ხდება 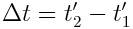 ხანგრძლივობის მოვლენა. მოვლენის სწყისს ამ სისტემაში შეესაბამება x'1=х’ წერტილი და t'1 დროის მომენტი, დასასრულს კი  x'2=х’ წერტილი და t'2 დროის მომენტი. K სისტემის მიმართ წერტილი, რომელშიც ხდება მოვლენა, გადაადგილდება. ლორენცის გარდაქმნის თანახმად:

 ; 

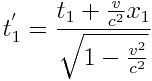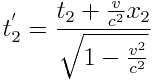
აქედან

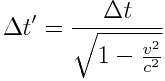
ანუ

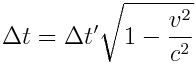
სხეულთან ერთად მოძრავი საათით ათვლილ \(\Delta t\) დროს უწოდებენ სხეულის საკუთარ დროს. როგორც ჩანს საკუთარი დრო ყოველთვის ნაკლებია, ვიდრე დრო, რომელიც აითვლება სხეულის მიმართ მოძრავი საათით. დროის შენელების რელატივისტური ეფექტი პრინციპში შესაძლებელს ხდის "მომავალში მოგზაურობას" (და არა წარსულში). მართლაც, ვთქვათ კოსმოსური ხომალდი, რომელიც მოძრაობს 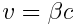 სიჩქარით (სადაც 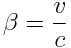) დედამიწის მიმართ, გდაფრინდა დედამიწიდან რომელიმე ვარსკვლავზე და გადმოფრინდა უკან. თუ სინათლე სინათლის სხივი ვარსკვლავიდან დედამიწამდე  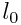მანძილს გადის  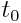დროში, მაშინ  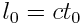დედამიწის დამკვირვებლისთვის ფრენის ხანგრძლივობა იქნება:

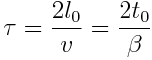
სწორედ ამდენით დაბერდებიან ადამიანები დედამიწაზე ხომალდის დაბრუნების მომენტისთვის. მეორეს მხრივ, კოსმოსურ ხომალდზე დაყენებული საათის მიხედვით, ფრენას დასჭირდება ნაკლები დრო, რომელიც ტოლია:

ფარდობითობის პრინციპიდან გამომდინარე ხომალდზე ყველა პროცესი (მათ შორის კოსმონავტების დაბერების პროცესიც) მიდის ზუსტად ისე, როგორც დედამიწაზე, მაგრამ არა დედამიწის საათით, არამედ ხომალდზე მდებარე საათით. ვთქვათ, მაგალითად 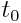=500წელს და 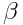=0,9999. მაშინ 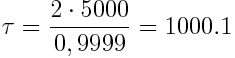წელი, ხოლო  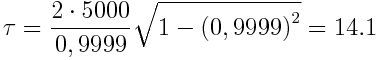წელი

განვიხილოთ х ღერძის გასწვრივ ძელაკი, რომელიც K’ ათვლის სისტემის მიმართ არის უძრავი. ამ სისტემაში მისი სიგრძე არის 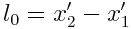 , სადაც х'1 და х'2 არის ძელაკის ბოლოების კოორდინატები და არ იცვლება t' დროსთან ერთად. K სისტემის მიმართ ძელაკი მოძრაობს v სიჩქარით. ამ სისტემაში ძელაკის სიგრძის მოსაძებნად უნდა მოინიშნოს მისი ბოლოების х'1 და х'2 კოორდინატები ერთსა და იმავე დროის მომენტში t1=t2=t. მათი სხვაობა  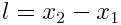მოგვცემს ძელაკის სიგრძეს, გაზომილს K სისტემაში. ლორენცის გარდაქმნების თანახმად

 ;  

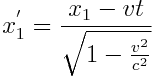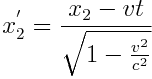
საიდანაც

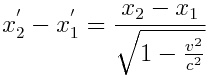
ანუ, საბოლოოდ

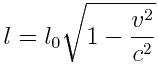
აამდენად, ძელაკის სიგრძე \(l\), გაზომილი იმ სისტემაში, რომლის მიმართაც ის მოძრაობს, გამოდის ნაკლები 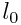 სიგრძეზე, რომელიც გაზომილია სისტემაში, რომლის მიმართაც ის უძრავია. ამ მოვლენას ლორენცის შეკვეცა ეწოდება.

სიჩქარეებს, რომელთა შემთხვევაშიც მოძრავი მატერიალური სხეულების ზომების შეკვეცა ხდება შესამჩნევი, ეწოდება რელატივისტური სიჩქარეები და დღესდღეობით ისინი მიიღწევა მსხვილ მასშტაბებში ლაბორატორიულ პრაქტიკასა და თანამედროვე საწარმოო აპარატებში.

ამოცანა 5.1

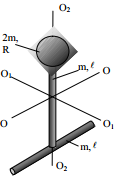
m = 80 გრ მასის სრული (სავსე)  დისკის ტიპის ჭოჭონაქზე გადადებულია წვრილი, უჭიმვადი, მოქნილი და უწონო ძაფი, რომლის ბოლოებზეც ჩამოკიდებულია ტვირთები მასებით m1 = 100 გრ და m2 = 200 გრ. რა აჩქარებით იმოძრავებენ ტვირთები, თუ მათ ნებაზე მივუშვებთ? ჭოჭონაქის ღერძის ხახუნი უგულებელვყოთ.

 

ამოცანა 5.2

განვსაზღვროთ m = 1 კგ მასისა და R = 10 სმ რადიუსის სავსე ბრუნვის ელიფსოიდის ინერციის მომენტი იმ ღერძის მიმართ, რომელიც მასათა ცენტრზე გადის.

 

 

 

 

 

ამოცანა 5.3

OO, O1O1 , O2O2  ღერძების მიმართ განვსაზღვროთ ინერციის მომენტი სისტემისა, რომელიც შედგება ერთმანეთთან ხისტად მიერთებული msph= 2m მასის და R რადიუსის სფეროსა და ორი ერთნაირი m მასისა და \(l=\) 4R სიგრძის მქონე ძეაკისგან. სამივე ღერძის გადაკვეთის წერტილი იმყოფება ვერტიკალური ძელაკის შუაში.

 

 

 

 

ამოცანა 5.4

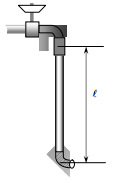
წყლის მილზე რეზინის მილაკით მიერთებულია \(l\) სიგრძის და  S განიკვეთის მინის მილი, რომელიც ბოლოში მართი კუთხით არის მოხრილი. განსაზღვრეთ რა კუთხით გადაიხრება ვერტიკალიდან მინის მილი, თუ მისგან წყლის გამოდინების სიჩქარე არის \(v\), ხოლო მინის მილის მასა mT..

 

 

 

 

ამოცანა 5.5

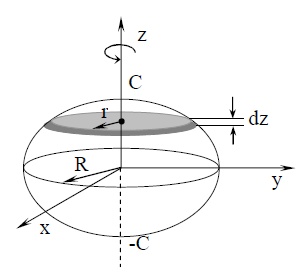
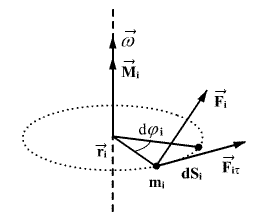ავტომობილი ადგილიდან იძვრის a აჩქარებით. ერთ-ერთი კარი, რომლის ინერციის მომენტი უძრავი ღერძის მიმართ არის J არის ღია და მისი სიბრტყე ავტომობილის ძარასთან ადგენს მართ კუთხეს. დროის რა მონაკვეთში დაიკეტება კარი. კარის მასათა ცენტრი b მანძილით არის დაშორებული ანჯამებიდან.
 
 

 

 

განვიხილოთ  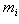მასის წერტილზე გარე  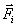ძალის მოქმედება.  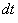 დროში ელემენტური მასა  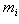გადის გზას  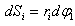 .  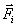ძალის მუშაობა ამ გზაზე ძალის პროექციით გადაადგილების მიმართულებაზე, რაც ცხადია უდრის ძალის ტანგენციალურ მდგენელს   .

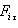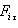
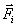
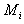
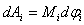
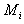
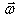
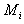
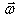
მაგრამ   ტოლია  ძალის  ბრუნვის ღერძის მიმართ  მომენტის მოდულისა. მუშაობა, და იქნება დადებითი თუ  -ს აქვს ისეთივე მიმართულება, როგორც   , და უარყოფითი თუ   და ვექტორების მიმართულებები ურთიერთსაპირისპიროა.

იმის გათვალისწინებით, რომ  

სხეულზე მოდებული ყველა ძალის მუშაობა

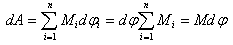(5.13)

სრული მუშაობა

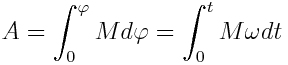(5.14)