\(F_{re}=\frac{\mathrm{d} \left (mv \right )}{\mathrm{d} t}\)

რადგან \(v=const\)

\(F_{re}=v\frac{\mathrm{d} m}{\mathrm{d} t}\)

რადგან \(m=\rho V\), სადაც \(\rho\) არის წყლის სიმკვრივე და მუდმივია, ხოლო \(V=Svt\), ამიტომ

\(F_{re}=S\rho v^{2}\)                                    (1)

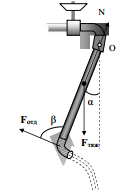
მინის მილზე მოქმედებს მის სიმძიმის ცენტრში მოდებული სიმძიმის ძალა, რომელიც შედგება თვითონ მილის სიმძიმის ძალისა და მასში მყოფი წყლის სიმძიმის ძალების ჯამისგან

\(F_{g}=(m_{T}+Sl\rho )g\)                      (2)

გადახრილი მილის წონასწორობა მოითხოვს, რომ სიმძიმის ძალისა და უკუცემის ძალების მომენტების ჯამი იყოს ნული:

\(M_{g}+M_{re}=0\)                             (3)

სიმძიმის ძალის მომენტი О ღერძის მიმართულების გათვალისწინებით:

\(M_{g}=-\frac{1}{2}F_{g}l\sin \alpha\)                   (4)

აქ  \(\frac{1}{2}l\sin \alpha\) არის О ღერძის მიმართ სიმძიმის ძალის მხარი.

უკუცემის ძალის მომენტი იქნება

\(M_{re}=F_{re}l\)                        (5)

ჩავსვათ (4) და (5) გამოსახულება (3)-ში:

\(F_{re}l=\frac{1}{2}F_{g}l\sin \alpha\)            (6)

ახლა ჩავსვათ (1) და (2) ბოლო (6) გამოსახულებაში და საბოლოოდ მივიღებთ:

\(\sin \alpha =\frac{2S\rho v^{2}}{\left ( m_{T}+Sl\rho \right )g}\).