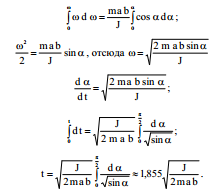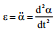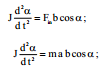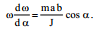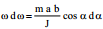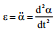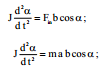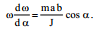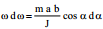მოძრაობის დაწყებიდან ავტომობილის კარი იწყებს დაკეტვას მასზე \(\dpi{100} \vec{F}_{in}=m\vec{a}\) ინერციის ძალის ზემოქმედებით. АВ აჩვენებს კარის მდგომარეობას საწყის მომენტში, АС – დროის t მომენტში, როცა კარი მობრუნდა α(t) კუთხით;\(\dpi{100} \vec{r}\) არის რადიუს-ვექტორი, გავლებული კარის ბრუნვის ღერძიდან კარის მასათა ცენტრამდე, ჩვენს შემთხვევაში იგი b-ს ტოლია ; \(\dpi{100} \vec{F}_{in}\) არის კარის მასათა ცენტრზე მოდებული ინერციის ძალა, \(\dpi{100} \beta\) კუთხეა რადიუს-ვექტორსა და ინერციის ძალას შორის. კარის მოძრაობა მიმდინარეობს ღერძის ირგვლივ, ანუ ადგილი აქვს ბრუნვით მოძრაობას ღერძის ირგვლივ, რომელიც პერპენდიკულარულია ნახაზისა და გადის А წერტილზე. ბრუნვითი მოძრაობის დინამიკის ძირითადი კანონის თანახმად გვაქვს: 
, (1)
სადაც \(\dpi{100} M=F_{in}b\cos \alpha\) – ინერციის ძალის მომენტია; J – კარის ინერციის მომენტია;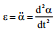 
– კუთხური აჩქარებაა. ზემოთქმულის გათვალისწინებით თანმიმდევრულად გარდავქმნათ (1):
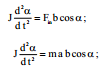; (2)
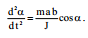
შევცვალოთ 
, და დროითი დიფერენცირებიდან კუთხით დიფერენცირებაზე:
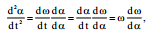
მაშინ განტოლება (2) მბს სახეს:
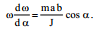. (3)
მოვახდინოთ ცვლადთა განცალება და (3) მიიღებს სახეს: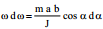 
.
ახლა მოვახდინოთ ინტეგრირება ორჯერ:
