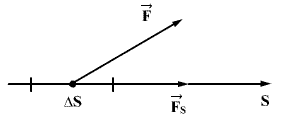
პოტენციური ველის ყოველ წერტილს შეესაბამება, ერთის მხრივ, სხეულზე მოქმედი 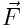 ძალის ვექტორის რაღაც მნიშვნელობა, მეორეს მხრივ,
ძალის ვექტორის რაღაც მნიშვნელობა, მეორეს მხრივ, 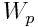 პოტენციური ენერგიის რაღაც მნიშვნელობა. ძალასა და პოტენციურ ენერგიას შორის უნდა არსებობდეს გარკვეული კავშირი.
პოტენციური ენერგიის რაღაც მნიშვნელობა. ძალასა და პოტენციურ ენერგიას შორის უნდა არსებობდეს გარკვეული კავშირი.
ამ კავშირის დასადგენად გამოვთვალოთ ელემენტარული მუშაობა, რომელსაც ველის ძალები ასრულებენ სხეულის მცირე 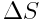 გადაადგილებაზე, რასაც ადგილი აქვს სივრცის ნებისმიერი S მიმართულები. ეს მუშაობა ტოლია
გადაადგილებაზე, რასაც ადგილი აქვს სივრცის ნებისმიერი S მიმართულები. ეს მუშაობა ტოლია
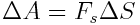
სადაც 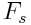 არის
არის 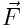 ძალის მდგენელი
ძალის მდგენელი ![]() მიმართულებაზე.
მიმართულებაზე.
რადგან მოცემულ შემთხვევაში მუშაობა სრულდება 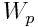 პოტენციური ენერგიის მარაგის ხარჯზე, ამიტომ იგი ტოლია
პოტენციური ენერგიის მარაგის ხარჯზე, ამიტომ იგი ტოლია 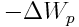 პოტენციური ენერგიის შემცირებისა
პოტენციური ენერგიის შემცირებისა 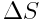 მონაკვეთზე:
მონაკვეთზე:
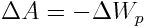
ორი ბოლო გამოსახულებიდან ვღებულობთ
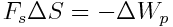
საიდანაც
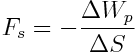
უკანასკნელი არის 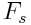 -ის საშუალო მნიშვნელობა
-ის საშუალო მნიშვნელობა 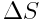 მონაკვეთზე. იმისათვის, რათა მივიღოთ
მონაკვეთზე. იმისათვის, რათა მივიღოთ 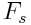 -ის მნიშვნელობა მოცემულ წერტილში უნდა მოვახდინოთ ზღვრული გადასვლა:
-ის მნიშვნელობა მოცემულ წერტილში უნდა მოვახდინოთ ზღვრული გადასვლა:
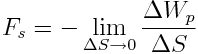
რადგან 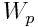 შეიძლება შეიცვალოს არა მარტო S ღერძის გასწვრივ გადაადგილებისას, არამედ სხვა მიმართულებებითაც, ამ სახით ზღვარი წარმოადგენს
შეიძლება შეიცვალოს არა მარტო S ღერძის გასწვრივ გადაადგილებისას, არამედ სხვა მიმართულებებითაც, ამ სახით ზღვარი წარმოადგენს 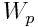 -ს ე.წ. კერძო წარმოებულს S-ით:
-ს ე.წ. კერძო წარმოებულს S-ით:
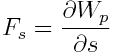
ეს თანაფარდობა სამართლიანია სივრცეში ნებისმიერი მიმართულებისთვის, კერძოდ დეკარტის კოორდინატთა სისტემის х, у, z ღერძების მიმართულებებისთვისაც:
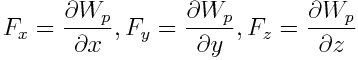
ეს ფორმულა განსაზღვრავს ძალის ვექტორის მდგენელებს კოორდინატთა ღერძებზე. თუ ცნობილია ეს მდგენელები, განისაზღვრება თვით ძალის ვექტორიც:
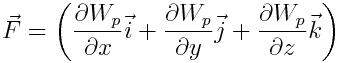
მათემატიკაში ვექტორს 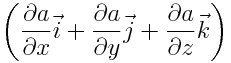 ,
,
სადაც а არის სკალარული ფუნქცია х, у და z კოორდინატებისა, ეწოდება ამ სკალარის გრადიენტი და აღინიშნება სიმბოლოთი 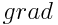 (a) ან
(a) ან  a. შესაბამისად ძალა ტოლია პოტენციური ენერგიის გრადიენტისა შებრუნებული ნიშნით
a. შესაბამისად ძალა ტოლია პოტენციური ენერგიის გრადიენტისა შებრუნებული ნიშნით
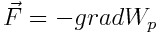 |
(4.15) |
განვიხილოთ დედამიწიდან h სიმაღლეზე აწეული სხეულის მდგომარეობის ცვლის პროცესი. მისი პოტენციური ენერგიაა
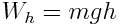
სხეულმა დაიწყო თავისუფალი ვარდნა (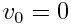 ). კინეტიკიდან ცნობილია, რომ დედამიწის ზედაპირის მიღწევისას მას ექნება სიჩქარე
). კინეტიკიდან ცნობილია, რომ დედამიწის ზედაპირის მიღწევისას მას ექნება სიჩქარე 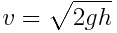 და კინეტიკური ენერგია:
და კინეტიკური ენერგია:
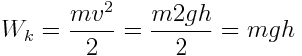
h სიმაღლიდან ჩამოვარდნილი სხეულის კინეტიკური ენერგია აღმოჩნდა მისი იმ პოტენციური ენერგიისა, რომელიც მას ჰქონდა ვარდნის დაწყებამდე. შესაბამისად:
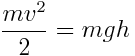
დედამიწის ზედაპირზე h=0 და პოტენციური ენერგია 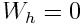 , ხოლო
, ხოლო 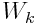 არის მაქსიმალური. ვარდნის დასაწყისში
არის მაქსიმალური. ვარდნის დასაწყისში 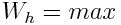 , ხოლო
, ხოლო 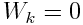 ანუ პოტენციური ენერგია გადადის (გარდაიქმნება) კინეტიკურში. ამდენად, სხეული-დედამიწის სისტემაში სხეულის ვარდნისას კინეტიკური ენერგია იზრდება და შესაბამისად მის
ანუ პოტენციური ენერგია გადადის (გარდაიქმნება) კინეტიკურში. ამდენად, სხეული-დედამიწის სისტემაში სხეულის ვარდნისას კინეტიკური ენერგია იზრდება და შესაბამისად მის 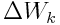 ცვლილებას, რომელიც ტოლია
ცვლილებას, რომელიც ტოლია 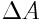 მუშაობისა, აქვს დადებითი ნიშანი, ანუ
მუშაობისა, აქვს დადებითი ნიშანი, ანუ
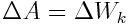 |
(4.12) |
პოტენციური ენერგია მცირდება და შესაბამისად მის ცვლილებას აქვს მინუს ნიშანი. ამიტომ შეიძლება ჩავწეროთ:
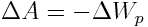 |
(4.13) |
შევკრიბოთ (4.12) და (4.13), მივიღებთ

ანუ 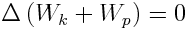
ჯამი 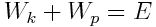 წარმოადგენს სრულ ენერგიას და შესაბამისად,
წარმოადგენს სრულ ენერგიას და შესაბამისად,
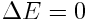 , ამიტომ
, ამიტომ
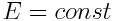 |
(4.14) |
ამდენად, ჩაკეტილი კონსერვატული სისტემის ენერგია რჩება მუდმივი მასში მიმდინარე ნებისმიერი პროცესებისა და გარდაქმნების დროს. ენერგია შეიძლება გადადიოდეს ერთი ფორმიდან სხვაში (მექანიკურში, სითბურში და ა.შ.), მაგრამ მისი სრული რაოდენობა რჩება მუდმივი. მოცემულ ცნებას უწოდებენ ენერგიის მუდმივობისა და გარდაქმნის კანონს.
პოტენციური ენერგია არის ენერგია, რომელიც განპირობებულია სხეულების ურთიერთგანლაგებით და მათი ურთიერთქმედების ხასიათით. შესაბამის პირობებში შესაძლებელია პოტენციური ენერგიის ცვლილება, რის გამოც სრულდება მუშაობა. m მასის სხეულის 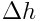 სიმაღლეზე ასაწევად აუცილებელია შესრულდეს მუშაობა მიზიდულობის Р ძალის წინააღმდეგ:
სიმაღლეზე ასაწევად აუცილებელია შესრულდეს მუშაობა მიზიდულობის Р ძალის წინააღმდეგ:
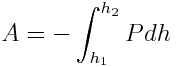 ,
,
ინტეგრალის წინ ნიშანი მინუსი არის იმიტომ, რომ Р ძალა მიმართულია h სიმაღლის ცვლილების საპირისპიროდ.
გავაინტეგროთ ეს გამოსახულება:
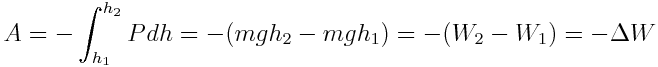
ეს ენერგია წავა სხეული-დედამიწის ჩაკეტილი სისტემის ენერგიის გაზრდაზე.
ჩავთვალოთ დედამიწის ზედაპირზე ![]() , მივიღებთ
, მივიღებთ
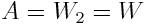
ეს W ენერგია არის სხეული-დედამიწის სისტემის ენერგია, როცა სხეული აწეულია h სიმაღლეზე და წარმოადგენს პოტენციურ ენერგიას:
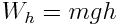 |
(4.11) |

 |
(4.6) |
სადაც 
გადავწეროთ (4.6) ასე
 |
(4.7) |
გავამრავლოთ განტოლება (4.7)  -ზე და გავაინტეგროთ წერტილი 1-დან წერტილ 2-მდე, მივიღებთ:
-ზე და გავაინტეგროთ წერტილი 1-დან წერტილ 2-მდე, მივიღებთ:
 |
(4.8) |
გავითვალისწინოთ, რომ  და გამოსახულება (4.8)-ის მარჯვენა მხარეს ინტეგრალი წარმოადგენს ყველა ძალის მუშაობას 1-2 უბანზე. მივიღებთ:
და გამოსახულება (4.8)-ის მარჯვენა მხარეს ინტეგრალი წარმოადგენს ყველა ძალის მუშაობას 1-2 უბანზე. მივიღებთ:
 |
(4.9) |
სიდიდეს
 |
(4.10) |
ეწოდება მატერიალური წერტილის კინეტიკური ენერგია. ამდაგვარად, მატერიალური წერტილის კინეტიკური ენერგია არის ენერგია, რომელიც აქვს ამ წერტილს მისი მოძრაობის შედეგად.
მიღებული (4.9) გამოსახულებიდან გამომდინარეობს, რომ 1-2 უბანზე მატერიალურ წერტილზე მოქმედი ყველა ძალის მუშაობა ამ უბანზე კინეტიკური ენერგიის ცვლილების ტოლია.