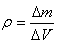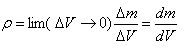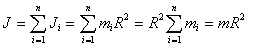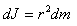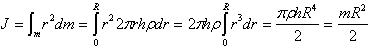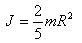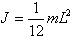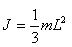(5.2) და (5.3) განტოლებების გათვალისწინებით, სხეულის ბრუნვის მომენტი 

(5.8)

ანუ

ეს გამოსახულება წარმოადგენს ნიუტონის მეორე კანონის ანალოგს მბრუნავი სხეულისთვის, საიდანაც გამომდინარეობს, რომ უძრავი ღერძის ირგვლივ ბრუნვისას მყარი სხეულის კუთხური აჩქარება  პირდაპირპროპორციულია ბრუნვის მომენტისა და უკუპროპორციულია ამ ღერძის მიმართ ინერციის მომენტისა. ამ გამოსახულებიდან გამომდინარეობს, რომ ინერციის მომენტი არის ინერციის ზომა უძრავი ღერძის მიმართ ბრუნვითი მოძრაობისას. გადატანითი მოძრაობისას, როგორც ცნობილია, ინერციის ზომა არის სხეულის მასა.

ხეულის ინერციის მომენტის საპოვნელად მისი შემადგენელი ყველა წერტილის ინერციის მომენტები უნდა ავჯამოთ

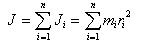(5.4)

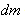
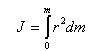ზოგადად, თუ სხეული უწყვეტია, იგი შედგება უსასრულოდ მცირე   მასის მქონე უამრავი წერტილისგან და სხეულის ინერციის მომენტი განისაზღვრება ინტეგრალით

(5.5)

სადაც r არის 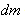 მანძილი ბრუნვის ღერძიდან.

სხეულის საზღვრებში მასის განაწილება შეიძლება დავახასიათოთ სიმკვრივის მეშვეობით

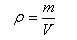(5.6)

სადაც m არის ერთგვაროვანი სხეულის მასა, V - მისი მოცულობა. არაერთგვაროვანი სხეულისთვის ეს ფორმულა იძლევა სიმკვრივის საშუალო მნიშვნელობას.

ამ შემთხვევაში მოცემულ წერტილში სიმკვრივე განისაზღვრება ასე

და მაშინ

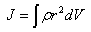(5.7)

ინტეგრირების საზღვრები დამოკიდებულია სხეულის ფორმებსა და ზომებზე. განტოლების ინტეგრირება ყველაზე ადვილია, როცა ბრუნვის ღერძი გადის სხეულის სიმძიმის ცენტრზე. განვიხილოთ ინტეგრირების შედეგები სხეულთა ყველაზე მარტივი  (გეომეტრიულად წესიერი) ფორმებისთვის, რომელთა მასები თანაბრად არის განაწილებული სხეულში.

ღრუ R რადიუსიანი ცილინდრი თხელი კედლებით.

თხელკედლებიანი ღრუ ცილინდრისთვის

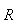
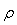
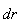
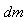
სავსე ერთგვაროვანი დისკი. ბრუნვის ღერძი არის დისკის ღერძი. რადიუსია , მასა m, სიმკვრე , დისკის სიმაღლე h. დისკის შიგნით ამოვჭრათ წარმოსახვითი ცილინდრი კედლის სისქით  და მასით .  მისთვის გვექნება

მთელი დისკი შეიძლება დავყოთ უსასრულო რაოდენობის ცილინდრებად და მერე ავჯამოთ:

ბირთვის ინერციის მომენტი სიმძიმის ცენტრზე გამავალი ბრუნვის ღერძის მიმართ.

L სიგრძისა და m მასის ლილვის ინერციის მომენტი ბრუნვის ღერძის მიმართ, რომელიც გადის:

а) ლილვის ცენტრზე - 

б) ლილვის საწყისზე - 

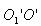
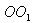
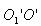
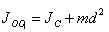შტეინერის თეორემა. გვაქვს სხეული, რომლის ინერციის მომენტი მასათა ცენტრზე გამავალი  ბრუნვის ღერძის მიმართ ცნობილია. უნდა განისაზღვროს ინერციის მომენტი ნებისმიერი  ღერძის მიმართ, რომელიც  ღერძის პარალელურია. შტეინერის თეორემის თანახმად, სხეულის ინერციის მომენტი ნებისმიერი ღერძის მიმართ ტოლია ამ ღერძის პარალელური ღერძის მიმართ მისი ინერციის მომენტის ჯამისა სხეულის მასისსა და ამ ღერძებს შორის მანძილის კვადრატის ნამრავლთან:

(5.7)

ნიუტონის მეორე კანონის თანახმად m მასის სხეულზე მოქმედი 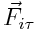 ძალის ტანგენციური მდგენელისთვისა და  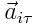 აჩქარებისათვის შეგვიძლია ჩავწეროთ

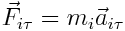
იმის გათვალისწინებით, რომ

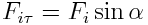 და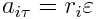   

გვექნება

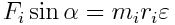
გავამრავლოთ მარცხენა და მარჯვენა მხარეები r_i-ზე და მივიღებთ

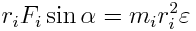(5.2)

ანუ

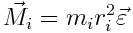
მატერიალური წერტილის 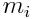 მასის ნამრავლს ბრუნვის ღერძიდან მისი მანძილის  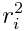კვადრატზე ეწოდება მატერიალური წერტილის ბრუნვის ღერძის მიმართ ინერციის მომენტი:

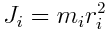(5.3)