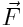ვთქვათ სხეულზე O1O2 ბრუნვის ღერძის პერპენდიკულარულ სიბრტყეში მოქმედებს  ძალა. დავშალოთ ეს ძალა ორ მდგენელად:  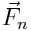და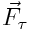 

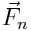 ძალა კვეთს ბრუნვის ღერძს და შესაბამისად არ მოქმედებს სხეულის ბრუნვაზე. 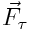მდგენელის მოქმედებით სხეული შეასრულებს ბრუნვით მოძრაობას O1O2 ღერძის გარშემო. ბრუნვის ღერძიდან  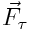ძალის მოქმედების წრფემდე r დაშორებას ეწოდება  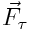ძალის მხარი. О წერტილის მიმართ ძალის მომენტი ეწოდება  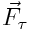ძალის ნამრავლს r ძალის მხარზე.

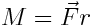
იმის გათვალისწინებით, რომ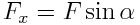  

ძალის მომენტი იქნება

.

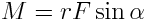ვექტორული ალგებრის მიხედვით ეს გამოსახულება წარმოადგენს 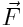 ძალის მოდების წერტილში გავლებული  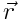რეადიუს ვექტორისა და ამ  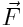ძალის ვექტორულ ნამრავლს. ამდენად, О წერტილის მიმართ ძალის მომენტი არის ვექტორული სიდიდე და ტოლია

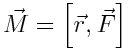(5.1)

ძალის მომენტის ვექტორი მიმართული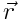ა  და 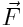-ზე გავლებული სიბრტყის პერპენდიკულარულად და მათთან ადგენს ვექტორთა მარჯვენა სამეულს (М ვექტორის თავიდან ჩანს, რომ ბრუნვა უმოკლესი მანძილით 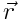-დან 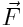-ისკენ ხდება საათის ისრის საწინააღმდეგოდ).

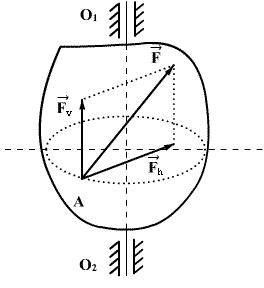
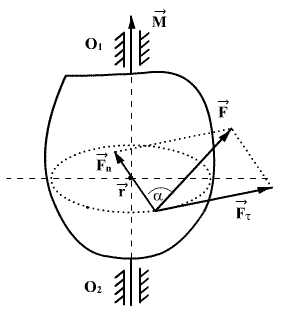
განვიხილოთ მოძრაობა მყარი სხზეულისა, რომელსაც აქვს O1O2 ბრუნვის ღერძი. ამ სხეულზე А წერტილში მოდებულია ნებისმიერად მიმართული 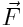 ძალა, რომელიც შეიძლება დავყოთ ვერტიკალურ და ჰორიზონტალურ მდგენელებად. ვერტიკალურმა მდგენელმა შეიძლება გამოიწვიოს სხეულის გადაადგილება ბრუნვის ღერძის მიმართულებით ამიტომ ბრუნვითი მოძრაობის განხილვისას ის შეიძლება გამოვრიცხოთ. ჰორიზონტული მდგენელი 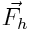, თუ ის არ გადაიკვეთება O1O2 ღერძთან იწვევს სხეულის ბრუნვას. ამ ძალის მოქმედება დამოკიდებულია მის რიცხვით მნიშვნელობაზე და ბრუნვის ღერძიდან მისი მოქმედების წრფის დაშორებაზე.

მატერიალური წერტილის გადატანითი მოძრაობის დინამიკაში კინემატიკურ სიდიდეებთან დამატებითად იქნა შემოღებული ძალისა და მასის ცნებები. ანალოგიურად, სხეულის ბრუნვითი მოძრაობის დინამიკის შესასწავლად, განხილული კინემატიკური მახასიათებლების გარდა, შემოდის ახალი სიდიდეები - ძალის მომენტი, ინერციის მომენტი და იმპულსის მომენტი.

მოცანა 4.1

განსაზღვრეთ 20 მ/წმ თანაბარი სიჩქარით მოძრავი m=700 კგ მასის ავტომობილის \(F_{pr}\) ნორმალური დაწოლა  გზაზე a) ჰორიზონტალურ უბანზე; b) ჩაზნექილი უბნის შუა ნაწილზე;  c) ამოზნექილი უბნის შუა ნაწილზე.  მრუდწირული უბნების სიმრუდის რადიუსია R=80მ.

ამოცანა 4.2

m მასის ჯაჭვი ორი ბოლოთი დაკიდებულია ერთ დონეზე. ამასთან ქვედა ცენტრალური რგოლი განიცდის T გაჭიმვის ძალას. განსაზღვრეთ ის α კუთხე, რომელსაც ჟაჭვი ადგენს ჰორიზონტთან დამაგრების წერტილებთან ახლოს და ამ წერტილებში \(F_{T}\) დაჭიმულობის ძალა. 

ამოცანა 4.3

\(v\)=10მ/წმ სიჩქარით მოძრავი m = 0,3 კგ მასის ბურთულა დრეკადად ეჯახება (აბსოლუტურად დრეკადი ეწოდება დაჯახებას, როცა დაჯახების შემდეგ სხეული ფორმას სრულად აღიდგენს ანუ, როცა მექანიკური ენერგია არ გადადის სხეულის შინაგან ენერგიაში) სწორ უძრავ კედელს ისე, რომ მისი სიჩქარე კედლის ნორმალთან ადგენს \(\alpha\)= 30° კუთხეს. განსაზღვრეთ კედლის მიერ მიღებული იმპულსი.

ამოცანა 4.4

ჰორიზონტისადმი α კუთხით დახრილ სიბრტყეზე  М მასის სხეული იწყებს ჩამოცურებას ხახუნის გარეშე. S მანძილის გავლის შემდეგ მას ხვდება m მასის მქონე ტყვია, რომლის სიჩქარე ჰორიზონტთან ადგენს \(\beta\) კუთხეს ზევიდან ქვევით და რჩება სხეულში. ამასთან ცხეული შეჩერდა. რა სიჩქარით მოფრინავდა ტყვია?

ამოცანა 4.5

m მასის ძელაკი ორი ჰორიზონტული ზეტაპირის შეერთების ადგილზე ძევს. რა მინიმალური მუშაობა უნდა შესრულდეს, რომ ძელაკი გაქაჩვით გადავწიოთ პირველი ზედაპირიდან მეორე ზედაპირზე, თუ ძელაკსა და ზედაპირებს შორის ხახუნის კოეფიციენტებია \(\mu _{1}\) და \(\mu _{2}\).

ამოცანა 4.6

 М = 2კგ მასის ბირთვი დრეკადად ეჯახება უძრავ  m = 1 კგ მასის ბირთვს. რა უდიდესი კუთხით შეიძლება გადაიხაროს დამჯახებელი ბირთვი თავისი პირვანდელი მოძრაობის მიმართულებიდან?

ამოცანა 4.7

m0 = 1,5კგ სასტარტო მასის მქონე რაკეტის მოდელი უძრაობიდან იწყებს მოძრაობას ვერტიკალურად ზევით და ამსთან უწყვეტად გამოისვრის აირის ჭავლს მის მიმართ მუდმივი სიჩქარით  u = 600მ/წმ. საწვავის ხარჯი არის μ = 0,3 კგ/წმ. განსაზღვრეთ, რა სიჩქარეს შეიძენს რაკეტა მოძრაობის დაწყებიდან 1 წმ-ის შემდეგ, თუ ის მოძრაობს: 1) გარე ძალების ზემოქმედების გარეშე; 2) სიმძიმის ძალის ერთგვაროვან ველში. შეაფასეთ ფარდობითი ცდომილება, როცა გარე ძალების ველის უგულებელყოფა ხდება.