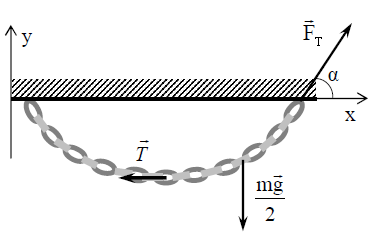
\(\vec{T}+\frac{m\vec{g}}{2}+\vec{F_{T}}=0\) (1)
x და y ღერძებზე პროექციებში, შესაბამისად, მივიღებთ:
х: \(-T+F_{T}\cos \alpha =0\) ანუ \(F_{T}\cos \alpha =T\) (2)
y: \(-\frac{mg}{2}+F_{T}\sin \alpha =0\) ანუ \(F_{T}\sin \alpha =\frac{mg}{2}\) (3)
(2) და (3) ავიყვანოთ კვადრატში და შევკრიბოთ, მივიღებთ:
\(F_{T}=\sqrt{T^{2}+\left ( \frac{mg}{2} \right )^{2}}\) (4)
(3) გავყოთ (2)-ზე, მივიღებთ
\(\alpha =\arctan \frac{mg}{2T}\) (5)
პასუხი: \(F_{T}=\sqrt{T^{2}+\left ( \frac{mg}{2} \right )^{2}}\) , \(\alpha =\arctan \frac{mg}{2T}\)