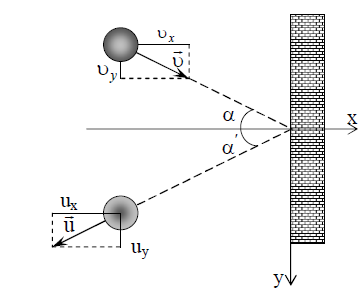
 იმპულსისი შენახვის კანონის თანახმად:
იმპულსისი შენახვის კანონის თანახმად:\(m\vec{v}=m\vec{u}+\vec{p}\) (1)
განტოლება (1) ჩავწეროთ პროექციებში:

რადგან კედლის ზედაპირი სწორია, ამიტომ y ღერძის მიმართულებით ბურთულა არ გადასცემს კედელს იმპოლსს, ანუ 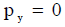 მაშინ გამოსახულება (3) მიიღებს სახეს:
მაშინ გამოსახულება (3) მიიღებს სახეს:

რადგან დაჯახება აბსოლუტურად დრეკადია, ამიტომ პროცესის დასრულებისთვის მექანიკური ენერგია (კინეტიკური) ინახება, მაგრამ რადგან კედელი მისი დიდი მასის გამო პრაქტიკულად უძრავი რჩება, ამიტომ მისი კინეტიკური ენერგია არის ნული, ე.ი. სრულდება ტოლობა:

(5)-დან გამოდის, რომ

(6) ჩავსვათ (4)-ში, მივიღებთ:

თუ (2)-ში გავითვალისწინებთ (6)-სა და (7)-ს, მივიღებთ:

პითაგორას თეორემით კედლის მიერ მიღებული იმპულსის მოდული, იმის გათვალისწინებით, რომ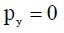 იქნება:
იქნება:

რიცხვითი მნიშვნელობების ჩასმით მივიღებთ: p = 5,2კგმ / წმ .
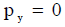 მაშინ გამოსახულება (3) მიიღებს სახეს:
მაშინ გამოსახულება (3) მიიღებს სახეს:
რადგან დაჯახება აბსოლუტურად დრეკადია, ამიტომ პროცესის დასრულებისთვის მექანიკური ენერგია (კინეტიკური) ინახება, მაგრამ რადგან კედელი მისი დიდი მასის გამო პრაქტიკულად უძრავი რჩება, ამიტომ მისი კინეტიკური ენერგია არის ნული, ე.ი. სრულდება ტოლობა:

(5)-დან გამოდის, რომ

(6) ჩავსვათ (4)-ში, მივიღებთ:

თუ (2)-ში გავითვალისწინებთ (6)-სა და (7)-ს, მივიღებთ:

პითაგორას თეორემით კედლის მიერ მიღებული იმპულსის მოდული, იმის გათვალისწინებით, რომ
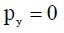 იქნება:
იქნება:
რიცხვითი მნიშვნელობების ჩასმით მივიღებთ: p = 5,2კგმ / წმ .