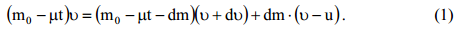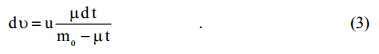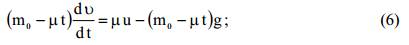1) გარე ძალების არარსებობის შემთხვევაში რაკეტას დროის რაღაც t მომენტში აქვს მასა 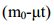
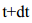
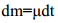
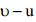
გარდავქმნათ განტოლება (1) და გავითვალისწინოთ 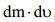
გავყოთ ამ გამოსახულების ორივე მხარე 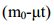
ამ გამოსახულების გაინტეგრირებით გვექნება
\(v_{1}=-uln(m_{0}-\mu t)+uln(m_{0})=uln(\frac{m_{0}}{m_{0}-\mu t})\)
2) ერთგვაროვან გრავიტაციულ ველში გარდა \(F=\mu u\) რეაქტიული ძალისა (იხ. განტ(2)) უნდა გავითვალისწინოთ სიმძიმის ძალა 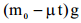
აქედან
\(\mathrm{d}v=\left ( \frac{\mu u}{m_{0}-\mu t}-g \right )\mathrm{d}t\) (7)
გავაინტეგროთ ეს გამოსახულება და მივიღებთ:
\(v_{2}=uln(\frac{m_{0}}{m_{0}-\mu t})-gt\) (8)
გარე ძალების ველის უგულებელყოფით გაკეთებული ფარდობითი ცდომილება ტოლია:
\(e=\frac{v_{1}-v_{2}}{v_{1}}=\frac{gt}{uln\frac{m_{0}}{m_{0}-\mu t}}\) (9)
ჩავსვათ ამოცანის მონაცემები ფორმულებში (5), (8) და (9), მივიღებთ:
\(v_{1}\)=134 მ / წმ ; \(v_{2}\) =124 მ / წმ ; e= 7,3%.