პერიოდული რხევა ეწოდება პროცესს, რომლის დროსაც სისტემა (მაგალითად, მექანიკური) ბრუნდება ერთდაიგივე მდგომარეობაში გარკვეული დროის შუალედის შემდეგ. დროის ამ შუალედს ეწოდება რხევის პერიოდი.

დამაბრუნებელი ძალა - ძალა, რომლის მოქმედებითაც მიმდინარეობს რხევის პროცესი. ეს ძალა ცდილობს სხეული ან მატერიალური წერტილი, რომელიც გადახრილია წონასწორობის მდგომარეობიდან, დააბრუნოს საწყის მდგომარეობაში.

მერხევ სხეულზე ზემოქმედების ხასიათის მიხედვით არჩევენ თავისუფალ (ანუ საკუთარ) რხევებსა და იძულებით რხევებს.

თავისუფალ რხევებს აქვს ადგილი, როცა მერხევ სხეულზე მოქმედებს მხოლოდ დამაბრუნებელი ძალა. იმ შემთხვევაში თუ არ ხდება ენერგიის გაბნევა, მაშინ თავისუფალი რხევები მიულევადია. თუმცა, რეალური რხევითი პროცესები მილევადია, რადგან მერხევ სისტემაზე მოქმედებს მოძრაობის წინაღობის ძალები (ძირითადად ხახუნი).

იძულებითი რხევები ხდება გარე პერიოდულად ცვლადი ძალის (რომელსაც მაიძულებელ ძალას უწოდებენ) ზემოქმედებით. ბევრ შემთხვევაში სისტემები ასრულებენ რხევებს, რომელთაც შეიძლება ჩაითვალოს ჰარმონიულად.

ჰარმონიული რხევები ეწოდება ისეთ რხევებს, რომელთა დროსაც წონასწორობის მდგომარეობიდან სხეულის გადახრა ხდება სინუსის ან კოსინუსის კანონით:

   ან    (7.1)

\(A\),  და  სიდიდეების ფიზიკური არსის საჩვენებლად განვიხილოთ წრეწირი და ვაბრუნოთ ОК რადიუსი კუთხური სიჩქარით საათის ისრის საწინააღმდეგოდ. თუ საწყის მომენტში ОК იყო ჰორიზონტულ სიბრტყეში, მაშინ t დროის შემდეგ ის შემობრუნდება  კუთხით. თუ საწყისი კუთხე განსხვავდება ნულისგან და ტოლია φ0-ის, მაშინ შემობრუნების კუთხე იქნება . ХО1 ღერძზე O'K' პროექცია ტოლია . ОК რადიუსის ბრუნვისას იცვლება პროექციის სიდიდე და K' წერტილი ასრულებს რხევას O' წერტილის მიმართ - ზევით, ქვევით და ა.შ. ამასთან х-ის მაქსიმალური მნიშვნელობა А-ს ტოლია და ეწოდება რხევის ამპლიტუდა; ω - წრიული ანუ ციკლური სიხშირე;  - რხევის ფაზა;  – საწყისი ფაზა. К წერტილის წრეწირზე ერთი შემობრუნებისას მისი პროექცია ასრულებს ერთ სრულ რხევას და ბრუნდება საწყის მდგომარეობაში.

პერიოდი Т ეწოდება ერთი სრული რხევის დროს. Т დროის ამოწურვის შემდეგ მეორდება რხევის მახასიათებელი ყველა ფიზიკური სიდიდის მნიშვნელობები. რხევის ერთი პერიოდის განმავლობაში წერტილი გადის გზას, რომელიც სიდიდით უდრის ოთხ ამპლიტუდას.

კუთხური სიჩქარე განისაზღვრება იმ პირობიდან, რომ Т პერიოდის განმავლობაში ОК რადიუსი ასრულებს ერთ ბრუნს, ანუ შემობრუნდება 2π რადიანი კუთხით:

 ანუ  

რხევის სიხშირე - ერთ წამში რხევათა რაოდენობა, ანუ რხევის სიხშირე განისაზღვრება როგორც პერიოდის შებრუნებული სიდიდე:

 ანუ  

აკუსტიკა, რადიოტექნიკა, ოპრიკა და მეცნიერებისა და ტექნიკის სხვა დარგები ეყრდნობა რხევებისა და ტალღების შესახებ ცოდნას. რხევების თეორია დიდ როლს თამაშობს მექანიკაში, განსაკუთრებით საფრენი აპარატების, ხიდების, სხვადასხვა ტიპის მანქანებისა და კვანძების სიმტკიცის გათვებში.

კლასიკური მექანიკის განტოლებები ინვარიანტულია გალილეის გარდაქმნის მიმართ, ხოლო ლორენცის გარდაქმნების მიმართ ისინი არ არიან ინვარიანტულნი. ფარდობითობის თეორიიდან გამომდინარეობს, რომ დინამიკის განტოლებას, რომელიც არის ინვარიანტული ლორენცის გარდაქმნების მიმართ, აქვს სახე:

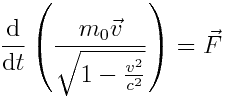
სადაც m0 - ინვარიანტულია, ანუ ერთნაირია ყველა ათვლის სისტემაში და ეწოდება ნაწილაკის უძრაობის მასა, \(\vec{v}\) არის ნაწილაკის სიჩქარე, \(\vec{F}\) არის ნაწილაკზე მოქმედი ძალა. შევადაროთ კლასიკურ განტოლებას

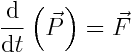
მივდივართ დასკვნამდე, რომ ნაწილაკის რელატივისტური იმპულსი ტოლია

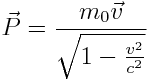(6.7)

 

რელატივისტური მასა.

განვსაზღვროთ ნაწილაკის m მასა როგორც პროპორციულობის კოეფიციენტი სიჩქარესა და იმპულსს შორის. მივიღებთ, რომ ნაწილაკის მასა დამოკიდებულია მის სიჩქარეზე.

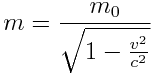(6.8)

 

ენერგია რელატივისტურ დინამიკაში.

ფარდობითობის თეორიაში ენერგიისთვის მიიღება გამოსახულება:

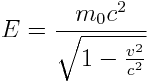(6.9)

(2.3)-დან გამოდის, რომ უძრავ ნაწილაკს აქვს ენერგია

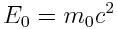(6.10)

ამ სიდიდეს ეწოდება ნაწილაკის უძრაობის ენერგია. კინეტიკური ენერგია, რათქმაუნდა, ტოლია

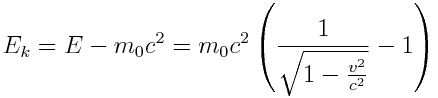(6.11)

მივიღებთ რა მხედველობაში, რომ 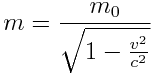 , ნაწილაკის სრული ენერგიის გამოსახულება შეიძლება ჩავწეროთ ასე

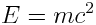(6.12)

უკანასკნელი გამოსახულებიდან გამოდის, რომ სხეულის ენერგია და მასა ყოველთვის ერთმანეთის პროპორციულებია. სხეულის ენერგიის ნებისმიერ 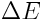 ცვლილებას თან ახლავს მისი მასის ცვლილება

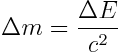
და პირიქით, მაისი ნებისმიერ 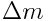 ცვლილებას თან ახლავს ენერგიის ცვლილება 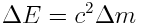. ამას ეწოდება მასისა და ენერგიის ურთიერთკავშირის ან პროპორციულობის კანონი.

ვთქვათ K’ სისტემაში მატერიალური წერტილი მოძრაობს х’ ღერძის გასწვრივ მუდმივი 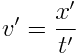 სიჩქარით. სისტემა K’ მოძრაობს K სისტემის მიმართ იგივე მიმართულებით \(v\) სიჩქარით. განვსაზღვროთ K სისტემის მიმართ მატერიალური წერტილის  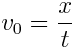სიჩქარე. ვთქვათ როცა t=t'=0, მატერიალური წერტილი იმყოფება კოორდინატთა სათავეში, ამასთან x=x'=0. K სისტემისთვის:

;  

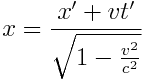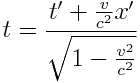
\(v_{0}\)-ის გამოსახულებაში ჩავსვათ x და t

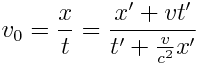
მრიცხველი და მნიშვნელი გავყოთ t-ზე

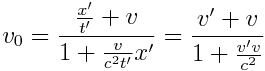
ეს გამოსახულება წარმოადგენს სიჩქარეების შეკრების რელატივისტურ კანონს. მცირე სიჩქარეების შემთხვევაში, როცა 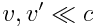 გვაქვს

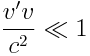 და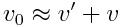 

ანუ სიჩქარეების შეკრების რელატივისტური კანონი გადადის კლასიკურში.