დრეკადი რხევის დროს დამაბრუნებელი ძალა F = -kx. თუ დრეკადის გარდა სხვა ძალა არ არის, რხევას უწოდებენ თავისუფალს. ნიუტონის მეორე კანონის თანახმად

,

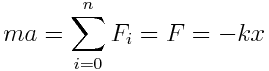ანუ

.

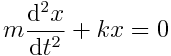გავყოთ ორივე შესაკრები m-ზე:

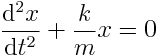(7.7)

ამ თანაფარდობას უწოდებენ ჰარმონიული თავისუფალი რხევის ძირითად განტოლებას. ამ განტოლების ზოგად ამონახსნს აქვს სახე

,

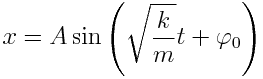ამაში ადვილად დავრწმუნდებით თუ ჩავსვამთ х-ს საწყის განტოლებაში.

კინეტიკური ენერგია:

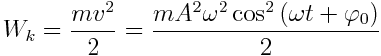(7.4)

პოტენციური ენერგია:

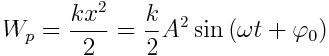
გავითვალისწინოთ, რომ 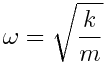  ანუ 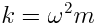 , უკანასკნელი გამოსახულება ასე შეიძლება ჩავწეროთ:

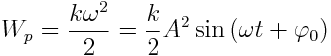(7.5)

მერხევი სხეულის სრული ენერგია ტოლია კინეტიკური და პოტენციური ენერგიების ჯამისა

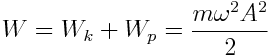(7.6)

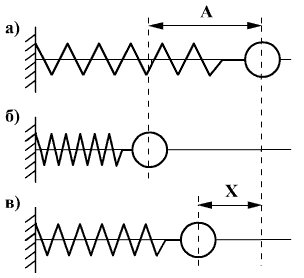
ზამბარიანი ქანქარა შედგება ჰორიზონტულ ძელაკზე დამაგრებული ზამბარისა და მასიური ბირთვისგან, რომელსაც შეუძლია ამ ძელაკზე სრიალი. ვთქვათ ზამბარაზე მიმაგრებულია გახვრეტილი ბირთვი, რომელიც სრიალებს მიმმართველი ღერძის გასწვრივ. ნახაზზე a) ნაჩვენებია უძრავი ბირთვის მდგომარეობა, ნახაზზე b) ნაჩვენებია ძამბარის მაქსიმალური შეკუმშვის მდგომარეობა, ხოლო ნახაზზე c) ნაჩვენებია ბირთვის ნებისმიერი მდებარეობა.

შეკუმშვის ძალის ტოლი დამაბრუნებელი ძალის მოქმედებით ბირთვი შეასრულებს რხევით მოძრაობას. შეკუმშვის ძალაა F = -kx , სადაც k არის ზამბარის სიხისტის კოეფიციენტი. ნიშანი მინუსი აჩვენებს, რომ ძალის მიმართულება და წანაცვლების მიმართულება ურთიერთსაპირისპიროა. დროის ნებისმიერ t მომენტში ქანქარის პოტენციური ენერგია იქნება

; 

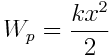ხოლო კინეტიკური

.

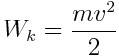იმისათვის, რათა გამოვიყვანოთ ბირთვის მოძრაობის განტოლება, უნდა დავაკავშიროთ х და t. გამოყვანა ეფუძნება ენერგიის მუდმივობის კანონს. სრული მექანიკური ენერგია ტოლია სისტემის კინეტიკური და პოტენციური ენერგიების ჯამის. მოცემულ შემთხვევაში:

 .

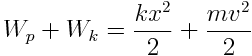მდგომარეობაში b) ,  :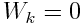

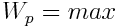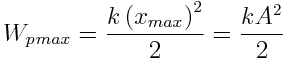
სადაც A=x_max

ენერგიის მუდმივობის გამო ვწერთ:

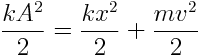
განვსაზღვროთ აქედან სიჩქარე:

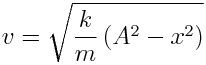
რადგან 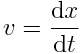, ამიტომ გვექნება

.

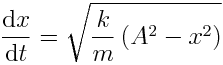მოვახდინოთ ცვლადთა განცალება

.

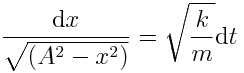ამ გამოსახულების ინტეგრირებით მივიღებთ:

 ,

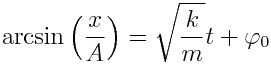სადაც 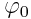 - ინტეგრირების მუდმივაა.

ბოლო გამოსახულებიდან გამოდის, რომ

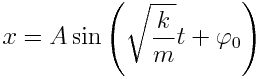(7.2)

შევადაროთ გამოსახულება (7.1) გამოსახულება (7.2)-ს, მივიღებთ

;

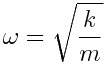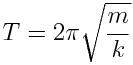(7.3)

ამდენად, დრეკადი ძალის მოქმედებით სხეული ასრულებს ჰარმონიულ რხევას. დრეკადისგან განსხვავებული ბუნების ძალებს, რომლებისთვისაც სრულდება პირობა F = -kx, ეწოდებათ კვაზიდრეკადი ძალები. ამ ძალების მოქმედებით სხეულები ასევე ასრულებენ ჰარმონიულ რხევებს. ამასთან გვაქვს:

წანაცვლება: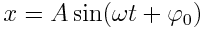
სიჩქარე: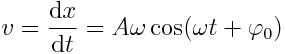
აჩქარება: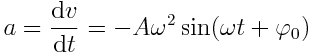