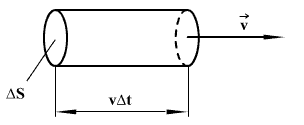
ენერგიის ნაკადის სიმკვრივის ვექტორის რიცხვითი მნიშვნელობა განისაზღვრება შემდეგნაირად:
 |
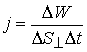(8.12) |
სადაც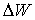 
არის ენერგია, რომელიც 
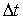დროში ენერგიის გადატანის მიმართულების პერპენდიკულარულ 
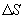ფართში გადააქვს ტალღას. სხვა სიტყვებით რომ ვთქვათ, ეს ვექტორი რიცხობრივად ტოლია სიმძლავრისა, რომელიც გადის გავრცელების პერპენდიკულარული ერთეულოვან ფართობში. 
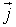ვექტორის მიმართულება ემთხვევა ტალღის ენერგიის გავრცელების მიმართულებას.
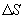ფართში 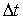დროში გავა 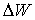ენერგია, რომელიც მოთავსებულია 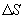ფუძისა და 
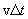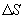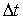(ტალღის ფაზური სიჩქარეა) სიმაღლის ცილინდრში. თუ ცილინდრის ზომები საკმაოდ მცირეა ( და სიმცირის გამო) იმისთვის რათა ცილინდრის ყველა წერტილში ენერგიის სიმკვრივე ჩაითვალოს ერთნაირად, მაშინ 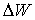შეიძლება მოიძებნოს როგორც w ენერგიის სიმკვრივისა და ცილინდრის მოცულობის ნამრავლი,
რაც ტოლია 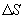v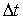 , მაშინ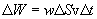 
ჩავსვათ ეს გამოსახულებები (8.12)-ში, მივირებთ
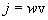
თუ განვიხილავთ v ფაზურ სიჩქარეს ვექტორად, რომელიც მიმართულია ტალღის გავრცელების (და ენერგიის გადატანის), შეიძლება დავწეროთ
 |
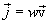(8.13) |
ამ სიდიდეს უწოდებენ ენერგიის ნაკადის სიმკვრივის ვექტორს.
ენერგიის ნაკადის სიმკვრივის ვექტორი, ისევე როგორც ენერგიის სიმკვრივე განსხვავებულია სივრცის სხვადასხვა წერტილში. მისი დროითი საშუალო ტოლია:
\(\fn_jvn \vec{j}_{m}=\vec{w}\vec{v}=\frac{1}{2}\rho A^{2}\omega ^{2}\vec{v}\)
დრეკად გარემოში ტალღის მოცულობითი სიმკვრივე (w), განისაზღვრება შემდეგნაირად:
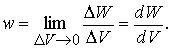
სადაც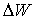 
ტალღის სრული მექანიკური ენერგიაა 
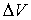მოცულობაში. (8.11)-დან გამოდის, რომ ბრტყელის სინუსოიდური ტალღების ენერგიის მოცულობითი სიმკვრივე არის
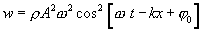
ამდენად, სივრცის უბანს, რომელიც მონაწილეობს ტალღურ პროცესში, აქვს ენერგიის დამატებითი მარაგი. ეს ენერგია მიეწოდება რხევების წყაროდან გარემოს სხვადასხვა წერტილებს თვით ტალღის მიერ, ანუ, ტალღას გადააქვს ენერგია.
ვიპოვნოთ დრეკადი გარემოს dV მცირე მოცულობის ენერგიის ცვლილება, დაკავშირებული გარემოში ბრტყელი ტალღის გავრცელებასთან, რომელიც მოცემულია განტოლებით
 |
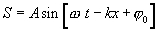(8.9) |
dV მოცულობის სიმცირის გამო შეიძლება ჩავთვალოთ, რომ მასში მოქცეული ყველა ნაწილაკი ირხევა ერთ ფაზაში, ასე რომ მათი სიჩქარეები ერთნაირია და ტოლია
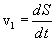
ამიტომ dV მოცულობის გარემოს კინეტიკური ენერგია, რომელიც დაკავშირებულია რხევით მოძრაობებთან, ტოლია
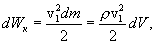
სადაც ρ გარემოს სიმკვრივეა. (8.9)-დან გამოდის
\(V_{1}=A\omega \cos \left [ \omega t-kx+\varphi _{0} \right ]\)
ამიტომ
 |
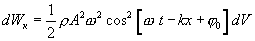(8.10) |
ტალღური მოძრაობისას dV მოცულობის დეფორმაციის (განივი ტალღის შემთხვევაში წანაცვლების დეფორმაცია, ხოლო გასწვრივი ტალღის შემთხვევაში მოცულობითი შეკუმშვა) მუშაობის გამოთვლა აჩვენებს, რომ dV მოცულობის გარემოს პოტენციური ენერგია dWp ტოლია მისი კინეტიკური ენერგიისა. დრეკადი გარემოს dV ელემენტარული მოცულობის რხევითი მოძრაობის სრული მექანიკური ენერგია ტოლია მისი კინეტიკური და პოტენციური ენერგიების ჯამისა.
 |
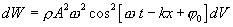(8.11) |
თითოეული ცვლადით ორჯერ გავაწარმოოთ განტოლება (8.6):
 |
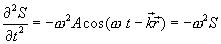(8.7) |
   |
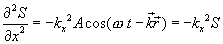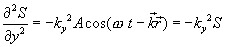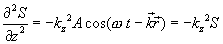შევკრიბოთ სამი უკანასკნელი განტოლება და მივიღებთ
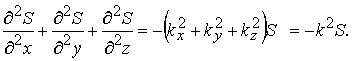
(8.7)-დან გამოდის
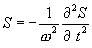
მაშინ
 |
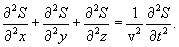(8.8) |
ამ განტოლებას უწოდებენ ტალღურ განტოლებას. ნებისმიერი ფუნქცია, რომელიც აკმაყოფილებს ამ განტოლებას, აღწერს რაღაც ტალღას.