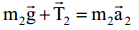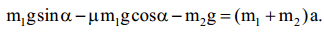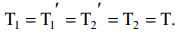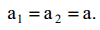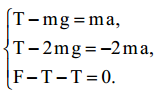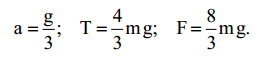განვიხილოთ ცალ-ცალკე თითოეული ტვირთის მოძრაობა. პირველი ტვირთისთვის ნიუტონის მეორე კანონს ვექტორული სახით აქვს ასეთი სახე: 

\(m_{1}\vec{g}+\vec{N}+\vec{T}_{1}+\vec{F}_{fr}=m_{1}\vec{a}_{1}\)

ამ განტოლების პროექტირებით არჩეულ ღერძებზე 0x1 და 0y1, გვაძლ;ევს:

 

 

\(\begin{cases} \right.m_{1}g\sin \alpha -T_{1}-F_{fr}=m_{1}a_{1} \\ -m_{1}g \cos \alpha +N=0 \end{cases}\)                           (1) 

მიღებული სისტემის მეორე განტოლებიდან გვაქვს:

\(N=m_{1}g \cos \alpha\)(2)

ხახუნის ძალისთვის გვექნება

\(F_{fr}=\mu N=\mu m_{1}g \cos \alpha\)           (3)

ჩავსვათ განტ (2) განტოლება (1)-ში, მივიღებთ

ჩავწეროთ ნიუტონის მეორე კანონი მეორე ტვირთვისთვის:

დავაპროექტიროთ უკანასკნელი 0x2, ღერძზე, მივიღებთ

             (4)

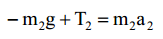
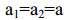
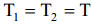
იმის გამო, რომ ძაფი უჭიმვადია: , ხოლო რადგან ჭოჭონაქის მასისა და მასში ხახუნის უგულებელყოფა შეიძლება, ამიტომ: . (3) და (4)-ის შეკრება გვაძლევს:

აქედან აჩქარება

                           (5)

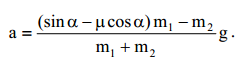
(4)-დან მივიღებთ ძაფის დაჭიმულობის ძალას:

                  (6)

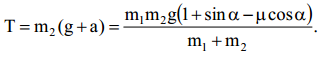
ამოცანის მოცემულობების ჩასმით მივიღებთ:

a  \(\approx\) 1,37მ/წმ2:  T \(\approx\) 13,4ნ.

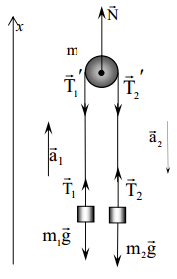
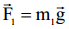
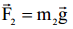
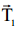
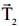
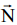
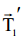
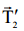
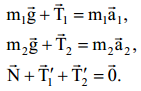
თითოეულ გირაზე მოქმედებს სიმძიმის , ძალა და ძაფის დაჭიმულობის ძალა და . ჭოჭონაქზე ღერძის მხრიდან მოქმედებს რეაქციის ძალა  და მარცხენა მხრიდან  ძაფის დაჭიმულობის ძალა და მარჯვენა მხრიდან  ძაფის დაჭიმულობის ძალა.. ჭოჭონაქი გადატანითად არ გადაადგილდება. ჩავწეროთ მოძრაობის დინამიკის განტოლებები გირებისთვის და ჭოჭონაქისთვის ვექტორული ფორმით: 

                                (1)

რადგან ჭოჭონაქი უწონოა და ძაფი უწონოა და უჭიმვადია, ამიტომ დაჭიმულობა სრულად გადაეცემა მთელი ძაფის გასწვრივ წერტილიდან წერტილს, ანუ

ამას გარდა, რადგან ძაფი უჭიმვადია, ამიტომ:

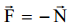
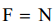
საძებარი დაწოლის ძალა ღერძზე  F დაკავშირებულია ღერძის რეაქციის ძალასთან ნიუტონის მესამე კანონით: ან . ამოცანის პირობის თანახმად m1 = m, ხოლო m2 = 2m. მივმართოთ კოორდინატთა ღერძი X ვერტიკალურად ზევით. მაშინ განტოლება (1) Х ღერძზე მდგენელებში, ყოველივე ზემოთქმულის გათვალისწინებით ჩაიწერება ასე:

ამ სისტემის ამოხსნა მოგვცემს:

ამოცანა 3.1

ჭოჭონაქზე, რომლის მასა და ღერძთან ხახუნი შეიძლება უგულებელიყოს, გადაკიდებულია უჭიმვადი და უწონო ძაფი. ძაფის ბოლებზეებზე ჰკიდია ორი გირი. ნებაზე მიშვებული გირები იწყებენ მოძრაობას. განვსაზღვროთ სისტემის აჩქარება, ძაფების დაჭიმულობის ძალები, ჭოიჭონაქის ღერძზე დაწოლის ძალა, თუ გირების მასებია 1 კგ და 2 კგ. 

 

ამოცანა 3.2

m1=5 კგ მასის ტვირთი, რომელიც უძრავი ღერძის მქონე ჭოჭონაქზე გადადებული უჭიმვადი და უწონო ძაფით დაკავშირებულია მეორე m2 = 1,2 კგ მასის მქონე ტვირთთან, მოძრაობს ქვემოთ დახრილ სიბრტყეზე. ვიპოვნოთ ძაფის დაჭიმულობის ძალა და ტვირთების აჩქარება, თუ ხახუნის კოეფიციენტი პირველ ტვირთსა და სიბრტყეს შორის  \(\mu\)= 0,1. სიბრტყის დახრის კუთხე ჰორიზონტთან ადგენს  \(\alpha\)=30°. ჭოჭონაქის მასა და ხახუნი ულულებელვყოთ.  

 

ამოცანა 3.3

დიდი სიმაღლიდან ვარდნილი სხეულის \(უ\)\(u\) შემდგარი სოჩქარე (რადგან ჰაერის ხახუნის ძალა სიჩქარის ზრდასთან ერთად იზრდება ამიტომ დგება სიჩქარე, როცა ჰაერის წინააღმდეგობის ძალა აწონასწორებს მიზიდულობის ძალას და ამ მომენტიდან სხეული ამ შემდგარი მუდმივი სიჩქარით აგრძელებს მოძრაობას) არის 80 მ/წმ. განვსაზღვროთ დრო, როცა სიჩქარე აღწევს შემდგარი სიჩქარის ნახევარს. ჰაერის წინაღობის ძალა ჩავთვალოთ სხეულის სიჩქარის პროპორციული. თავისუფალი ვარდნის აჩქარება იყოს 9,8 მ/წმ2 .

 

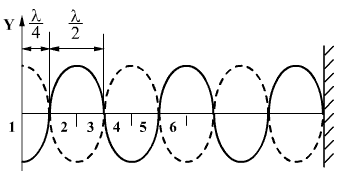
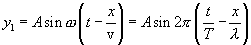
როცა ორი ერთნაირი ტალღა ტოლი ამპლიტუდებითა და პერიოდებით ვრცელდებიან ერთმანეთის შემხვედრად, მაშინ მათი ზედდებისას წარმოიქმნება მდგარი ტალღები. მდგარი ტალღები შეიძლება წარმოიქმნას წინააღმდეგობიდან არეკვლისას. ვთქვათ, გამომსხივებელი აგზავნის ტალღას წინააღმდეგობისკენ (დაცემული ტალღა). წინააღმდეგობისგან არეკლილი ტალღა დაედება დაცემულ ტალღას. მდგარი ტალღის განტოლება შეიძლება მივიღოთ დაცემული ტალღის განტოლებისა

და არეკლილი ტალღის განტოლების

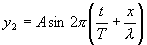
შეკრებით.

არეკლილი ტალღა მოძრაობს დაცემული ტალღის გავრცელების მიმართულების საპირისპირო მიმართულებით, ამიტომ х მანძილს ვიღებთ მინუს ნიშნით. ერთდროულად ორ რხევაში მონაწილე წერტილის წანაცვლება ტოლია ალგებრული ჯამისაა y=y1+y2. არართული გარდაქმნების შემდეგ მივიღებთ

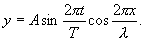(8.15)

ეს მდგარი ტალღის განტოლება განსაზღვრავს ტალღის ნებისმიერი წერტილის წანაცვლებას.

სიდიდე

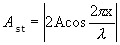(8.16)

არ არის დამოკიდებული დროზე და განსაზღვრავს х კოორდინატის მქონე ნებისმიერი წერტილის ამპლიტუდას. ყოველი წერტილი ასრულებს ჰარმონიულ რხევას Т პერიოდით. Аst ამპლიტუდა ყოველი წერტილისთვის სრულად არის განსაზღვრული, მაგრამ ტალღის ერთი წერტილიდან მეორეზე გადასვლისას იცვლება х-ის მიხედვით. თუ х-ს მივანიჭებთ მნიშვნელობებს 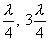 და ა.შ., მაშინ განტოლება (8.16)-ში ჩასმით მივიღებთ  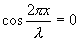. შესაბამისად, ტალღის აღნიშნული წერტილები რჩება უძრავი, რადგან მათი რხევების ამპლიტუდები არის ნული. ამ წერტილებს ეწოდება მდგარი ტალღის კვანძები. წერტილებში, სადაც რხევებს აქვს მაქსიმალური ამპლიტუდა, ეწოდება ანტიკვანძები. მეზობელ კვანძებს ან მეზობელ ანტიკვანძებს შორის მანძილს ეწოდება მდგარი ტალღის სიგრძე და ტოლია

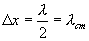
სადაც λ - მსრბოლი ტალღის სიგრძეა.

მდგარ ტალღაში მისი გავრცელების გარემოს ყველა წერტილი, რომელიც მოთავსებულია ორ მეზობელ კვანძს შორის, ირხევა ერთნაირ ფაზაში. გარემოს წერტილები, მოთავსებული კვანძის სხვადასხვა მხარეს, ირხევიან საპირისპირო ფაზებში, მათი ფაზები განსხვავდება \(\pi\)-ით ანუ კვანძზე გადასვლისას რხევის ფაზა ნახტომისებურად იცვლება \(\pi\)-ით. მსრბოლი ტალღებისგან განსხვავებით მდგარ ტალღაში ადგილი არ აქვს ენერგიის გადატანას იმის გამო, რომ მისი შემქმნელი პირდაპირი და უკუ ტალღაებს გადააქვთ ერთნაირი რაოდენობის ენერგია საპირისპირო მიმართულებით.