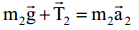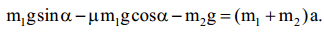\(m_{1}\vec{g}+\vec{N}+\vec{T}_{1}+\vec{F}_{fr}=m_{1}\vec{a}_{1}\)

ამ განტოლების პროექტირებით არჩეულ ღერძებზე 0x₁ და 0y₁, გვაძლ;ევს:

\(\begin{cases} \right.m_{1}g\sin \alpha -T_{1}-F_{fr}=m_{1}a_{1} \\ -m_{1}g \cos \alpha +N=0 \end{cases}\)                           (1) 

მიღებული სისტემის მეორე განტოლებიდან გვაქვს:

\(N=m_{1}g \cos \alpha\)(2)

ხახუნის ძალისთვის გვექნება

\(F_{fr}=\mu N=\mu m_{1}g \cos \alpha\)           (3)

ჩავსვათ განტ (2) განტოლება (1)-ში, მივიღებთ

ჩავწეროთ ნიუტონის მეორე კანონი მეორე ტვირთვისთვის:

დავაპროექტიროთ უკანასკნელი 0x₂, ღერძზე, მივიღებთ

             (4)

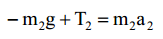
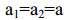
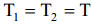
იმის გამო, რომ ძაფი უჭიმვადია: , ხოლო რადგან ჭოჭონაქის მასისა და მასში ხახუნის უგულებელყოფა შეიძლება, ამიტომ: . (3) და (4)-ის შეკრება გვაძლევს:

აქედან აჩქარება

                           (5)

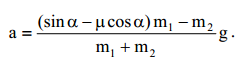
(4)-დან მივიღებთ ძაფის დაჭიმულობის ძალას:

                  (6)

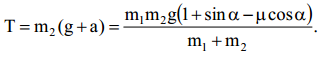
ამოცანის მოცემულობების ჩასმით მივიღებთ:

a  \(\approx\) 1,37მ/წმ²:  T \(\approx\) 13,4ნ.