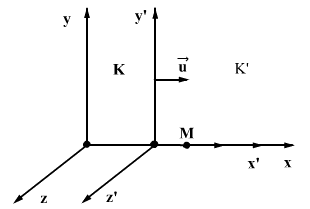
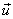 სიჩქარით მოძრავი (K’). М სხეულის კოორდინატები К სისტემაში იყოს x:y:z , ხოლო К’-ში - x’:y’:z’. ეს კოორდინატები ერთმანეთს უკავშირდებიან თანაფარდობებით, რომელთაც ეწოდებათ გალილეის გარდაქმნები
სიჩქარით მოძრავი (K’). М სხეულის კოორდინატები К სისტემაში იყოს x:y:z , ხოლო К’-ში - x’:y’:z’. ეს კოორდინატები ერთმანეთს უკავშირდებიან თანაფარდობებით, რომელთაც ეწოდებათ გალილეის გარდაქმნები
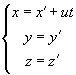
გავაწარმოოთ ეს განტოლებები დროით და გავითვალისწინოთ, რომ 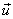 =const, ვიპოვნით თანაფარდობებს სიჩქარეებსა და აჩქარებებს შორის:
=const, ვიპოვნით თანაფარდობებს სიჩქარეებსა და აჩქარებებს შორის:
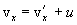 |
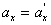 |
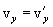 |
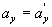 |
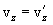 |
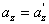 |
ამდენად, თუ К სისტემაში სხეულს აქვს а აჩქარება, მაშინ ასეთივე აჩქარება ექნება მას К’ სისტემაშიც.
ნიუტონის მეორე კანონის თანახმად:
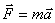
ანუ ნიუტონის მეორე კანონი ორივე სისტემაში ერთნაირია.
როცა 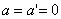 გვაქვს ინერციით მოძრაობა, ამდენად სამართლიანია ნიუტონის პირველი კანონიც, ანუ ჩვენს მიერ განხილული მოძრავი სისტემა არის ინერციული. შესაბამისად, ნიუტონის განტოლებები მატერიალური წერტილისთვის, ასევე მატერიალური წერტილების ნებისმიერი სისტემისთვის ერთნაირია ყველა ინერციულ ათვლის სისტემაში - ინვარიანტულია გალილეის გარდაქმნების მიმართ. ამ შედეგს ეწოდება ფარდობითობის მექანიკური პრინციპი (გალილეის ფარდობითობის პრინციპი) და ფორმულირდება შემდეგნაირად: ჩაკეტილი სისტემის წრფივი და თანაბარი მოძრაობა (რომელიმე ათვლის სისტემის მიმართ) არ მოქმედებს მასში მექანიკური პროცესების მიმდინარეობის კანონზომიერებებზე. შესაბამისად, მექანიკაში ყველა ინერციული სისტემა თანაბარია. ამიტომ თვით სისტემის შიგნით ვერავითარი მექანიკური ცდით ვერ დავადგენთ მოძრაობს სისტემა წრფივად და თანაბრად თუ უძრავია.
გვაქვს ინერციით მოძრაობა, ამდენად სამართლიანია ნიუტონის პირველი კანონიც, ანუ ჩვენს მიერ განხილული მოძრავი სისტემა არის ინერციული. შესაბამისად, ნიუტონის განტოლებები მატერიალური წერტილისთვის, ასევე მატერიალური წერტილების ნებისმიერი სისტემისთვის ერთნაირია ყველა ინერციულ ათვლის სისტემაში - ინვარიანტულია გალილეის გარდაქმნების მიმართ. ამ შედეგს ეწოდება ფარდობითობის მექანიკური პრინციპი (გალილეის ფარდობითობის პრინციპი) და ფორმულირდება შემდეგნაირად: ჩაკეტილი სისტემის წრფივი და თანაბარი მოძრაობა (რომელიმე ათვლის სისტემის მიმართ) არ მოქმედებს მასში მექანიკური პროცესების მიმდინარეობის კანონზომიერებებზე. შესაბამისად, მექანიკაში ყველა ინერციული სისტემა თანაბარია. ამიტომ თვით სისტემის შიგნით ვერავითარი მექანიკური ცდით ვერ დავადგენთ მოძრაობს სისტემა წრფივად და თანაბრად თუ უძრავია.
ნიუტონის მესამე კანონი შემდეგნაირად ფორმულირდება:
ორი მატერიალური წერტილი მოქმედებენ ერთმანეთზე ძალებით, რომლებიც სიდიდეებით ტოლია ერთმანეთის და ურთიერთსაპირისპიროდ არიან მიმართულნი იმ წრფის გასწვრივ, რომელიც აერთებს ამ წერტილებს:
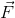 12= 12=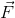 21 21 |
(3.4) |
უნდა აღინიშნოს, რომ ძალები 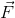 12 და
12 და 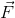 21 მოდებულია სხვადასხვა სხეულზე და ამიტომ ერთმანეთს არ აწონასწორებენ.
21 მოდებულია სხვადასხვა სხეულზე და ამიტომ ერთმანეთს არ აწონასწორებენ.
თუ მატერიალურ წერტილზე მოქმედებს რამდენიმე ძალა, მაშინ
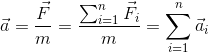 |
(3.3) |
სადაც  არის მატერიალური წერტილის აჩქარება, რომელიც გამოწვეულია ერთი
არის მატერიალური წერტილის აჩქარება, რომელიც გამოწვეულია ერთი 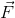 i ძალით. ასე რომ, თუ სხეულზე მოქმედებს რამდენიმე ძალა, მაშინ თითოეული მათქანი ანიჭებს მატერიალურ წერტილს ისეთ აჩქარებას, როგორსაც ის მიანიჭებდა სხვა ძალების ზემოქმედების არარსებობის შემთხვევაში. ამას ეწოდება ძალების ქმედების დამოუკიდებლობის პრინციპი.
i ძალით. ასე რომ, თუ სხეულზე მოქმედებს რამდენიმე ძალა, მაშინ თითოეული მათქანი ანიჭებს მატერიალურ წერტილს ისეთ აჩქარებას, როგორსაც ის მიანიჭებდა სხვა ძალების ზემოქმედების არარსებობის შემთხვევაში. ამას ეწოდება ძალების ქმედების დამოუკიდებლობის პრინციპი.
ცდა აჩვენებს, რომ  ძალის მოქმედებით თავისუფალი სხეული იცვლის გადატანითი მოძრაობის სიჩქარეს და იძენს
ძალის მოქმედებით თავისუფალი სხეული იცვლის გადატანითი მოძრაობის სიჩქარეს და იძენს  აჩქარებას. ამასთან სხეულის აჩქარება პირდაპირპროპორციულია გამომწვევი ძალისა და აქვს ამ ძალის მიმართულება:
აჩქარებას. ამასთან სხეულის აჩქარება პირდაპირპროპორციულია გამომწვევი ძალისა და აქვს ამ ძალის მიმართულება:
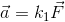
სადაც k1 არის დადებითი პროპორციულობის კოეფიციენტი, რომელიც მუდმივია ყოველი კონკრეტული სხეულისთვის.
აჩქარების სიდიდე, რომელიც შეიძინა სხეულმა 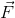 ძალის ზემოქმედებით, დამოკიდებულია სხეულზე, რომელზეც მოქმედებს ძალა. რადგან დიდ სხეულებს უფრო ძნელად მიენიჭება აჩქარება ვიდრე მცირეებს, მიღებულია ძალასა და აჩქარებას შორის პროპორციულობა გამოვსახოთ შემდეგი ფორმით:
ძალის ზემოქმედებით, დამოკიდებულია სხეულზე, რომელზეც მოქმედებს ძალა. რადგან დიდ სხეულებს უფრო ძნელად მიენიჭება აჩქარება ვიდრე მცირეებს, მიღებულია ძალასა და აჩქარებას შორის პროპორციულობა გამოვსახოთ შემდეგი ფორმით:
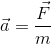 |
(3.2) |
m პროპორციულობის კოეფიციენტი დამოკიდებულია საგანზე. მისი სიდიდე იზრდება სხეულის ზომების ზრდით, თუ ისინი ერთგვაროვანნი არიან. m მუდმივას უწოდებენ სხეულის მასას. მასა წარმოადგენს სხეულის ინერტულობის საზომს გადატანითი მოძრაობისას. რაც ნაკლებია სხეულის ინერტულობა, მით მეტი აჩქარება უნდა შეიძინოს მან რაღაც გარკვეული ძალის ზემოქმედების შედეგად. ასე რომ, ნიუტონის მეორე კანონი შეიძლება ასე ჩამოვაყალიბოთ: სხეულის აჩქარება პირდაპირპროპორციულია მისი გამომწვევი ძალისა, ემთხვევა მას მიმართულებით და უკუპროპორციულია სხეულის მასისა.


