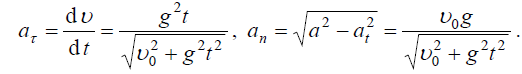
 სიჩქარე ვერ ჩაითვლება მთელი სხე ულის მახასიათებლად.
სიჩქარე ვერ ჩაითვლება მთელი სხე ულის მახასიათებლად.
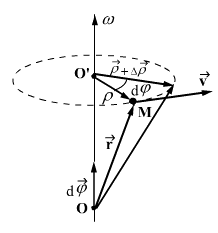
ვთქვათ წერტილი О არის სხეულის ბრუნვის ცენტრი, ხოლო ОО' არის ბრუნვის უძრავი (ან მყისიერი) ღერძი.
ნებისმიერი М წერტილის მდებარეობა მოიცემა О ცენტრიდან გავლებული 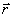 რადიუს-ვექტორის მეშვეობით. ნახაზიდან ჩანს, რომ:
რადიუს-ვექტორის მეშვეობით. ნახაზიდან ჩანს, რომ:
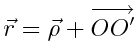 ,
,
სადაც 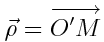 არის რადიუს-ვექტორი, გავლებული იმ წრეწირის ცენტრამდე, რომელზეც მოძრაობს М წერტილი. მცირე დროში
არის რადიუს-ვექტორი, გავლებული იმ წრეწირის ცენტრამდე, რომელზეც მოძრაობს М წერტილი. მცირე დროში 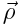 ვექტორი შემობრუნდება ОО' ღერძის პერპენდიკულარულ სიბრტყეში მცირე
ვექტორი შემობრუნდება ОО' ღერძის პერპენდიკულარულ სიბრტყეში მცირე 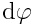 კუთხით. იგივე კუთხით შემობრუნდება
კუთხით. იგივე კუთხით შემობრუნდება 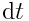 დროში სხეულის ნებისმიერი სხვა წერტილი, რადგან წინააღმდეგ შემთხვევაში მანძილები ამ წერტილებს შორის უნდა შეცვლილიყო. ამდაგვარად, შემობრუნების კუთხე ახასიათებს მთელ მბრუნავ სხეულს დროის მცირე შუალედში. მოსახერხებელია შემოვიღოთ სხეულის ელემენტარული (მცირე) შემობრუნების
დროში სხეულის ნებისმიერი სხვა წერტილი, რადგან წინააღმდეგ შემთხვევაში მანძილები ამ წერტილებს შორის უნდა შეცვლილიყო. ამდაგვარად, შემობრუნების კუთხე ახასიათებს მთელ მბრუნავ სხეულს დროის მცირე შუალედში. მოსახერხებელია შემოვიღოთ სხეულის ელემენტარული (მცირე) შემობრუნების 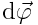 ვექტორი, რომელიც რიცხობრივად უდრის
ვექტორი, რომელიც რიცხობრივად უდრის 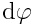 -ს და მიმართულია მყისიერი ღერძის გასწვრივ ისე, რომ მისი ბოლოდან სხეულის ბრუნვა საათის ისრის საწინააღმდეგოდ გამოჩნდეს.
-ს და მიმართულია მყისიერი ღერძის გასწვრივ ისე, რომ მისი ბოლოდან სხეულის ბრუნვა საათის ისრის საწინააღმდეგოდ გამოჩნდეს.
თუ აბსოლუტურად მყარი სხეულის მოძრაობისას მისი А და В წერტილები რჩება უძრავი, მაშინ სხეულის ნებისმიერი С წერტილიც, რომელიც მდებარეობს АВ წრფეზე, ასევე დარჩება უძრავი. წინააღმდეგ შემთხვევაში მანძილები АС და ВС უნდა იცვლებოდნენ, რაც შეეწინააღმდეგებოდა აბსოლუტური მყარი სხეულის დაშვებას. ამიტომ მყარი სხეულის მოძრაობას, რომლის დროსაც ორი მისი А და В წერტილი რჩება უძრავი, უწოდებენ მყარი სხეულის ბრუნვას უძრავი ღერძის გარშემო, ხოლო უძრავ АВ წრფეს უწოდებენ ბრუნვის ღერძს.
განვიხილოთ სხეულის ნებისმიერი М წერტილი, რომელიც არ ძევს АВ ბრუნვის ღერძზე. სხეულის ბრუნვისას მანძილები МА და МВ და М წერტილიდან ბრუნვის ღერძამდე ρ მანძილი უნდა დარჩნენ უცვლელნი.. ამდაგვარად, უძრავი ღერძის ირგვლივ მბრუნავი სხეულის ყველა წერტილი შემოწერენ წრეწირებს, რომელთა ცენტრებიც მდებარეობენ ბრუნვის ღერძზე. აბსოლუტურად მყარი სხეულის ბრუნვას, უძრავი წერტილის ირგვლივ, უწოდებენ სხეულის ბრუნვას უძრავი წერტილის - ბრუნვის ცენტრის ირგვლივ. აბსოლუტურად მყარი სხეულის ასეთი მოძრაობა დროის ნებისმიერ მომენტში შეიძლება განვიხილოთ, როგორც ბრუნვა რაღაც ღერძის ირგვლივ, რომელიც გადის ბრუნვის ცენტრზე და ამ ღერძს უწოდებენ ბრუნვის მყისიერ ღერძს. მყისიერი ღერძის მდებარეობა უძრავი ათვლის სისტემის მიმართ და თვით სხეულის მიმართ დროთა განმავლობაში შეიძლება იცვლებოდეს.
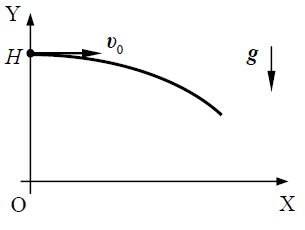
II. საწყისი პირობებისა და არჩეული ათვლის სისტემის თანახმად
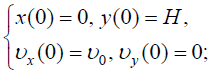
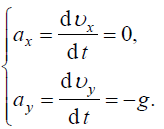
III. სიჩქარისა და რადიუსვექტორის მდგენელებისთვის საწყისი პირობების გათვალისწინებით გვაქვს:
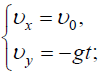
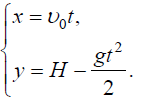
ტრაექტორიის განტოლებას მივიღებთ (4) t დროის გამორიცხვით:
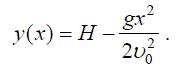
სიჩქარის მოდული იქნება:

აჩქარების მოდული:
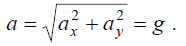
აჩქარების მდგენელები:
(8)
სიმრუდის რადიუსი:
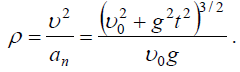
აღსანიშნავია, რომ ამოხსნაში მოყვანილი ყველა ფორმულა სამართლიანია დროის საწყისი მომენტიდან სხეულის დედამიწაზე დაცემამდე. ადვილია მოვძებნოთ ეს მომენტი განტ. (4)-დან თუ y კოორდინატას გავუტოლებთ ნულს:
 . (1.49)
. (1.49)
მივყვეთ მატერიალური წერტილის კინემატიკის ამოცანების ამოხსნის ზოგად სქემას.
I. ამოცანის პირობის თანახმად მოძრაობა მიმდინარეობს XY სიბრტყეში, რომელიც შექმნილია კოორდინატთა X და Y ღერძებით და მათი მიმართულებები განისაზღვრება შესაბამისად  და
და 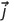 ორტებით.
ორტებით.
II. ჩავწეროთ არჩეულ კოორდინატთა სისტემაში საწყისი პირობები და სხეულის სიჩქარის ცვლილების კანონი მდგენელებში:
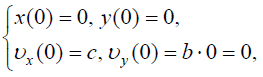
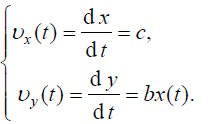
III. (2) დიფერენციალური განტოლებები, (1) საწყის პირობების გათვალისწინებით საშუალებას იძლევა მოვზებნოთ მატერიალური წერტილის მოძრაობის კანონი კოორდინატთა ღერძებზე პროექციებით და რადიუს ვექტორის დროზე დამოკიდებულება:
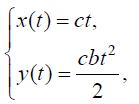
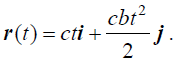
ნაპოვნი (4) გამოსახულების გამოყენებით განვსაზღვროთ სიჩქარისა და აჩქარების ცვლილების კანონები:
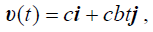
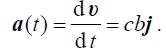
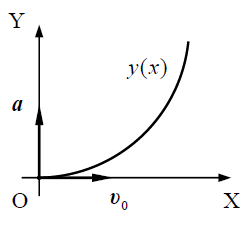
ტრაექტორიის განტოლება მოიძებნება მატერიალური წერტილის მოძრაობის კანონიდან (3)-დან t დროის გამორიცხვით:
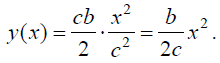
სიჩქარის მოდული განისაზღვრება ასე:
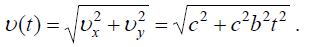
აჩქარების ტანგენციალური და ნორმალური მდგენელები შესაბამისად:
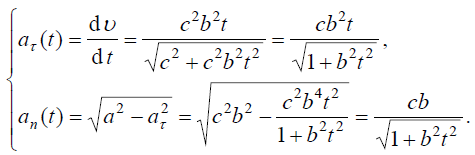
ტრაექტორიის სიმრუდის რადიუსი ასეთია:
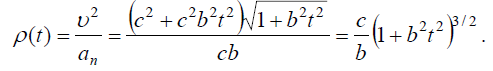
სიჩქარესა და აქარებას შორის კუთხე იქნება: