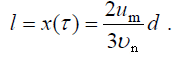I. ავირჩიოთ ათვლის სისტემა ისე, როგორც ნახაზზეა მითითებული.
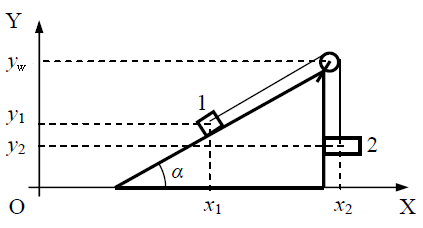
II. გამოვსახოთ ძაფის სიგრძე განსახილველ სხეულთა სისტემის სხვადასხვა წერტილის ვერტიკალური კოორდინატებით:
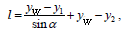
სადაც yw – ჭოჭონაკის კოორდინატია, რომელიც მოძრაობის პროცესში არ იცვლება.
ძაფის დახრილი უბნის სიგრძეს თუ გამოვსახავთ სხეულთა სისტემის ჰორიზონტული კოორდინატებით, მაშინ ძაფის სიგრძის გამოსახულება მიიღებს სახეს:
. 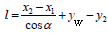
III. ორჯერ გავაწარმოოთ (1) და (2) დროით და გავითვალისწინოთ რომ 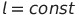 და
და 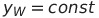 , მივიღებთ, განტოლებებს სისტემის სხეულთა აჩქარებებისთვის:
, მივიღებთ, განტოლებებს სისტემის სხეულთა აჩქარებებისთვის:
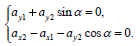
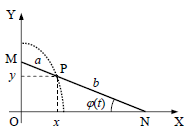
ავირჩიოთ და გამოვსახოთ დეკარტის კოორდინატთა სისტემა ისე, რომ მისი ღერძები ემთხვეოდეს MON კუთხეს
ამოცანის პირობის თანახმად ჩავთვალოთ ძელაკი აბსოლუტურად მყარად. შესაბამისად მისი მდებარეობა დროის ნებისმიერ t მომენტში ცალსახად მოიცემა OX ღერძსა და MN ძელაკს შორის \(\varphi \left ( t \right )\) კუთხით.
II. ჩავწეროთ P წერტილის მოძრაობის კანონი კოორდინატული ფორმით:
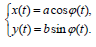
გამოვრიცხოთ აქედან დრო და მივიღებთ P წერტილის ტრაექტორიის განტოლებას. ამისთვის გარდავქმნათ (1) ასე:
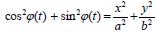
შედეგად საძებნი ტრაექტორიის განტოლება ასე გამოიყურება:
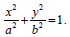
განტოლება (3) წარმოადგენს ელიფსის განტოლებას, რომლის ნახევარღერძებია a და b. როცა a = b, ელიფსი გადაგვარდება წრეწირად.
I. წარმოვადგინოთ ნახაზი წვეთისთვის ტრამვაის დამუხრუჭების დასაწყისში
ავირჩიოთ დედამიწასთან დაკავშირებული XY კოორდინატთა სისტემა ისე, რომ X იყოს მიმართული ჰორიზონტალურად აჩქარების გასწვრივ, ხოლო Y – ვერტიკალურად ქვევით. ავირჩიოთ ასევე მეორე - ტრამვაის ფანჯარასთან მიმაგრებული კოორდინატთა სისტემა X′Y′ ისე, რომ მისი ღერძები X′ და Y′ იყოს თანამიმართული X და Y ღერძებთან შესაბამისად. ორივე სისტემაში დრო აითვლება დამუხრუჭების დაწყების მომენტიდან. წვიმის წვეთს ჩავთვლით მატერიალურ წერტილად, რომლის მდებარეობა საწყის მომენტში ემთხვევა X′Y′ კოორდინატთა სისტემის სათავეს.
II. მოძრაობის სუპერპოზიციის პრინციპის გამოყენებით ჩავწეროთ წვეთის სიჩქარე და აჩქარება ტრამვაის მინის მიმართ ( X′Y′ კოორდინატთა სისტემა):
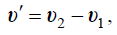
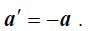
არჩეულ სისტემასთან შესაბამისობაში ჩავწეროთ წვეთის საწყისი პირობები:

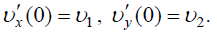
III. დიფერენციალური განტოლებები (1) და (2), (3) და(4) საწყისი პირობების გათვალისწინებით საშუალებას გვაძლევს განვსაზღვროთ წვეთის მოძრაობის განტოლებები კოორდინატთა ღერძებზე მდგენელებით:
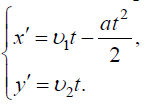
აქედან დროის გამორიცხვით მივიღებთ წვეთის ტრაექტორიის განტოლებას:
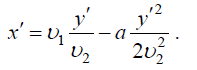
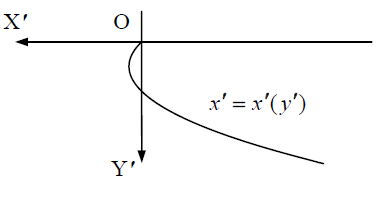
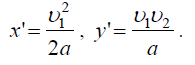
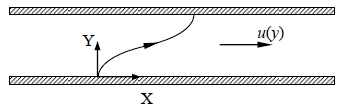
I. ვირჩევთ დეკარტის კოორდინატთა სისტემას, მიმაგრებულს მდინარის ნაპირზე სათავით ნავის მდინარეში შეცურვის ადგილზე. სისტემის ღერძები და მდინარის სიჩქარის მიმართულება ნახაზზეა გამოსახული.
ამოცანის ამოხსნისას ნავს მივიჩნევთ მატერიალურ წერტილად, ხოლო მდინარის ნაპირებს ურთიერთპარალელურად.
II. ამოცანის პირობის თანახმად ნავისთვის საწყისი პირობები არის
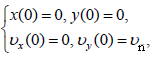
სადაც 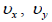
მოძრაობის სუპერპოზიციის პრინციპის თანახმად, დროის ნებისმიერ მომენტში 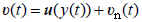
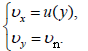
ამოცანის პირობის თანახმად მდინარის სიჩქარე პარაბოლურად არის დამოკიდებული ნაპირიდან დაშირებაზე ამიტომ შეგვიძლია ჩავწეროთ,
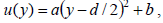
სადაც a და b – მუდმივი სიდიდეებია. -ს განსაზღვრისთვის გამოვიყენებთ ამოცანის იმ პირობას, რომ მდინარის შუაში დინების სიჩქარე მაქსიმალურია ანუ:
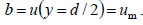
0-ში საწყისი პირობით გვაქვს
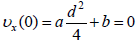
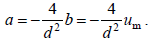
III. განტოლებათა სისტემა (2), განტოებების (3) – (5) -ის გამოყენებით მიიღებს სახეს:
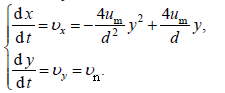
(1) საწყისი პირობების გათვალისწინებით და განტოლებების (6) ინტეგრირებით მივიღებთ მოძრაობის კანონს ანუ კოორდინატების დროზე დამოკიდებულებას:
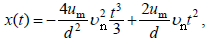
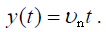
ტრაექტორიის განტოლების მისაღებად განტოლებებიდან (7) და (8) გამოვრიცხოთ დრო და მივიღებთ:
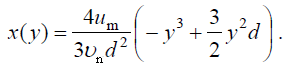
რადგან ნაპირთან მიყუდებისას 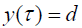
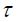
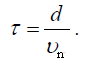
შესაბამისად წატაცების