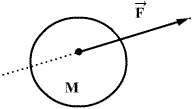
ძალის ქვეშ ვგულისხმობთ ფიზიკურ სიდიდეს, რომელიც წარმოადგენს სხეულზე სხვა სხეულების მექანიკური ზემოქმედების ზომას.
სხეულზე მოდებული ძალა სრულად არის განსაზღვრული, თუ მითითებულია მისი რიცხვითი მნიშვნელობა, მოქმედების მიმართულება და მოდების წერტილი М. მოდების წერტილიდან ძალის მიმართულებით გავლებულ წრფეს, ძალის მოქმედების წრფეს უწოდებენ. ორ ძალას ეწოდება რიცხობრივად ტოლი და ურთიერთსაპირისპირო, თუ სხეულის ერთსადაიმავე წერტილში მათი მოდება არ იწვევს სხეულის მექანიკური მოძრაობის ცვლილებას. კერძოდ, თუ ასეთი ძალების მოდებამდე სხეული უძრავი იყო, მაშინ მათი მოდების შემდეგაც უძრავი დარჩება. ამიტომ ამბობენ, ორი რიცხობრივად ტოლი და საპირისპიროდ მიმართული ძალა, რომლებიც სხეულის ერთსადაიმავე წერტილშია მოდებული ერთმანეთს აწონასწორებენ.
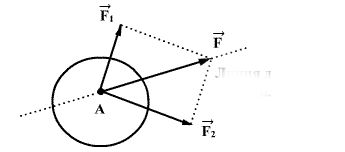
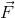 ძალით, რომელიც ტოლია მათი გეომეტრიული ჯამისა
ძალით, რომელიც ტოლია მათი გეომეტრიული ჯამისა
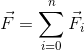 |
(3.1) |
და მოდებულია იმავე წერტილში. ამ ძალას ტოლქმედს უწოდებენ. აბსოლუტურად მყარ სხეულზე ძალის ზემოქმედება არ იცვლება მისი მოქმედების წრფის გასწვრივ გადატანით.
ნიუტონის პირველი კანონი ამბობს: ყოველი სხეული ინარჩუნებს უძრაობის ან თანაბარი წრფივი მოძრაობის მდგომარეობას მანამ, სანამ სხვა სხეულებისგან ზემოქმედება არ აიძულებს შეიცვალოს ეს მდგომარეობა. ნიუტონის პირველი კანონი აჩვენებს, რომ უძრაობის ან თანაბარი წრფივი მოძრაობის მდგომარეობა არ მოითხოვს გარედან ზემოქმედებას. ამაში ვლინდება სხეულების განსაკუთრებული დინამიური თვისება, ინერტულობა. შესაბამისად ნიუტონის პირველ კანონს უწოდებენ ინერციის კანონს, ხოლო სხეულების სხვა სხეულების მხრიდან ზემოქმედებისგან თავისუფალ მოძრაობას - ინერციით მოძრაობას.
ცდა აჩვენებს, რომ ნიუტონის პირველი კანონი არ სრულდება ათვლის ყველა სისტემის მიმართ. ათვლის სიტემებს, რომელთა მიმართაც სრულდება ინერციის კანონი, ეწოდება ათვლის ინერციული სისტემები. ანუ, ეს ისეთი ათვლის სისტემებია, რომელთა მიმართაც მატერიალური წერტილი, რომელზეც არ ზემოქმედებენ სხვა სხეულები, ან უძრავია, ან მოძრაობს წრფივად და თანაბრად.
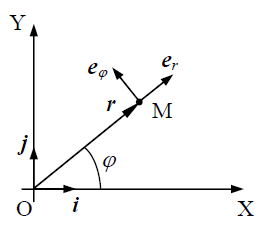
აღსანიშნავია, რომ მატერიალური წერტილის მოძრაობისას პოლარული სისტემის ორტები იცვლის ორიენტაციას, მაშინ როცა დეკარტის სისტემის ორტები არ იცვლის მიმართულებას.
პოლარულ სისტემაში მოცემული მატერიალური წერტილის მოძრაობის კანონი ჩავწეროთ დეკარტის კოორდინატთა სისტემაში:
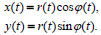
(1)-ის გაწარმოებით მივიღებთ:
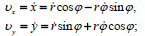
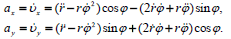
მეთოდი 1.
პოლარულ სისტემაში სიჩქარე და აჩქარება ჩაიწერება ასე:
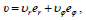
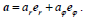
შესაბამისად, მატერიალური წერტილის სიჩქარისა და აჩქარების მდგენელები მიმართულებებზე, რომელიც მოცემულია არჩეული სისტემების ორტებით, დაკავშირებულია შემდეგი თანაფარდობებით:
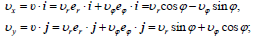
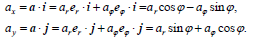
შევადაროთ გამოსახულებები (1) და (6), ასევე (2) და (7), მივიღებთ სიჩქარისა და აჩქარებიის სასურველ პროექციებს პოლარულ კოორდინატთა სისტემაში:
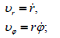
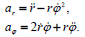
მეთოდი 2.
ჩავწეროთ მატერიალური წერტილის რადიუს-ვექტორი პოლარულ კოორდინატებში:

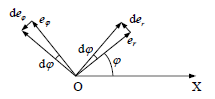

ახლა იმავე კოორდინატთა სისტემაში წერტილის სიჩქარისა და აჩქარების მოსაძებნად საჭიროა რადიუს-ვექტორი (10) გავაწარმოოთ დროით (11)-ის გათვალისწინებით.

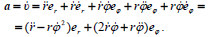
(12) და (13)-ის შესაბამისად მატერიალური წერტილის სიჩქარისა და აჩქარების საძებნი მდგენელები პოლარულ კოორდინატებში იქნება
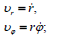
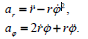
როგორც ვხედავთ ამოხსნის ორივე მეთოდი ერთდაიგივე შედეგს გვაძლევს.
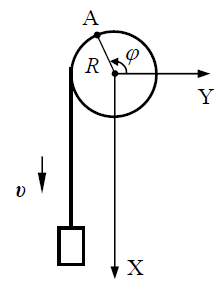
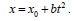
რადგან ამოცანაში სხვაგვარად არ არის დათქმული ჩავთვალოთ თოკი უჭიმვადად და კინემატიკური ბმის განტოლება იქნება:

(1)-დან გვექნება
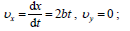
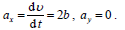
ლილვის ზედაპირის წერტილები ასრულებენ არათანაბარ წრიულ მოძრაობას ამასთან მათი სიჩქარის მოდული (რადგან ძაფი უჭიმვადია და არ სრიალებს ზედაპირზე) დროის ნებისმიერ მომენტში ტოლია ტვირთის სიჩქარის მოდულისა, ამიტომ შეგვიძლია დავწეროთ
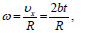
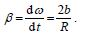
რადგან ტვირთის აჩქარების მდგენელი X ღერძზე ტოლია ლილვის ზედაპირის წერტილების აჩქარების ტანგენციალური მდგენელის, ამიტომ:
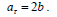
აჩქარების ნორმალური მდგენელი იქნება:
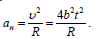
სრული აჩქარების მოდული:
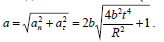
ლილვის ზედაპირის ნებისმიერი A წერტილის მოძრაობის განტოლება ჩავწეროთ პოლარულ კოორდინატთა სისტემაში:
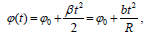
სადაც 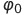 არის A წერტილის საწყისი კუთხური კოორდინატა.
არის A წერტილის საწყისი კუთხური კოორდინატა.