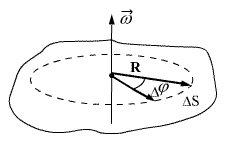
მბრუნავი სხეულის სხვადასხვა წერტილებს აქვთ განსხვავებული სიჩქარეები. ყოველი წერტილის სიჩქარე, მიმართულია რა შესაბამისი წრეწირის მხების გასწვრივ, უწყვეტად იცვლის მიმართულებას.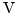 
სიჩქარის სიდიდე განისაზღვრება სხეულის \(\omega\) ბრუნვის სიჩქარითა და წერტილის ბრუნვის ღერძიდან R დაშორებით. ვთქვათ \(\Delta t\) მცირე დროის განმავლობაში სხეული შემობრუნდა 
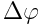კუთხით. ღერძიდან R მანძილით დაშორებული წერტილი გაივლის გზას
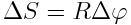
განსაზღვრების თანახმად წერტილის წრფივი სიჩქარე არის
 |
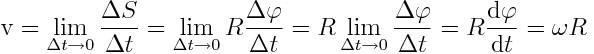(2.6) |
ვიპოვნოთ მბრუნავი სხეულის წირითი აჩქარებები. ნორმალური აჩქარება:
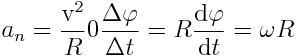
ჩავსვათ სიჩქარის მნიშვნელობა (2.6)-დან, გვექნება:
 |
(2.7) |
ტანგენციური აჩქარება
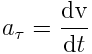
გამოვიყენოთ ისევ გამოსახულება (2.6) და მივიღებთ:
 |
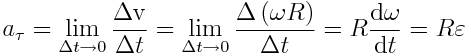(2.8) |
ამდაგვარად, როგორც ნორმალური, ისე ტანგენციური აჩქარება იზრდება წრფივად წერტილის ღერძთან დაშორების მიხედვით.
არათანაბარი ბრუნვისას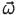 
არ რჩება მუდმივი. სიდიდეს, რომელიც ახასიათებს კუთხური სიჩქარის ცვლილების სისწრაფეს, ეწოდება კუთხური აჩქარება და ტოლია:
 |
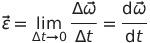(2.5) |
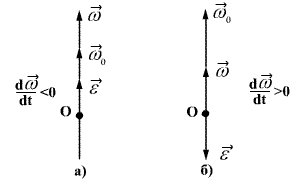
სხეულის უძრავი ღერძის ირგვლივ ბრუნვის შემთხვევაში 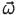ვექტორის ცვლილება განპირობებულია მხოლოდ მისი რიცხვითი მნიშვნელობის ცვლილებით. ამასთან 
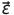კუთხური აჩქარების ვექტორი მიმართულია ბრუნვის ღერძის გასწვრივ იგივე მიმართულებით, რაც აქვს 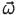აჩქარებული მოძრაობისას 
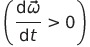და შენელებული მოძრაობისას 
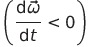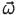კი -ს საპირისპირო მიმართულება აქვს.
დროს, რომელშიც სხეული ასრულებს ერთ სრულ შემობრუნებას, ანუ შემობრუნდება 
კუთხით, ეწოდება ბრუნვის პერიოდი. რადგან 
დროის შუალედს შეესაბამება 
შემობრუნების კუთხე, ამიტომ
,
საიდანაც ვღებულობთ
 |
(2.2) |
ერთეულოვან დროში 
ბრუნვათა რიცხვი აშკარაა, რომ უდრის:
 |
(2.3) |
აქედან ვღებულობთ, რომ კუთხური სიჩქარე
 |
(2.4) |
ვექტორულ სიდიდეს
 |
(2.1) |
ეწოდება სხეულის კუთხური სიჩქარე.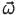 
ვექტორი მიმართულია ბრუნვის მყისი ღერძის გასწვრივ მარჯვენა ბურღის წესით განსაზღვრულ მხარეს, ანუ ისევე, როგორც ელემენტარული შემობრუნების ვექტორი 
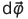. კუთხური სიჩქარის მოდული უდრის 
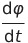-ს. ბრუნვას მუდმივი კუთხური სიჩქარით ეწოდება თანაბარი, ამასთან:
,
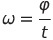ანუ, თანაბარი ბრუნვისას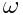 
გვიჩვენებს ერთეულოვან დროში რა კუთხით შემობრუნდება სხეული.