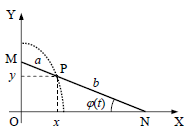
ავირჩიოთ და გამოვსახოთ დეკარტის კოორდინატთა სისტემა ისე, რომ მისი ღერძები ემთხვეოდეს MON კუთხეს

ამოცანის პირობის თანახმად ჩავთვალოთ ძელაკი აბსოლუტურად მყარად. შესაბამისად მისი მდებარეობა დროის ნებისმიერ t მომენტში ცალსახად მოიცემა OX ღერძსა და MN ძელაკს შორის  \(\varphi \left ( t \right )\) კუთხით.

II. ჩავწეროთ P წერტილის მოძრაობის კანონი კოორდინატული ფორმით:

                       (1)

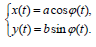
გამოვრიცხოთ აქედან დრო და მივიღებთ P წერტილის ტრაექტორიის განტოლებას. ამისთვის გარდავქმნათ (1) ასე:

     (2)

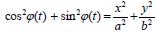
შედეგად საძებნი ტრაექტორიის განტოლება ასე გამოიყურება:

                             (3)

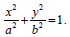
განტოლება (3) წარმოადგენს ელიფსის განტოლებას, რომლის ნახევარღერძებია a და b. როცა a = b, ელიფსი გადაგვარდება წრეწირად.