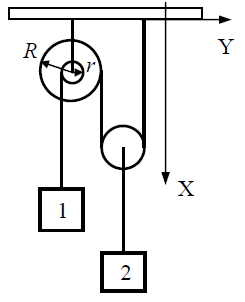
ვთვლით 1 და 2 სხეულებს მატერიალურ წერტილებად, ძავფს კი უჭიმვადად. ძაფები ჭოჭონაქების მიმართ არ სრიალებენ.
II. ვთქვათ დროის მცირე Δt ინტერვალში პირველი სხეულის კოორდინატის ცვლილება არის  Δx₁ (სიცხადისთვის ვთქვათ იგი ეშვება). რადგან ძაფი უჭიმვადია, ამიტომ r რადიუსის ცილინდრის შემობრუნების \(\Delta \varphi\) კუთხე უკავშირდება  Δx₁-ს ასე

\(\Delta x_{1}=r\Delta \varphi\)           (1)

ამასთან R რადიუსის ცილინდრი შემობრუნდება ამავე კუთხით, ხოლო ძაფის სიგრძე, რომელიც მასზეა მოთავსებული და რომელზეც ჰკიდია სხეული 2 შეიცვლება სიდიდით:

\(\Delta l=-R\Delta \varphi\)         (2)

მეორე ჭოჭონაქის ცენტრის და ესეიგი მეორე სხეულის კოორდინატის ცვლილება იქნება:

     (3)

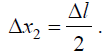
III. განტოლებათა (1) – (3) სისტემის ამოხსნა გვაძლევს ორი სხეულის კოორდინატთა ცვლილებებს შორის კავშირის განტოლებას:

\(\Delta x_{2}=-\frac{R}{r}\frac{\Delta x_{1}}{2}\)        (4)

ამ განტოლების მარჯვენა და მარცხენა მხარეები გავყოთ დროის მცირე შუალედზე და \(\Delta t\rightarrow 0\) ზღვარზ ე გადასვლით მივღებთ სხეულების სიჩქარეებს შორის კავშირის განტოლებას:

\(v_{2}=-\frac{R}{r}\frac{v_{1}}{2}\)         (5)

მიღებული თანაფარდობის დროით გაწარმოებით მივიღებთ სხეულების აჩქარებებს შორის კავშირს:

\(a_{2}=-\frac{R}{r}\frac{a_{1}}{2}\)         (6)